Контрольная по мат.стату. Контрольная работа 2 Задание в результате наблюдений некоторый признак (случайная величина) X принял ряд значений. Требуется
 Скачать 477 Kb. Скачать 477 Kb.
|
|
Контрольная работа № 2 Задание 1. В результате наблюдений некоторый признак (случайная величина) X принял ряд значений. Требуется: 1) найти размах выборки; 2) составить дискретный вариационный ряд с соответствующими частотами и относительными частотами; 3) построить полигон частот и относительных частот; 4) построить эмпирическую функцию распределения F*(х) и кумуляту; 5) найти моду M0 и медиану Ml; 6) вычислить выборочную среднюю ( 7) вычислить коэффициент вариации; 8) оценить с надежностью γ = 0,95 и γ = 0,99 математическое ожидание, дисперсию и СКО нормально распределенною признака генеральной совокупности с помощью доверительных интервалов. 9,9,14,11,11,12,12,13,13,10,10,10,9,14,14,11,11,9,11,10,10,10,12,10,10 Решение: 1) Размах выборки: 2) Запишем вариационный ряд: 9,9,9,9,10,10,10,10,10,10,10,10,11,11,11,11,11,12,12,12,13,13,14,14,14. Cоставим дискретный вариационный ряд с соответствующими частотами и относительными частотами:
3) Построим полигон частот и относительных частот. 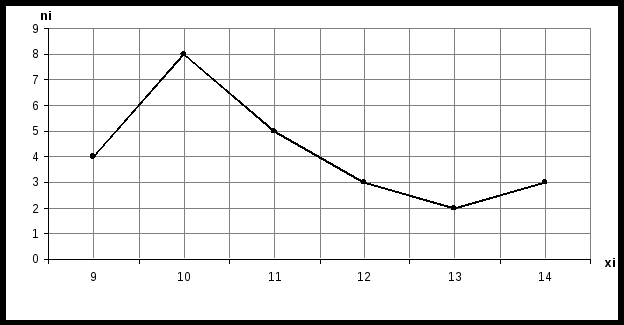   Рис. 1. Полигон частот 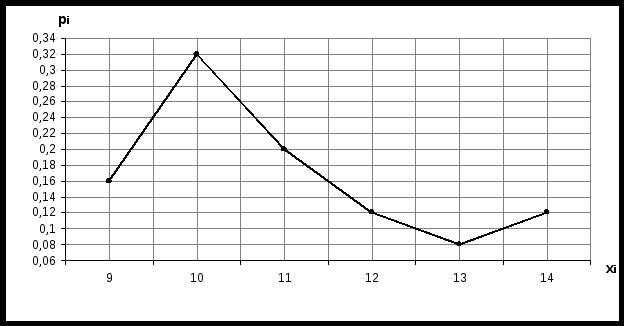   Рис. 2. Полигон относительных частот Рис. 1. Полигон частот 4) Построим эмпирическую функцию распределения F*(х): Эмпирическая функция распределения определяется следующим образом: 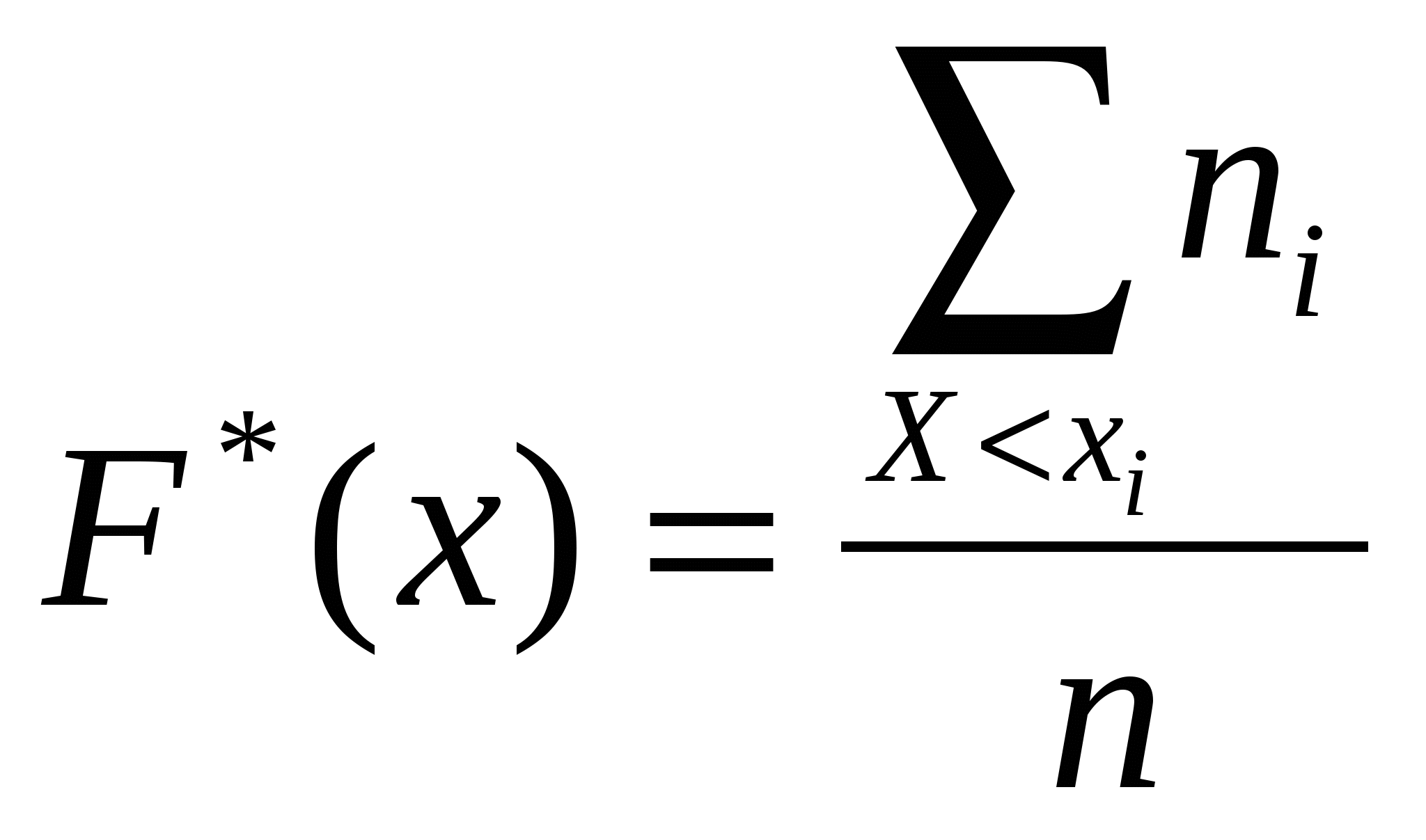 . .Разобьем числовую прямую на интервалы: (-;9]; (9;10]; (10;11]; (11;12]; (12;13]; (13;14]; (14; +). Найдем значения функции - при х 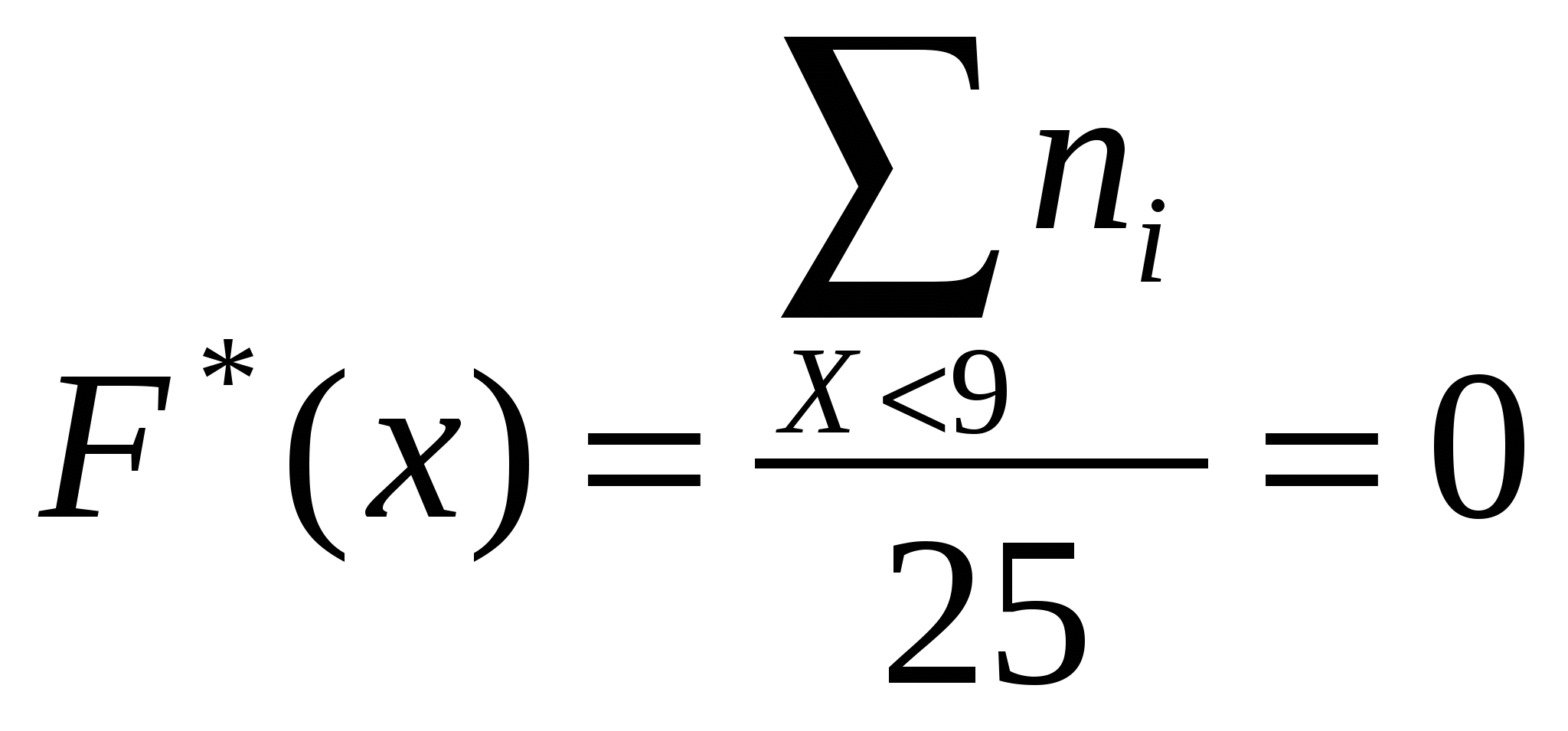 , т.к. в этом промежутке случайная величина Х не принимает ни одного значения, меньшего х=9. , т.к. в этом промежутке случайная величина Х не принимает ни одного значения, меньшего х=9.- при х 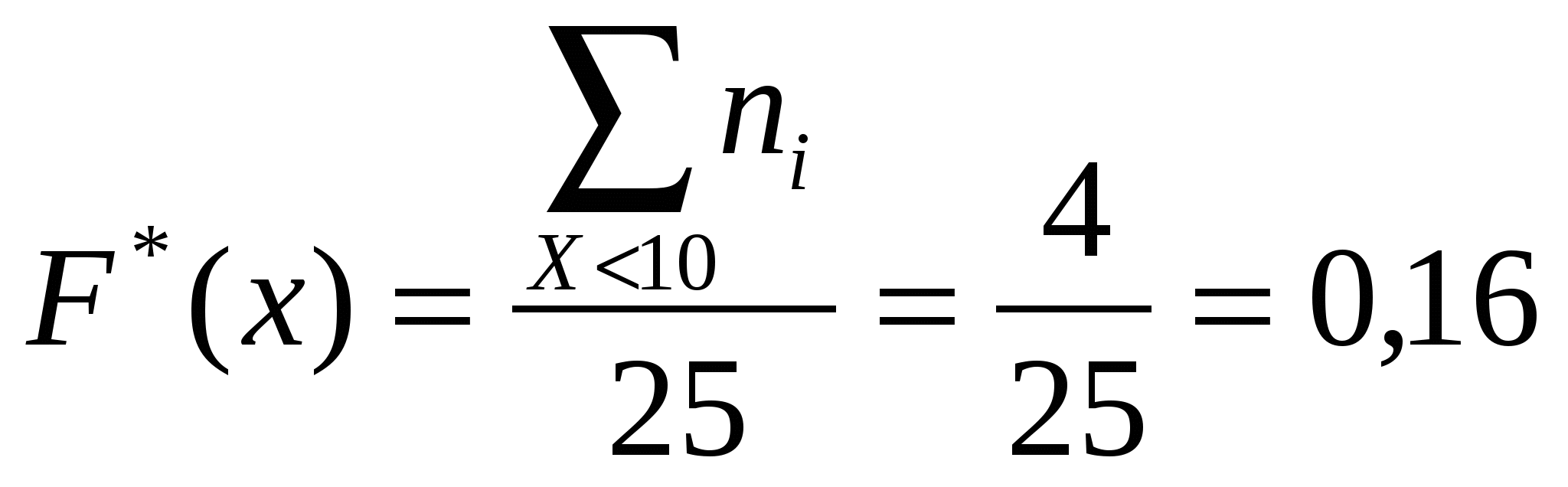 , т.к. в этом промежутке случайная величина Х принимает четыре раза значение х1=9, меньшее х=10. , т.к. в этом промежутке случайная величина Х принимает четыре раза значение х1=9, меньшее х=10.- при х 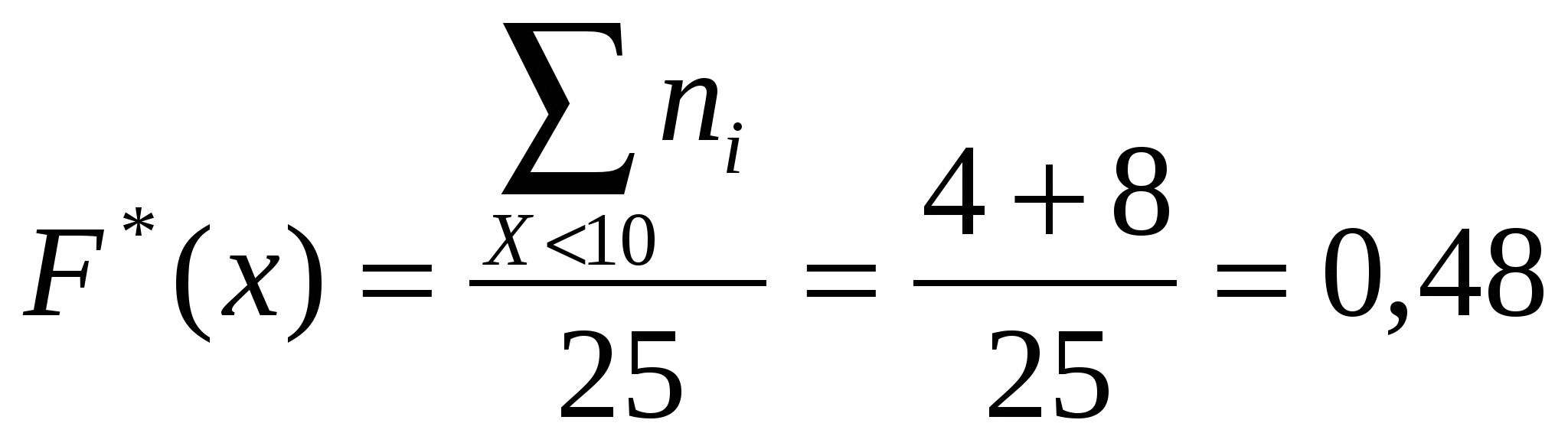 , т.к. на данном промежутке Х принимает значение х1=9 четыре раза и х2=10 восемь раз, меньшие х=11. , т.к. на данном промежутке Х принимает значение х1=9 четыре раза и х2=10 восемь раз, меньшие х=11.И т.д. Следовательно, интегральная функция распределения будет иметь вид: 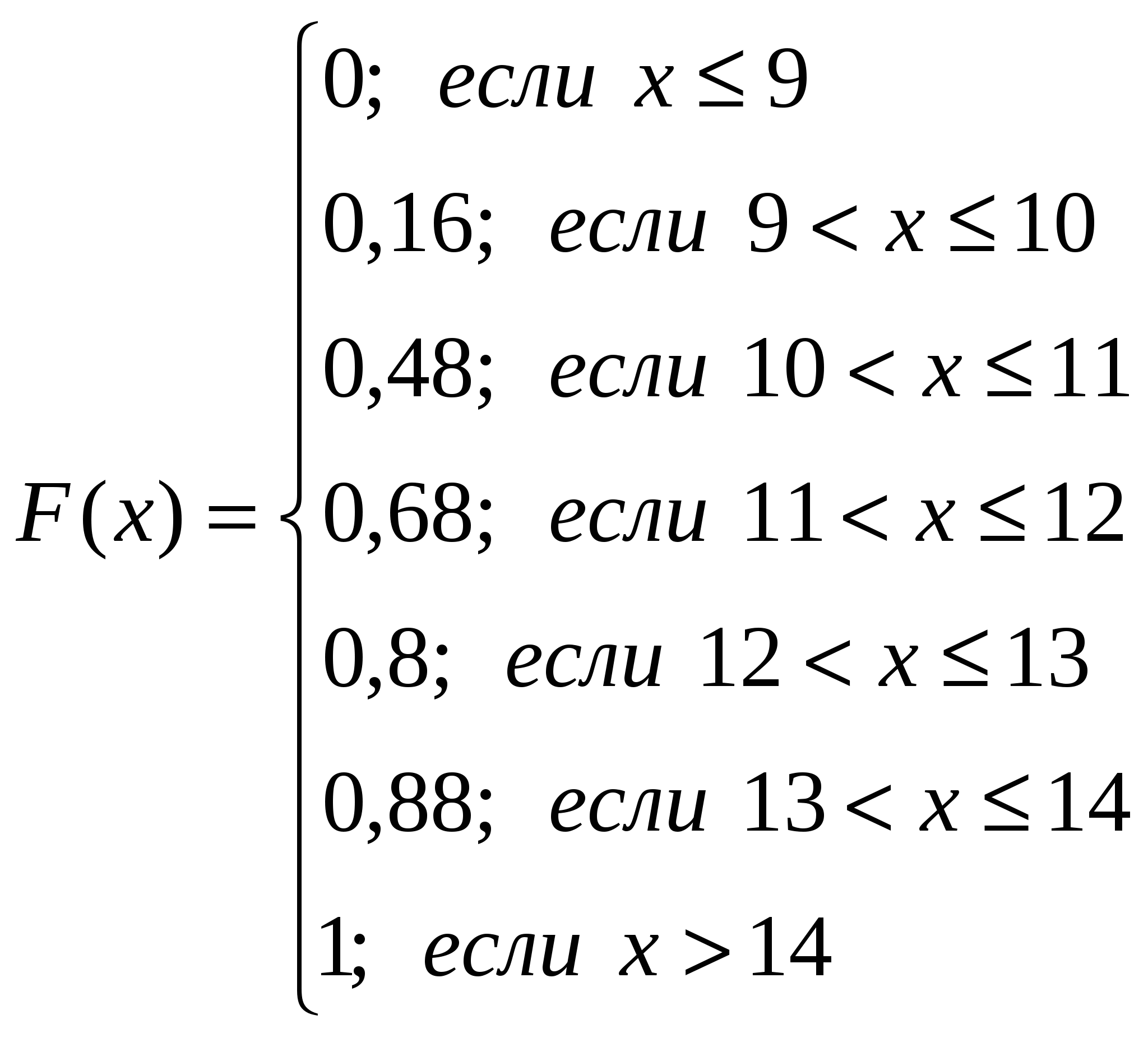 Построим кумуляту: 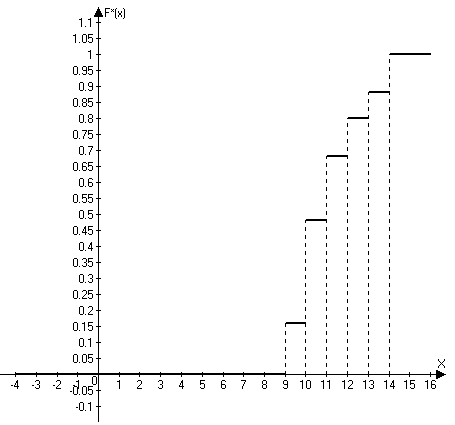 Рис.3. Кумулята 5) Мода M0 - это вариант, имеющий наибольшую частоту. В данном распределении М0=10. Медиана - это вариант, находящийся в середине вариационного ряда. В дискретном ряду данных, содержащем нечетное количество наблюдений, медиана находится по формуле: 6) Вычислим числовые характеристики: - выборочное среднее: - выборочная дисперсия: 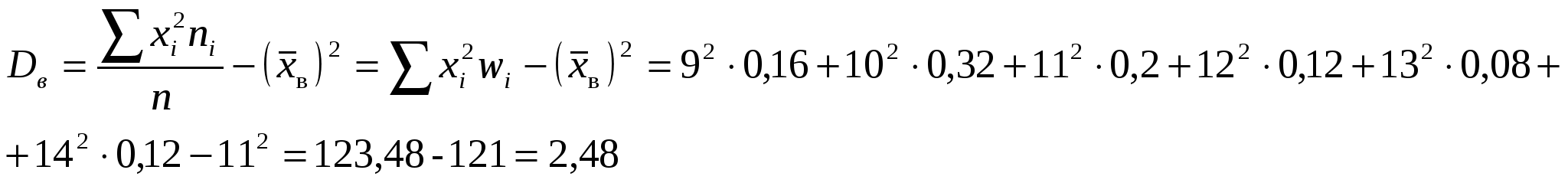 -среднее квадратическое отклонение (СКО): - «исправленная» дисперсия (несмещенная оценка дисперсии): - «исправленная» СКО (несмещенная оценка СКО): 7) Коэффициент вариации: Так как коэффициент вариации менее 33%, то совокупность данных полученной выборки - однородна. 8) Оценим с надежностью γ = 0,95 и γ = 0,99 математическое ожидание, дисперсию и СКО нормально распределенною признака генеральной совокупности с помощью доверительных интервалов. а) Доверительный интервал для математического ожидания а при неизвестной генеральной дисперсии где Для Для б) Доверительный интервал для неизвестной дисперсии 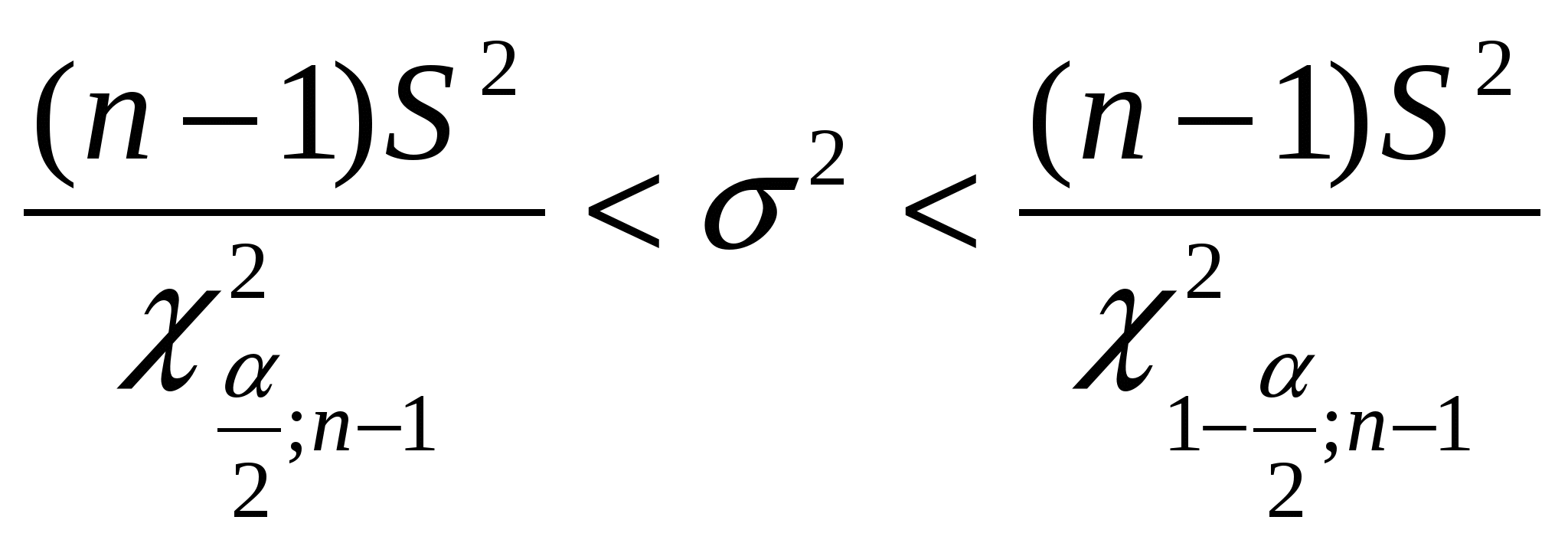 , ,где Для Для б) Доверительный интервал для неизвестного СКО 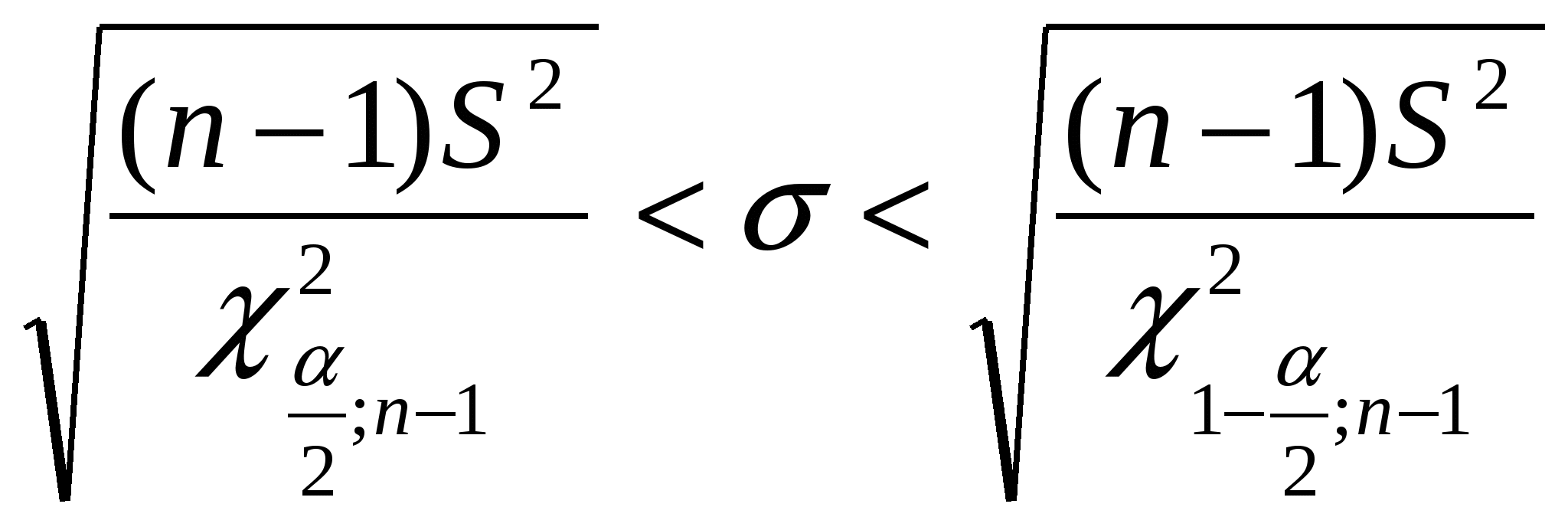 . .Для Для Ответ: с надежностью 95% с надежностью 99% Задание 2. Выборка годовых объемов привлеченных депозитов 100 коммерческих банков представлена в таблице (усл. ед.): Требуется: а) представить объем привлеченных депозитов в виде вариационною ряда, найти моду и медиану выборки: б) найти размах варьирования ряда и разбить его на 9 интервалов; в) построить гистограмму частот и относительных частот, с помощью гистограммы сделайте предварительный вывод о нормальном распределении генеральной совокупности; г) найти числовые характеристики выборки д) найти доверительные интервалы для математического ожидания и дисперсии для годовых объемов привлеченных депозитов при уровне значимости α=0,05 и α=0,01. Сравните эти оценки и запишите вывод; е) пользуясь критерием Пирсона, проверьте при уровне значимости
Решение: а) Представим объем привлеченных депозитов в виде вариационною ряда:
В данной выборке две моды: Медиана выборки, содержащей четное число данных находят по формуле: 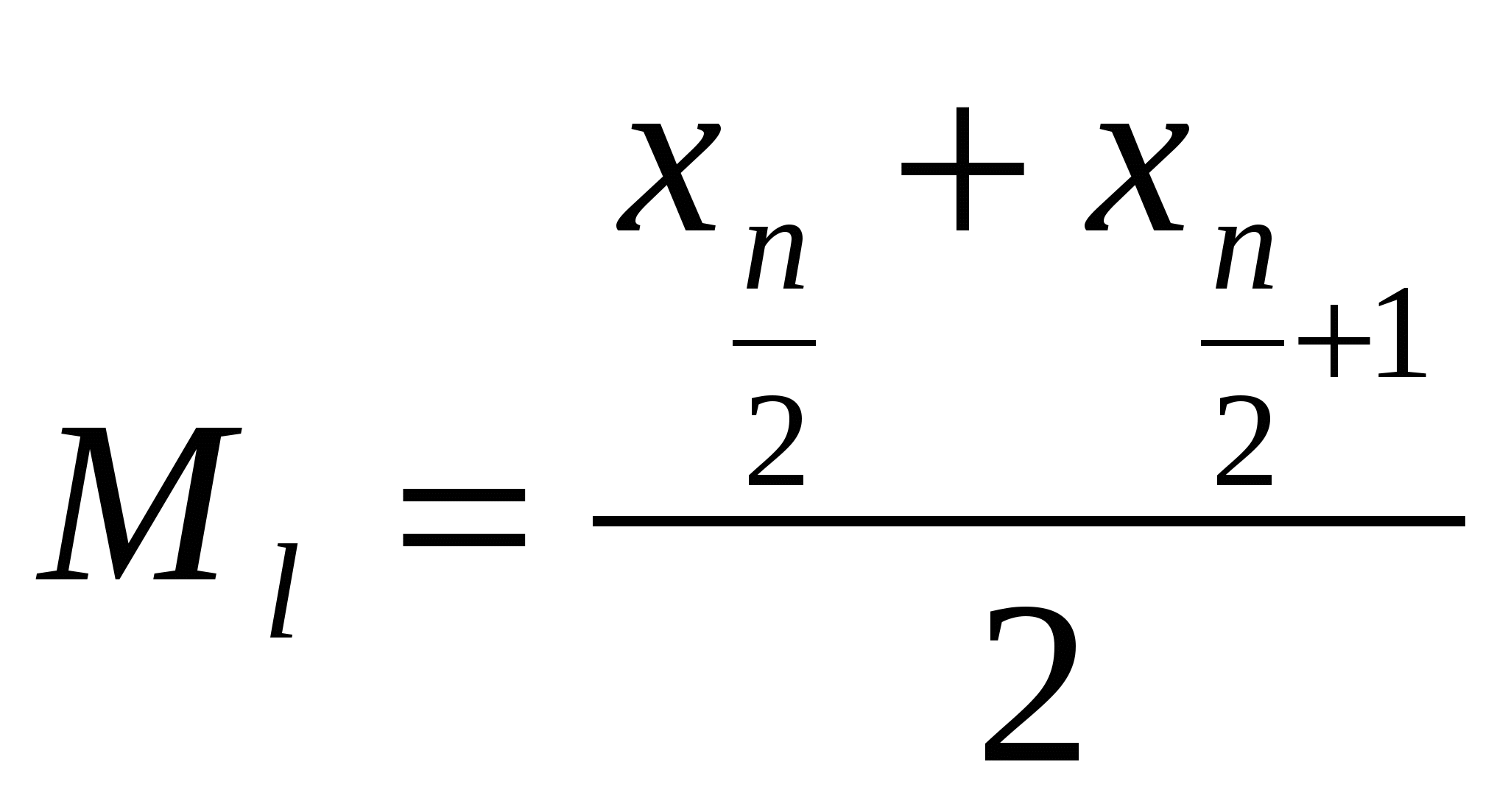 . .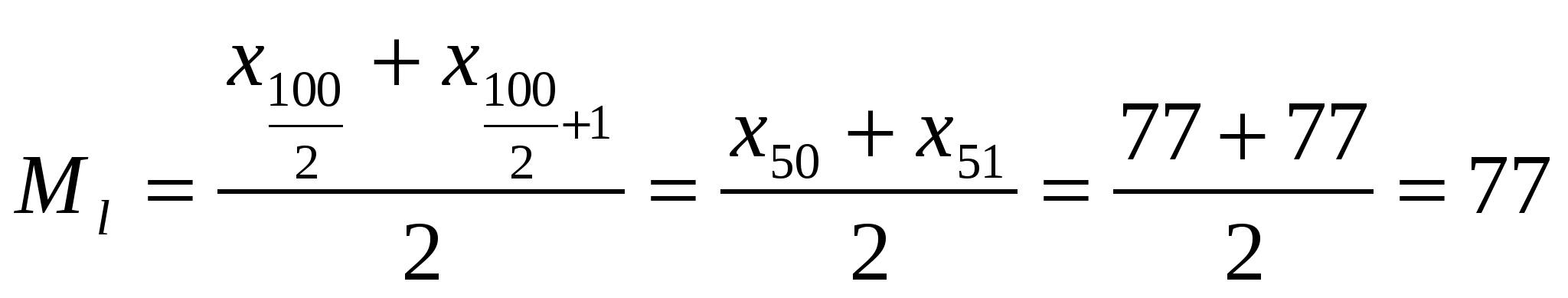 (усл.ед.) (усл.ед.)Т.е. у половины банков в данной выборке годовые объемы привлеченных депозитов не более 77 усл.ед., а половина - более 77усл.ед. б) Найдем размах варьирования ряда: k=9 - число интервалов разбиения Ширина интервала: Разбиения на интервалы производим по принципу полуоткрытого интервала: Рассчитаем дополнительно относительные частоты:
в) Построим гистограмму частот и относительных частот, с помощью гистограммы сделаем предварительный вывод о нормальном распределении генеральной совокупности. 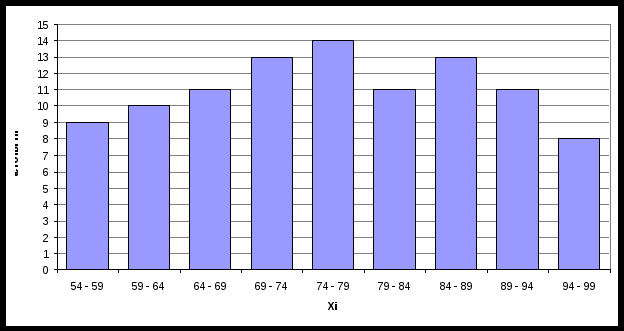 Рис.4. Гистограмма частот 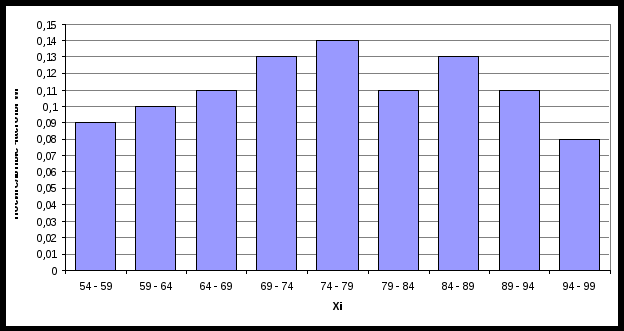 Рис.5. Гистограмма относительных частот 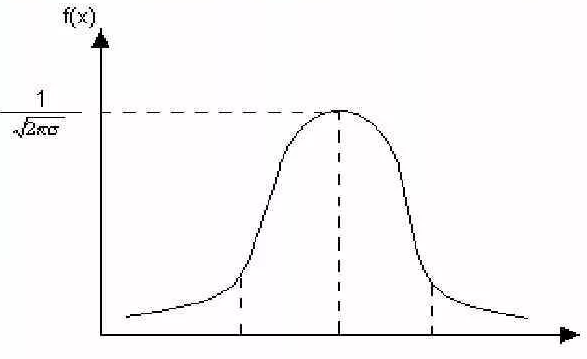 Рис.6. Плотность нормального распределения Сопоставляя график относительных частот с графиком плотности нормального распределения, видим, что эмпирическое распределение по форме существенно отличается от нормальной кривой, что говорит о том, то в ряд распределения данных подчиняется закону, отличному от нормального. г) На основе построенного интервального вариационного ряда найдем числовые характеристики выборки - выборочное среднее: где хi - середина интервала. Расчеты оформим в таблице.
- «Исправленная» выборочная дисперсия (несмещенная оценка дисперсии): - «Исправленное» выборочное среднее квадратическое отклонение (несмещенная оценка СКО): - Коэффициент вариации: Коэффициент вариации не превышает 33%, то говорит о качественной однородности банков по размеру годовых объемов привлеченных депозитов. д) Найдем доверительные интервалы для математического ожидания и дисперсии для годовых объемов привлеченных депозитов при уровне значимости α=0,05 и α=0,01. 1. Доверительный интервал для математического ожидания а при неизвестной генеральной дисперсии где Для Для 2. Доверительный интервал для неизвестной дисперсии 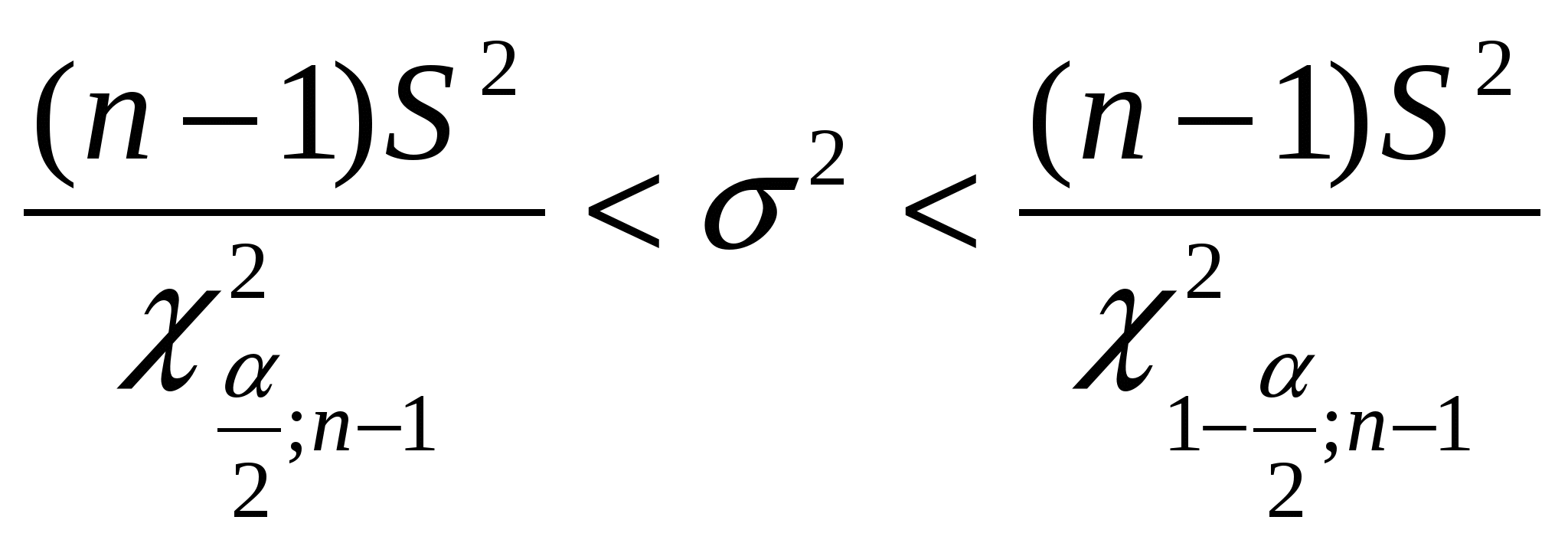 , ,где Для Для Вывод: с увеличением уровня значимости доверительный интервал сужается. е) Произведем оценку степени близости теоретического распределения (нормального) эмпирическому ряду с помощью критерия согласия Пирсона (уровень значимости Вычислим наблюдаемое значение критерия Пирсона: n=100 Полагаем левую границу 1-го интервала равной (-∞). Полагаем правую границу последнего интервала равной ∞. Оформим расчеты в таблице.
Для уровня значимости и числа степеней свободы k=s-3=9-3=6 (s- число интервалов распределения) находим критическое значение Так как Список литературы
|
