Контрольная работа № 3 по алгебре на тему _Уравнения и неравенст. Контрольная работа 3 по теме рациональные выражения. Уравнения Вариант 1 Решите уравнение а х

• Название: Контрольная работа 3 по теме рациональные выражения. Уравнения Вариант 1 Решите уравнение а х
• Дата: 13.04.2022
• Размер: 84.88 Kb.
• Имя файла: Контрольная работа № 3 по алгебре на тему _Уравнения и неравенст.docx
• Тип: Контрольная работа; #468307

Контрольная работа № 3

по теме «РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ. Уравнения»

В а р и а н т 1

1. Решите уравнение:

а) х³ – 64х = 0; б) = 2.

2. Решите биквадратное уравнение: 2х⁴ – 38х² + 96 = 0.

3. Решите неравенство:

а) 2х² – 13х + 6 < 0; б) 3х² – 27 > 0; в) 2х² – 3х + 7 > 0.

4. Решите неравенство, используя метод интервалов:

а) 2(х + 8) (3х – 12) > 0; б) 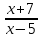< 0.

5. При каких значениях t уравнение 3х² + tх + 3 = 0 имеет два корня?

КОНТРОЛЬНАЯ РАБОТА № 3

ПО ТЕМЕ «РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ. УРАВНЕНИЯ»

В а р и а н т 2

1. Решите уравнение:

а) х³ – 121х = 0; б) = 1.

2. Решите биквадратное уравнение: у⁴ – 4у² – 45 = 0.

3. Решите неравенство:

а) 2у² – у – 15 > 0; б) 2х² – 32 < 0; в) х² + 6х + 20 < 0.

4. Решите неравенство, используя метод интервалов:

а) (х - 11) (х –9) < 0; б) 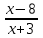> 0.

5. При каких значениях t уравнение 2х² + tх + 8 = 0 не имеет корней?

Контрольная работа № 3

по теме «РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ. Уравнения»

В а р и а н т 1

1. Решите уравнение:

а) х³ – 64х = 0; б) = 2.

2. Решите биквадратное уравнение: 2х⁴ – 38х² + 96 = 0.

3. Решите неравенство:

а) 2х² – 13х + 6 < 0; б) 3х² – 27 > 0; в) 2х² – 3х + 7 > 0.

4. Решите неравенство, используя метод интервалов:

а) 2(х + 8) (3х – 12) > 0; б) 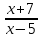< 0.

5. При каких значениях t уравнение 3х² + tх + 3 = 0 имеет два корня?


КОНТРОЛЬНАЯ РАБОТА № 3

ПО ТЕМЕ «РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ. УРАВНЕНИЯ»

В а р и а н т 2

1. Решите уравнение:

а) х³ – 121х = 0; б) = 1.

2. Решите биквадратное уравнение: у⁴ – 4у² – 45 = 0.

3. Решите неравенство:

а) 2у² – у – 15 > 0; б) 2х² – 32 < 0; в) х² + 6х + 20 < 0.

4. Решите неравенство, используя метод интервалов:

а) (х - 11) (х –9) < 0; б) 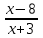> 0.

5. При каких значениях t уравнение 2х² + tх + 8 = 0 не имеет корней?

Решение вариантов контрольной работы № 3 ПО ТЕМЕ «РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ. УРАВНЕНИЯ»
В а р и а н т 1

1. а) х3 – 64х = 0;		б) = 2;
х (х2 – 64) = 0;		2(х2 – 1) – (3х – 1) = 2 · 4;
х = 0 или О т в е т: –8; 0; 8.	х2 – 64 = 0; х2 = 64; х = ±8.	2х2 – 2 – 3х + 1 – 8 = 0; 2х2 – 3х – 9 = 0; D = 9 + 72 = 81; х1 = = –1,5; х2 = = 3. О т в е т: –1,5; 3.

2. 2х⁴ – 38х² + 96 = 0.(можно сократить на 2)

Пусть х² = t, тогда получим:

2t² – 38t + 96 = 0;

D = 1444 – 768 = 676;

t₁ = , t₂ = 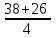= 16.

В е р н е м с я к з а м е н е:

х2 = 3; или х = ± .

х2 = 16; х = ±4.

О т в е т: –4; – ; ; 4.

3. а) 2х2 – 13х + 6 < 0; у = 2х2 – 13х + 6. Ветви параболы направлены вверх. 2х2 – 13х + 6 = 0; D = 169 – 48 = 121; х1 = , х2 = = 6.

О т в е т: .

б) 3х2 – 27 > 0; у = 3х2 – 27- график: парабола, т.к. а=3. Ветви параболы направлены вверх. 3х2 – 27 = 0; 3 х2 = 27; х = ±3.

О т в е т: (–∞; –3) (3; +∞).

в) 2х2 – 6х + 32 > 0; у =3х2 – 6х + 32. Ветви параболы направлены вверх. 2х2 – 3х + 7 = 0; D = 9 – 56 = –47 < 0. Парабола не пересекает ось х.

О т в е т: (–∞; +∞).

4. а) 2(х + 8) (3х – 12) > 0;	б) < 0;
х = –8; 4 – нули функции у = 2(х + 8) (3х – 12).	(х +7) (х - 5) < 0; х = –7; 5 – нули функции у = (х +7) ( х- 5).
О т в е т: (–∞;–8) (4; +∞).	О т в е т: (–7; 5).
5. 3х2 + tх + 3 = 0; D = t2 – 36. Уравнение имеет два корня, если D > 0, t2 – 36 > 0; t2 (–∞;–6) (6; +∞). О т в е т: (–∞;–6) (6; +∞).

В а р и а н т 2

1. а) х3 – 121х = 0;		б) = 1;
х (х2 – 121) = 0;		2(х2 + 6) – (8 – х) = 1 · 10;
х = 0 или О т в е т: –11; 0; 11.	х2 – 121 = 0; х2 = 121; х = ±11.	2х2 + 12 – 8 + х – 10 = 0; 2х2 + х – 6 = 0; D = 1 + 48 = 49; х1 = = –2; х2 = = 1,5. О т в е т: –2; 1,5.

2. у⁴ – 4у² – 45 = 0.

Пусть у² = t, тогда получим:

t² – 4t – 45 = 0;

t₁ = –5, t₂ = 9.

В е р н е м с я к з а м е н е:

у2 = –5 . или Нет решений.

у2 = 9; у = ±3.

О т в е т: ±3.

3. а) 2у2 – у– 15 > 0; g = 2у2 – у– 15 > 0. Ветви параболы направлены вверх. 2у2 – у – 15 = 0; D = 1 + 120 = 121; у1 = –2,5 у2 = = 3.

О т в е т: (–∞;–2,5) (3; +∞).

б) 2х2 – 32 < 0; у = 2х2 – 32. Ветви параболы направлены вверх. 2 х2 – 32 = 0; 2х2 = 32; х = ±4.

О т в е т: (–4; 4).

в) х2 + 12х + 80 < 0; у = х2 + 12х + 80 < 0. Ветви параболы направлены вверх. х2 + 6х + 20 = 0; D = 36 – 80 = –44 < 0. Парабола не пересекает ось х. О т в е т: нет решений.
4. а) (х - 11) (х –9) < 0;	б) > 0;
х = –11; 9 – нули функции у = (х -11) (х – 9).	б) (х - 8) (х +3) > 0; х = –3; 8 – нули функции у = (х -8) (х +3).
О т в е т: (9; 11).	О т в е т: (–∞;–3) (8; +∞).
5. х2 + tх + 16 = 0; D = t2 – 64. Уравнение не имеет корней, если D < 0, t2 – 64 < 0; t = ±8. О т в е т: (–8; 8).			t