Математика. Контрольная работа 3 семестр по дисциплине математика
 Скачать 36.27 Kb. Скачать 36.27 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» КОНТРОЛЬНАЯ РАБОТА 3 семестр ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА» 4 вариант Тула 2022 1. Определить тип и решить дифференциальное уравнение: 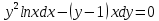 Это дифференциальное уравнение с разделяющимися переменными. 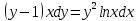 Разделяем переменные: 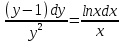 Интегрируем обе части: 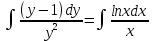 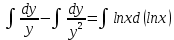 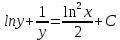 Общий интеграл дифференциального уравнения: 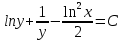 2. Определить тип и решить дифференциальное уравнение: 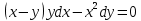 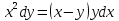 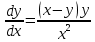 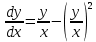 Это однородное дифференциальное уравнение первого порядка. Пусть 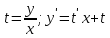 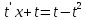 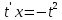 Получили уравнение с разделяющимися переменными: 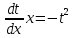 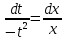 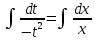 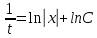 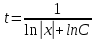 Общее решение дифференциального уравнения: 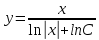 3. Определить тип и решить дифференциальное уравнение: 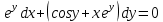 Это уравнение в полных дифференциалах 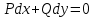 . .У нас: 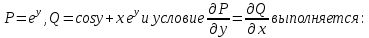 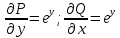 Общий интеграл ДУ: 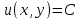 Функцию 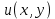 определяем из: определяем из: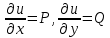 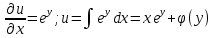 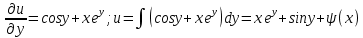 Отсюда: 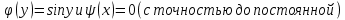 Общий интеграл ДУ: 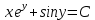 4. Найти решение задачи Коши: 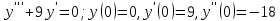 Задано линейное однородное дифференциальное уравнение 3-го порядка с постоянными коэффициентами. Характеристическое уравнение: 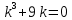 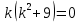 Характеристическое уравнение имеет один простой действительный корень 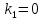 и два комплексно-сопряжённых корня и два комплексно-сопряжённых корня 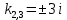 Им соответствуют три линейно независимых решения: 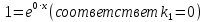 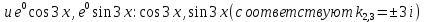 Общее решение заданного однородного уравнения – линейная комбинация этих решений: 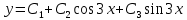 Тогда: 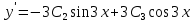 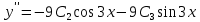 Из начальных условий: 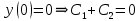 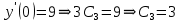 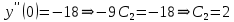 Из 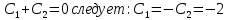 . .Искомое частное решение, удовлетворяющее заданным начальным условиям (решение задачи Коши): 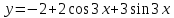 5. Найти общее решение уравнения: 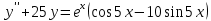 Задано линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Найдём сначала общее решение однородного ДУ: 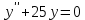 Характеристическое уравнение: 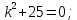 его корни 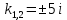 - комплексно-сопряжённые вида - комплексно-сопряжённые вида 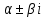 , общее решение в этом случае: , общее решение в этом случае: 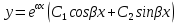 Значит (у нас 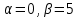 ): ): 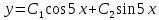 Общее решение исходного неоднородного уравнения – сумма общего решения однородного и частного решения исходного. Найдём частное решение исходного методом неопределённых коэффициентов. По виду правой части исходного ДУ 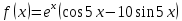 ищем его в виде (учитываем, что ищем его в виде (учитываем, что 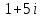 – не корень характеристического уравнения): – не корень характеристического уравнения):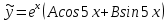 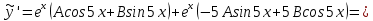 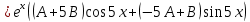 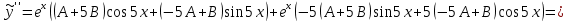 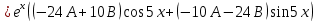 Подставляя в исходное ДУ, получим: 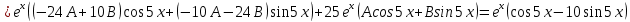 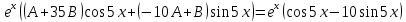 Отсюда: 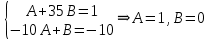 Получаем частное решение: 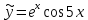 Общее решение исходного дифференциального уравнения: 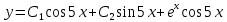 6. Исследовать на сходимость ряд 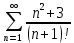 Это ряд с положительными членами, общий член ряда 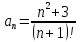 Применим признак сходимости Даламбера. Рассмотрим предел 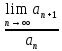 : :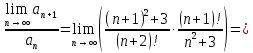 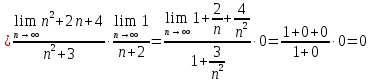 Так как этот предел существует и меньше единицы, то признаку Даламбера ряд сходится. 7. Исследовать на сходимость ряд 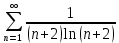 Это ряд с положительными членами. Общий член ряда 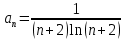 . .Докажем расходимость заданного ряда с помощью интегрального признака Коши: 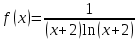 - неотрицательная невозрастающая функция при x>1 ; интеграл - неотрицательная невозрастающая функция при x>1 ; интеграл 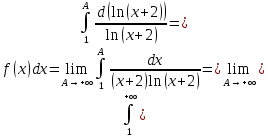 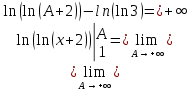 - расходится, значит расходится и ряд 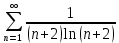 . .8. Исследовать на абсолютную и условную сходимость знакочередующийся ряд 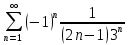 Докажем абсолютную сходимость заданного знакочередующегося ряда. Составим ряд из абсолютных величин членов исходного ряда: 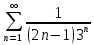 Для этого ряда с положительными членами применим признак сходимости Даламбера. Рассмотрим предел 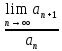 : :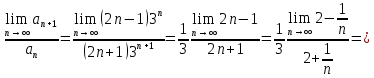 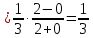 Так как этот предел существует и меньше единицы, то признаку Даламбера ряд сходится. Таким образом, заданный знакочередующийся ряд сходится абсолютно. 9. Найти область сходимости ряда 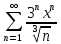 Радиус сходимости ряда: 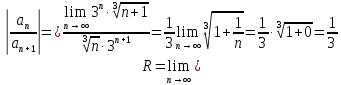 Интервал сходимости: 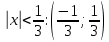 При 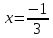 получаем знакопеременный ряд получаем знакопеременный ряд 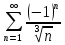 . Он сходится по признаку Лейбница: члены ряда монотонно убывают по абсолютной величине и стремятся к нулю: . Он сходится по признаку Лейбница: члены ряда монотонно убывают по абсолютной величине и стремятся к нулю: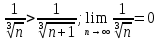 При 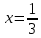 получаем ряд с положительными членами: получаем ряд с положительными членами: 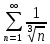 . Докажем расходимость этого ряда с помощью интегрального признака Коши: . Докажем расходимость этого ряда с помощью интегрального признака Коши: 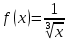 - неотрицательная невозрастающая функция при x>1 ; интеграл - неотрицательная невозрастающая функция при x>1 ; интеграл 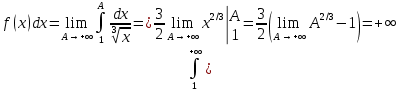 - расходится, значит расходится и ряд 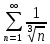 . . Таким образом, область сходимости ряда: 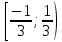 10. Разложить по степеням 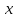 функцию функцию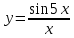 Разложение функции в ряд Маклорена: 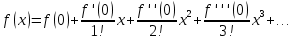 У нас 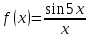 Разложим сначала функцию 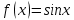 . .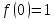 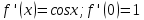 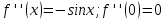 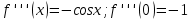 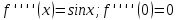 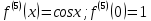 И так далее… Получаем разложение 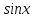 в ряд Маклорена: в ряд Маклорена: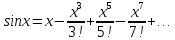 Берём 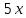 вместо вместо 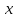 : :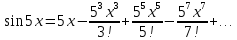 Поделив обе части на 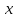 , получаем искомое разложение заданной функции: , получаем искомое разложение заданной функции: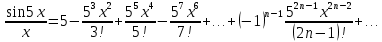 11. Брошены две монеты, причем на первой выпала решка. Найти вероятность того, что на монетах выпало две решки. Обозначим события: 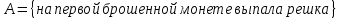 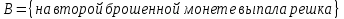 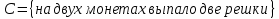 Вероятности событий 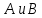 : :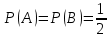 Событие 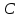 – произведение событий – произведение событий 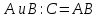 . Поскольку события . Поскольку события 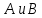 независимые, то по теореме умножения вероятностей: независимые, то по теореме умножения вероятностей: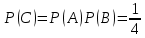 В задаче фактически требуется определить условную вероятность события 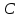 при условии выполнения события при условии выполнения события 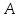 . По теореме умножения вероятностей: . По теореме умножения вероятностей: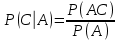 Поскольку событие 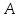 входит в событие входит в событие 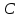 , то , то 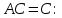 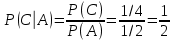 12. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из трех проверенных изделий хотя бы одно нестандартное. Обозначим: 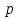 – вероятность события “проверяемое изделие стандартно”, по условию – вероятность события “проверяемое изделие стандартно”, по условию 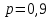 . Поскольку события “проверяемое изделие стандартно” независимы при трёх испытаниях (трёх проверках), то вероятность того, что событие произойдёт все три раза при трёх испытаниях по теореме умножения вероятностей равна . Поскольку события “проверяемое изделие стандартно” независимы при трёх испытаниях (трёх проверках), то вероятность того, что событие произойдёт все три раза при трёх испытаниях по теореме умножения вероятностей равна 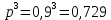 . .Найти вероятность того, что из трех проверенных изделий хотя бы одно нестандартное, как вероятность противоположного события (по отношению к событию “все три изделия стандартны”), равна: 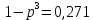 13. В партии из 12 деталей находятся 5 бракованных. Вынимают из партии наудачу 4 детали. Определить, какова вероятность того, что все окажутся бракованными. 4 детали из 12 можно выбрать 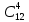 способами – число сочетаний из 12 элементов по 4: способами – число сочетаний из 12 элементов по 4: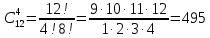 Это есть число всех элементарных исходов в результате опыта – выбор 4 деталей из 12: 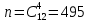 . Подсчитаем число благоприятных исходов . Подсчитаем число благоприятных исходов 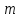 для появления события “все выбранные 4 детали окажутся бракованными”. Это число равно для появления события “все выбранные 4 детали окажутся бракованными”. Это число равно 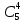 – числу сочетаний из 5 элементов (число всех бракованных деталей) по 4: – числу сочетаний из 5 элементов (число всех бракованных деталей) по 4: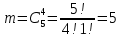 Поделив это число на общее число элементарных исходов, получим искомую вероятность того, что все выбранные детали окажутся бракованными: 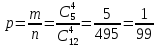 14. В спартакиаде участвуют: из первой группы 11 студентов, из второй – 14. Студент первой группы попадает в сборную университета с вероятностью 0,9, для студента второй группы эта вероятность равна 0,7. Найти вероятность того, что выбранный наудачу студент попадет в сборную университета. Обозначим события: A = {выбранный студент попадёт в сборную университета} 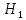 = {выбран студент первой группы} = {выбран студент первой группы}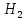 = {выбран студент второй группы} = {выбран студент второй группы}По условию задачи вероятности гипотез 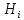 равны (учитываем, что всего в спартакиаде участвуют 11+14 = 25 студентов): равны (учитываем, что всего в спартакиаде участвуют 11+14 = 25 студентов): 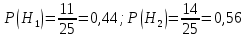 Условные вероятности события A (при условии выполнения 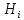 ) по условию задачи: ) по условию задачи: 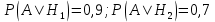 Вероятность того, что выбранный наудачу студент попадет в сборную университета, вычисляется по формуле полной вероятности: 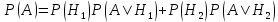 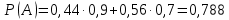 15. Дано следующее распределение дискретной случайной величины Х:
Известно, что математическое ожидание 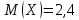 . Найти . Найти 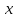 . .Сначала находим значение 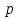 , исходя из того, что в сумме все вероятности дают единицу: , исходя из того, что в сумме все вероятности дают единицу: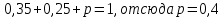 Математическое ожидание дискретной случайной величины X вычисляется по формуле: 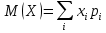 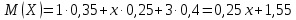 По условию, 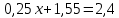 Отсюда: 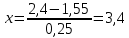 |
