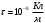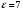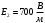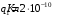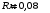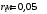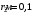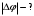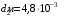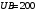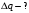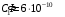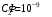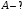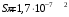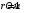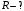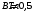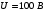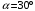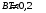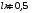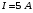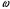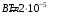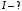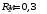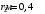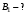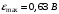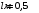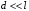Физика. 5 - Физика 3,4. Контрольная работа 3 Вариант Расчётнографическое задание iii
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
|
Физика. Контрольная работа 3,4. Вариант 5. Расчётно-графическое задание III 1.18. По тонкой нити, изогнутой по дуге окружности, равномерно распределён заряд с линейной плотностью 10 нКл/м. Определить напряжённость электрического поля, создаваемого таким распределением зарядов в точке, совпадающей с центром кривизны дуги. Радиус окружности дуги 5 см. Дуга составляет 1/3 полуокружности.
 Выберем оси координат так, чтобы начало координат совпало с центром кривизны дуги, а ось 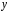 была симметрична расположена относительно концов дуги. была симметрична расположена относительно концов дуги. Выделим элемент длины  с зарядом с зарядом 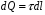 , который можно считать точечным. , который можно считать точечным. Найдем напряженность  , создаваемую зарядом , создаваемую зарядом  : :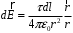 , где , где  - радиус-вектор, направленный от элемента - радиус-вектор, направленный от элемента  к точке, напряженность в которой вычисляется, к точке, напряженность в которой вычисляется,  - электрическая постоянная. - электрическая постоянная.Выразим вектор  через проекции через проекции  и и  . . , где , где 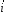 и и 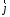 - единичные векторы. - единичные векторы. В силу симметрии интеграл 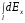 равен нулю. равен нулю.Тогда,  , где , где 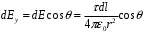 . .Так как  и и  , то , то 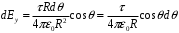 . .Приняв во внимание, что дуга расположена симметрично относительно оси 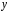 , берем пределы интегрирования от , берем пределы интегрирования от 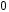 до до  и удваиваем результат: и удваиваем результат: . .Получаем, 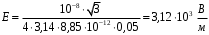 . .Ответ. 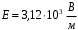 . .1.36. Плоскопараллельная диэлектрическая пластинка ( = 7) толщиной 4 мм равномерно заряжена по объёму. Напряжённость электрического поля вне пластины 700 В/м. Определить напряжённость электрического поля внутри пластинки на расстоянии 1 мм от её поверхности.
 Рассмотрим поле внутри пластины. Выберем в качестве замкнутой поверхности 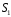 поверхность цилиндра высотой поверхность цилиндра высотой 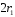 , который делится срединной плоскостью , который делится срединной плоскостью 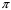 пополам. пополам.По теореме Гаусса 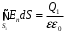 , где , где  - электрическая постоянная. - электрическая постоянная.Вектор 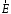 направлен от срединной плоскости направлен от срединной плоскости 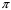 перпендикулярно пластине. Поэтому перпендикулярно пластине. Поэтому 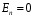 для всех точек боковой поверхности цилиндра и для всех точек боковой поверхности цилиндра и 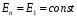 для всех точек обоих оснований. Тогда формула для всех точек обоих оснований. Тогда формула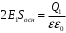 , где , где 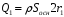 - заряд, расположенный внутри цилиндрической поверхности - заряд, расположенный внутри цилиндрической поверхности 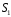 , , 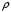 - объемная плотность заряда. - объемная плотность заряда.Тогда,  . .Так как 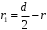 , то , то 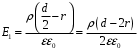 . Значит, . Значит,  . . Пусть  – поверхность цилиндра, высота которого больше толщины – поверхность цилиндра, высота которого больше толщины  пластины и который делится пополам срединной плоскостью пластины и который делится пополам срединной плоскостью 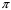 . . По теореме Гаусса  . .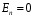 для точек боковой поверхности; для точек боковой поверхности;  для точек обоих оснований; для точек обоих оснований;  - заряд пластины, находящийся внутри поверхности - заряд пластины, находящийся внутри поверхности  . . Тогда, 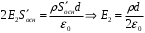 . Значит, . Значит, 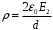 . .Тогда, 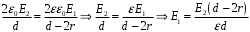 . .Получаем, 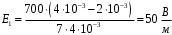 . .Ответ.  . .2.7. В вершинах равностороннего треугольника расположены положительные точечные заряды 210-10 Кл, 410-10 Кл и отрицательный заряд 210-10 Кл. Найти потенциал поля в центре треугольника, если сторона его 0,4 м.
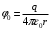 , где , где 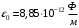 - электрическая постоянная. - электрическая постоянная.Значит, 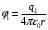 , , 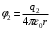 , , 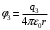 . .Расстояние от вершины треугольника до центра, можно найти как Радиус описанной окружности:  . .Тогда,  , ,  , , 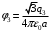 . .Суммарный потенциал равен алгебраической сумме:  . .Значит,  . .Получаем,  . .Ответ.  . .2.36. Шар из диэлектрика ( = 6) равномерно заряжен с объемной плотностью заряда 10-9 Кл/м3. Определить разность потенциалов между точками, лежащими на расстояниях 5 см и 10 см от центра, если радиус шара 8 см.
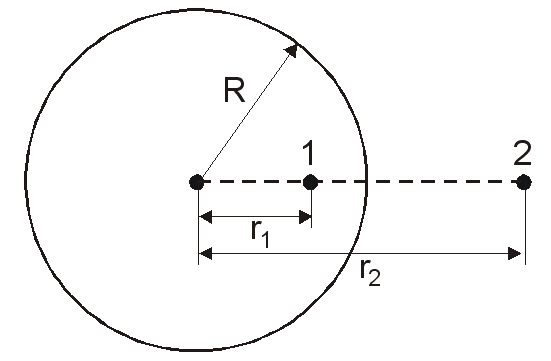 Связь 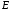 и и 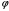 для центрально симметричного поля: для центрально симметричного поля: 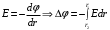 . .Напряженность электрического поля шара в зависимости от расстояния  до центра шара: до центра шара: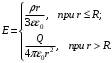 Заряд шара равен: 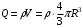 . .Значит,  Значит, 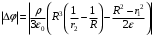 . .Получаем,  . .Ответ.  . .3.8. Расстояние между пластинами плоского воздушного конденсатора равно 3,2 мм, площадь пластин – 48 см2. Конденсатор подключен к батарее с ЭДС, равной 200 В. Найти изменение заряда конденсатора в результате раздвигания его пластин до расстояния 4,8 мм.
Значит, 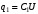 , , 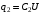 , где , где  , , 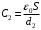 - емкости конденсаторов, - емкости конденсаторов, 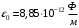 - электрическая постоянная. Значит, - электрическая постоянная. Значит,  , ,  . .Тогда, изменение заряда равно: 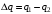 . .Значит, 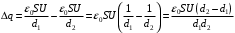 . .Получаем, 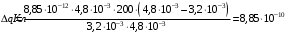 . .Ответ.  . .3.38. Два конденсатора, емкости которых 600 пФ и 1000 пФ, соединены последовательно. Батарею заряжают до напряжения 2000 В. Затем конденсаторы, не разряжая, соединяют параллельно. Определить работу разряда, происходящего при переключении.
 . .Значит, энергия в начальный момент времени равна:  . .Тогда, 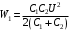 . .Также в начальный момент времени: 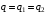 . Иначе говоря: . Иначе говоря: 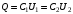 . .Значит,  . .Также можно записать для напряжения:  . .Значит,  . .При параллельном соединении напряжение на обоих конденсаторах выровняется: 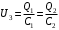 . Значит, . Значит,  . .По закону сохранения заряда имеем:  . .Значит,  . .Тогда, 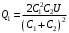 . Значит, . Значит, 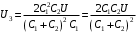 . .Энергия после их параллельного соединения равна:  . .Значит,  . .По закону сохранения энергии имеем: 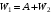 . Значит, . Значит,  . .Тогда,  . . Получаем, 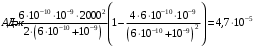 . .Ответ. 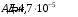 . .4.6. По медному проводу сечением 0,17 мм2 течет ток 0,15 А. Определить, какая сила действует на отдельные свободные электроны со стороны электрического поля. Удельное сопротивление меди 1.710-8 Омм.
 , где , где  - заряд электрона. - заряд электрона. Плотность тока равна: 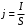 . .С другой стороны плотность тока равна:  . .Значит,  . Значит, . Значит, 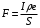 . . Получаем, 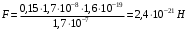 . .Ответ.  . .4.32. Какое сопротивление нужно подключить к пяти одинаковым последовательно соединенным источникам с ЭДС, равной 20 В, и внутренним сопротивлением 1 Ом каждый, чтобы потребляемая полезная мощность была максимальной?
 . .Мощность, выделяемая в сопротивлении равна:  . .Продифференцируем по  и приравняем к нулю: и приравняем к нулю:  . .Значит, максимальное сопротивление при  . . Получаем,  . .Ответ. 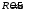 . .Расчётно-графическое задание IV 1.11. а) Определить чувствительность электронно-лучевой трубки осциллографа к напряжению, т.е. смещение пятна на экране, вызванное напряжением 1 В на управляющих пластинах. Длина пластин L, расстояние между ними d L, расстояние от конца пластин до экрана S > L. Разность потенциалов ускоряющего электрического поля равна U. б) Определить чувствительность электронно-лучевой трубки, если U = 10 кВ, l = 3 см, L = 30 см, d = 5 мм.
Если скорость электрона после предварительного ускорения v, то время пролёта отклоняющего конденсатора τ = L/v, а скорость в направлении отклонения u = U1eL/dmv, где U1 - отклоняющее напряжение, m - масса электрона. В таком случае смещение пятна δ = uS/v = U1eLS/dmv2, Поскольку mv2 = 2eU, то чувствительность γ = δ/U1 = LS/2dU. γ = 0,3*0,03/(2*0,005*104) = 0,9*10-4 (м/В). Ответ: γ = LS/2dU; γ = 0,9*10-4 м/В . 1.31. Вектор скорости однозарядного иона гелия, ускоренного в электрическом поле, направлен под углом 300 к силовым линиям однородного магнитного поля. Ускоряющая разность потенциалов равна 100 В, индукция магнитного поля 0,5 Тл. Вычислить силу, действующую со стороны магнитного поля на ион.
 , где , где  - заряд иона гелия, - заряд иона гелия,  - масса иона гелия. - масса иона гелия. По закону сохранения энергии имеем: 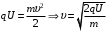 . .Значит,  . .Получаем,  . .Ответ.  . .2.6. На двух тонких невесомых проводниках в магнитном поле с индукцией 0,2 Тл горизонтально висит стержень длиной 0,5 м и массой 50 г. Силовые линии поля направлены вертикально вниз. На какой угол отклонятся проводники, удерживающие стержень, если по нему пропустить ток 5 А?
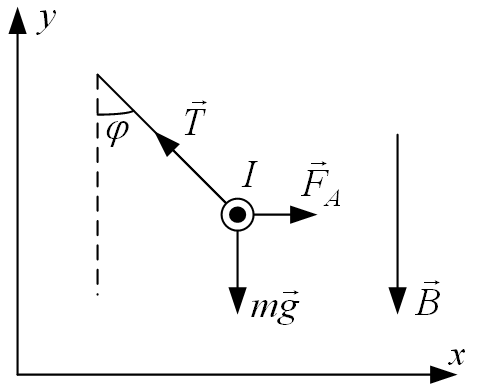 Условие равновесия проводника: 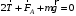 , где , где 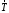 - натяжение проводника, - натяжение проводника, 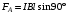 - сила Ампера, - сила Ампера,  - сила тяжести. - сила тяжести. В проекции на ось x имеем: 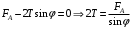 . .В проекции на ось y имеем:  . .Значит,  . Тогда, . Тогда, 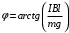 . . Получаем, 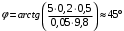 . .Ответ. 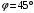 . .2.34. По поверхности диска равномерно распределен заряд с поверхностной плотностью σ. Определить отношение магнитного момента диска к моменту импульса. Радиус диска R, масса m, угловая скорость ω. Ось вращения проходит через центр диска и перпендикулярна его плоскости.
 На одной поверхности диска распределён заряд  , поэтому эквивалентный ток, создаваемый вращающимся диском определится как , поэтому эквивалентный ток, создаваемый вращающимся диском определится как 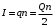 , где , где  - частота вращения диска. Тогда, - частота вращения диска. Тогда, 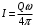 . .Магнитный момент эквивалентного тока, создаваемого вращающимся диском, несущим заряд, определится в этом случае как 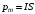 , где , где  - площадь поверхности диска. - площадь поверхности диска. Значит,  . . Заряд диска равен: 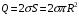 (так как заряд распределен по обеим поверхностям). (так как заряд распределен по обеим поверхностям). Тогда,  . .Но стороны у диска две, значит: 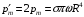 . .Момент импульса вращающегося диска равен произведению момента инерции диска на его угловую скорость:  . .Отношение магнитного момента диска к его моменту импульса равно: 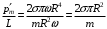 Ответ. 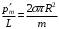 . .3.6. Контур с током имеет форму правильного шестиугольника со стороной 10 см. Определить силу тока в контуре, если индукция магнитного поля в центре контура равна 20 мкТл.
 Каждая сторона шестиугольника создает в центре магнитное поле с индукцией:  , где , где  - магнитная постоянная. - магнитная постоянная.Из рисунка находим, что  , а , а  . .Расстояние  равно: равно: 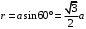 . .Тогда, 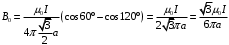 . .Значит, общая магнитная индукция равна:  . .Значит, 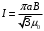 . .Получаем, 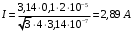 . .Ответ.  . .3.31. По двум коаксиальным тонкостенным трубам радиусами 10 см и 30 см текут токи соответственно 50 А и 100 А в противоположных направлениях. Найти индукцию магнитного поля в точках на расстояниях 20 см и 40 см от общей оси труб.
 По теореме о циркуляции имеем:  , где , где  - магнитная постоянная. - магнитная постоянная. С контуром 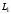 сцеплен только ток сцеплен только ток  цилиндра радиуса цилиндра радиуса  . Значит, . Значит, 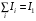 . .Тогда, 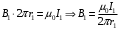 . .С контуром 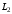 сцеплены токи сцеплены токи  и и  . .Токи текут в противоположных направлениях, значит, 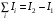 . .Тогда, 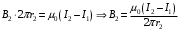 . .Получаем, 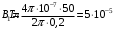 , ,  . .Ответ.  , , 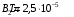 . .4.6. Круговой виток радиусом 0,2 м вращается в однородном магнитном поле с индукцией 0,1 Тл вокруг своего диаметра, составляющего угол 600 с направлением силовых линий магнитного поля. Определить частоту вращения витка, если максимальная ЭДС индукции составляет 0,63 В.
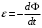 . .При вращении рамки магнитный поток, пронизывающий рамку, изменяется по закону:  , где , где  - площадь витка. Значит, - площадь витка. Значит,  . .Максимальное значение ЭДС при 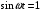 . Значит, . Значит, 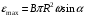 . .Угловая скорость равна: 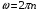 . Значит, . Значит, 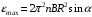 . .Тогда, 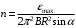 . .Получаем, 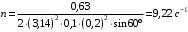 . .Ответ.  . .4.37. Определить длину тонкого провода, который надо ваять для изготовления соленоида длиной 0,5 м с индуктивностью 0,2 мГн. Диаметр сечения соленоида намного меньше его длины.
 , где , где  - площадь сечения соленоида, - площадь сечения соленоида,  - магнитная постоянная. - магнитная постоянная. Значит,  . .Длина проволоки равна:  . .Тогда,  . .Получаем,  . .Ответ. 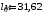 . . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||