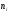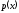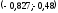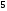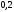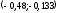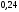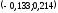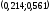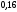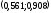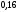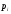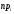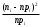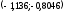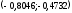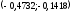Теория вероятностей и математической статистики Шульга Е.А.. Контрольная работа дисциплина Теория вероятности и математическая статистика Ф. И. О студента Шульга Екатерина Андреевна
 Скачать 374.38 Kb. Скачать 374.38 Kb.
|
 МИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Новосибирский государственный университет экономики и управления «НИНХ» (ФГБОУ ВО «НГУЭУ», НГУЭУ) Кафедра КОНТРОЛЬНАЯ РАБОТА Дисциплина: Теория вероятности и математическая статистика Ф.И.О студента Шульга Екатерина Андреевна Экономика предприятий и организаций Номер группы: ЭП91 Номер зачетной книжки: 183712 Номер варианта контрольной работы: 2 Проверил: __________________________________________ Новосибирск Содержание Задача № 1 3 Задача № 2 6 Задача № 3 8 Задача № 4 13 Список использованных источников 1 Задача № 1 3 Задача № 2 6 Задача № 3 8 Задача № 4 13 Список использованных источников 16 Задача № 1 Годовой облагаемый налогом доход Х наудачу выбранного частного предпринимателя города N является случайным с плотностью распределения 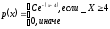 - Установить неизвестную постоянную С и построить график функции p(x) - Найти функцию распределения F(x) случайной величины и построить ее график - Вычислить математическое ожидание (среднее значение), дисперсию и среднее квадратическое (стандартное) отклонение рассматриваемой случайной величины - Во сколько раз число частных предпринимателей с доходом, облагаемым налогом меньше среднего, превышает число частных предпринимателей с доходом, облагаемым налогом больше среднего? Решение: Постоянная С 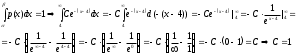 Тогда плотность распределения имеет вид 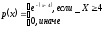 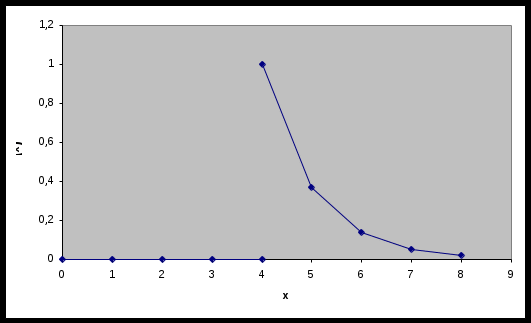 Рис. 1 Плотность распределения Функция распределения Т. к функция распределения изменяется от 0 до 1, она непрерывная и учитывая, что 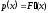 , то имеем , то имеем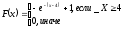 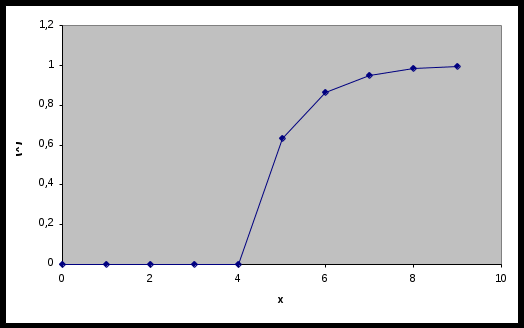 Рис. 2 Функция распределения Математическое ожидание (среднее значение) 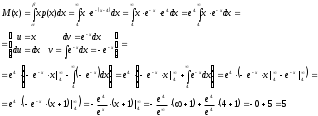 Дисперсия 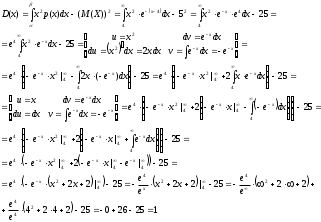 Среднее квадратическое отклонение 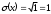 Вероятность того, что число частных предпринимателей с доходом, облагаемым налогом будет меньше среднего 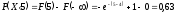 Вероятность того, что число частных предпринимателей с доходом, облагаемым налогом будет больше среднего 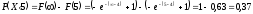 Т. о., число частных предпринимателей с доходом, облагаемым налогом меньше среднего превышает число частных предпринимателей с доходом, облагаемым налогом выше среднего в 0,63:0,37=1,7 раза Задача № 2 Производится три независимых выстрела по цели, причем вероятность попадания при каждом выстреле равна 0,6. Составить ряд и функцию распределения числа попаданий и представить их графически. Решение. 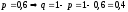 Случайная величина Х – число попаданий может изменяться от 0 до 3 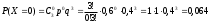 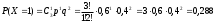 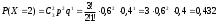 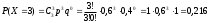 Получили ряд распределения Таблица 1. Ряд распределения
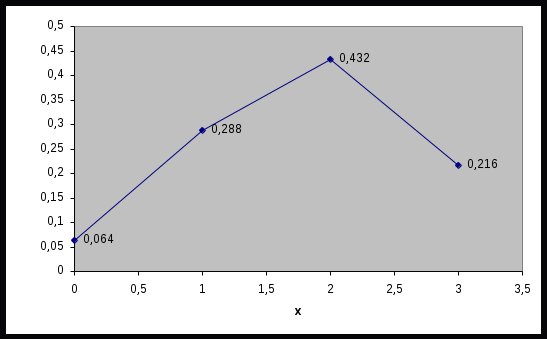 Рис. 1 Многоугольник распределения Функция распределения 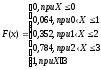 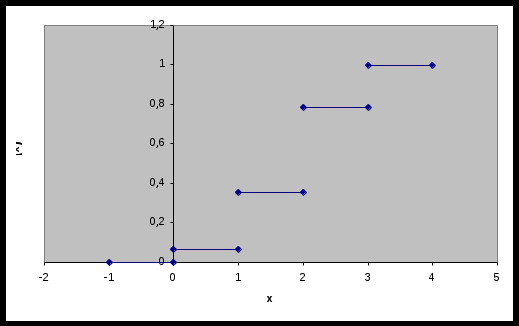 Рис. 2 Функция распределения Задача № 3 При проверке длины 25 деталей, изготовленных станком-автоматом, были обнаружены следующие отклонения от номинала: –0,307; 0,262; –0,372; 0,765; –0,140; –0,371; –0,113; –0,693; –0,550; –0,694; 0,545; 0,509; –0,150; –0,150; –0,559; –0,065; –0,112; 0,077; 0,698; –0,119; 0,861; 0,386; –0,827; 0,908; –0,047. Необходимо: Определить исследуемый признак и его тип (дискретный или непрерывный). В зависимости от типа признака построить полигон или гистограмму относительных частот. На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака. Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение. Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в п.3 закону распределения при уровне значимости 0,05. Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,95. С надежностью 0,95 проверить гипотезу о равенстве: а) генеральной средней значению 1; б) генеральной дисперсии значению 0,25. Решение: 1. Тип признака непрерывный, т.к. исходные цифры могут принимать любые дробные значения на определенном промежутке. Разобьем данные на 5 равных интервалов: Длина интервала 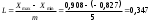
Гистограмма относительных частот 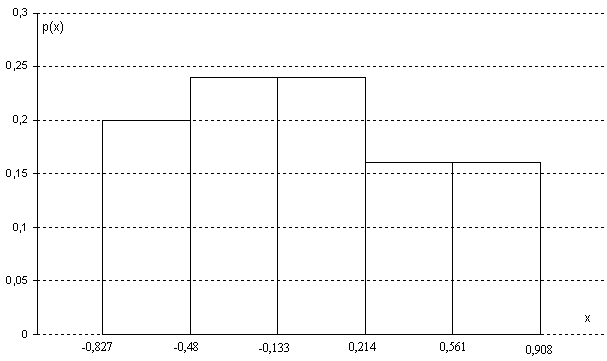 3. На основе анализа гистограммы распределения выдвигаем гипотезу о равномерное законе распределения исследуемого признака. 4. Среднее значение: 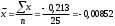 Дисперсия: 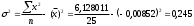 Среднее квадратическое (стандартное) отклонение: 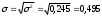 5. Вводим гипотезы: 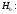 Исследуемый признак имеет равномерное распределение: Исследуемый признак имеет равномерное распределение: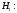 Исследуемый признак имеет другое распределение: Исследуемый признак имеет другое распределение:Условие принятия гипотезы 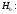 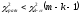 Вероятность попадания в интервалы: 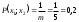
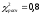 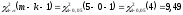 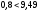 , следует гипотезу о равномерном распределении исследуемого признака принимаем. , следует гипотезу о равномерном распределении исследуемого признака принимаем.6. Доверительный интервал для генерального среднего, при доверительной вероятности 95%: 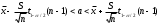 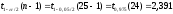 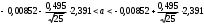 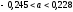 С вероятностью 95% генеральное среднее находится в интервале от 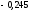 до до 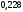 . .Доверительный интервал для генеральной дисперсии, при доверительной вероятности 95%: 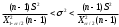 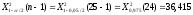 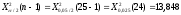 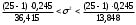 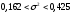 С вероятностью 95% генеральная дисперсия находится в интервале от 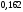 до до 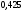 . .7а. Вводим гипотезы: 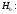 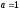 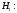 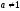 Условие принятия гипотезы 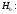 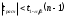 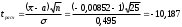 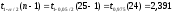 Условие принятия гипотезы выполняется 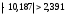 , следует с вероятностью 95% генеральное среднее нельзя считать равным 1. , следует с вероятностью 95% генеральное среднее нельзя считать равным 1.7б. Вводим гипотезы: 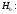 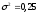 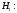 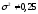 Условие принятия гипотезы 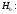 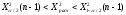 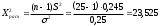 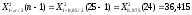 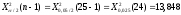 Условие принятия гипотезы выполняется 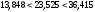 , следует с вероятностью 95% генеральную дисперсию можно считать равной 0,25. , следует с вероятностью 95% генеральную дисперсию можно считать равной 0,25.Задача № 4 В цехе с 10 станками ежедневно регистрировалось число вышедших из строя станков. Всего было проведено 200 наблюдений, результаты которых приведены ниже
Необходимо: Определить исследуемый признак и его тип (дискретный или непрерывный). В зависимости от типа признака построить полигон или гистограмму относительных частот. На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака. Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение. Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,99. При уровне значимости 0,05 проверить гипотезу о том, что число выбывших из строя станков имеет распределение Пуассона Решение: 1. Тип признака дискретный, т.к. исходные цифры могут принимать только целые значения.
Полигон относительных частот 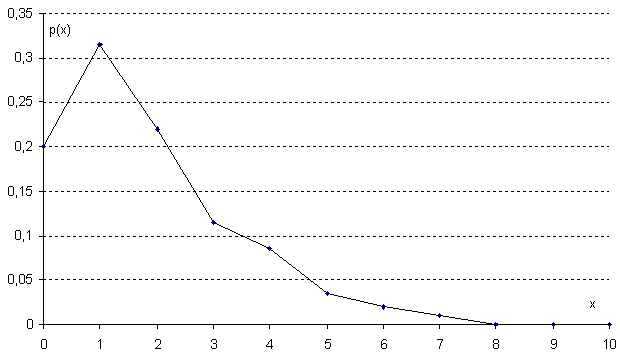 3. На основе анализа полигона относительных частот выдвигаем гипотезу о распределение Пуассона исследуемого признака. 4. Среднее значение: 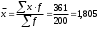 Дисперсия: 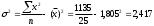 Среднее квадратическое (стандартное) отклонение: 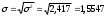 5. Доверительный интервал для генерального среднего, при доверительной вероятности 95%: 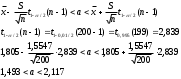 С вероятностью 99% генеральное среднее находится в интервале от 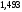 до до 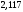 . .Доверительный интервал для генеральной дисперсии, при доверительной вероятности 99%: 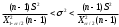 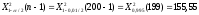 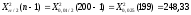 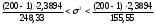 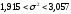 С вероятностью 99% генеральная дисперсия находится в интервале от 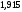 до до 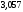 . .6. Вводим гипотезы: 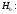 Исследуемый признак имеет распределение Пуассона: Исследуемый признак имеет распределение Пуассона: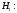 Исследуемый признак имеет другое распределение: Исследуемый признак имеет другое распределение:Условие принятия гипотезы 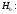 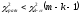 Вероятность попадания в интервалы: 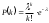 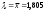
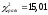 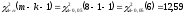 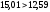 , следует гипотезу о распределении Пуассона исследуемого признака отвергаем. , следует гипотезу о распределении Пуассона исследуемого признака отвергаем.Список использованных источников Гмурман, В. Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В. Е. Гмурман.- 9-е изд.,стер. - М.: Высш. шк., 2013. – 478 с. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для вузов / В. Е. Гмурман. - 13-е изд., перераб. - М.: Высш. образование, 2019. - 404 с. |