Финансовые вычисления. Вариант 9. 9 вариант Расч.раб. Контрольная работа Финансовые вычисления
 Скачать 31.43 Kb. Скачать 31.43 Kb.
|
|
Министерство образования и науки РФ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Псковский государственный университет» Финансово-экономический факультет Кафедра экономики и финансов Расчётно-контрольная работа «Финансовые вычисления» Вариант 9 Студент: Соколова Т.А. Группа: 0073-05 Руководитель: Федорова Н.Ю. Псков 2014 Задача 1. На банковском вкладе проценты начисляются на основе сложной «плавающей» ставки, которая изменяется каждый год. Три года назад на счет положили 10000 руб., когда процентная ставка была 13%. В прошлом году она упала до 6%, а в этом году установлена на уровне 16%. Какая сумма будет на счете к концу текущего года? Дано: PV = 10000 руб. i1 = 13% i2 = 6% i3 = 16% n = 3 года Найти: FV Решение Для определения наращённой суммы в конце текущего года воспользуемся формулой определения будущей стоимости с переменной ставкой процента: FV = PV 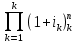 = PV* (1+ i1)n1(1+ i2)n2*…* = PV* (1+ i1)n1(1+ i2)n2*…*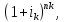 где гдеFV – наращённая (будущая) стоимость вклада; PV – первоначальная сумма вклада; i1, i2 … iK – ставка процента в каждом периоде; n1, n2…nk - продолжительность каждого периода в годах, тогда FV = 10000*(1+0,13)*(1+0,06)*(1+0,16) = 13894,48 руб. Ответ: По истечению 3-х лет сумма на счёте в банке составит 13894,48 руб. Задача 2. На депозитный счёт в банке сделан вклад в сумме 10000 руб. под 6 годовых на срок 16 лет. Какая часть дохода от вложения обеспечена применением сложного начисления процентов по сравнению с простым. Сумма вклада 10000 руб. Срок вклада 16 лет. Процентная ставка 6 % годовых. Какая часть дохода от вложения обеспечивается применением сложного начисления процентов по сравнению с простым. Решение FV = 10000*1.0616 = 25403,5 руб. I = FV – PV =25403,5 – 10000 = 15403,5 руб., следовательно, Доход от применения сложной процентной ставки по сравнению с простой = 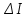 = Iслож – Iпрост = 15403,5 -9600 = 5803,5 руб. = Iслож – Iпрост = 15403,5 -9600 = 5803,5 руб.Часть дохода от вложения, обеспечивающая применением сложного начисления процентов по сравнению с простым = 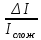 *100% = *100% =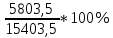 = 37,7% = 37,7% Задача 3. В банке получен кредит на сумму 10000 тыс. руб. для приобретения квартиры при условии погашения его равными ежегодными платежами. Срок погашения кредита составляет 16 лет, а процентная ставка равна 6% годовых. Необходимо рассчитать размер ежегодного платежа и составить график погашения кредита. Данные для расчёта представлены в задаче 1. График погашения кредита представляется в виде таблице. В банке взят кредит на сумму 10000 тыс. руб. с целью приобретения квартиры, при условии погашения его равными ежегодными платежами. Срок погашения кредита составляет 16 лет, а процентная ставка 6 % годовых. Рассчитать размер ежегодного платежа и составить график погашения кредита. Решение А = 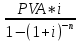 , ,A= 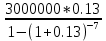 = 678332.41 руб. в год. = 678332.41 руб. в год.2. График погашения займов предоставлен в таблице 1 Таблица 1 График погашения займа
Задача 4. Вы выиграли приз в лотерее. Имеется два варианта получения приза. По первому вы получаете 55000 $ через год, а по второму 30000 $ сразу, и по 1000 $ в конце каждого года в течение последующих 30 лет. Какой вариант является более предпочтительным, если процентная ставка равна З %. В лотерею был выигран приз, который можно получить двумя способами: 1 способ: Получение приза в сумме 55000 долл. через год 2 способ: Получение 30000 долл. сразу и 1000 долл. в конце каждого года в последующие 30 лет. Какой способ предпочтительней (для того кто выиграл), если процентная ставка 3 % годовых. Решение: 1 случай PV = 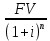 = = 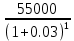 = 53398,06 долл. = 53398,06 долл.2 случай PVA = R 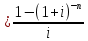 = 1000 = 1000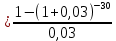 = 19600,33 долл. = 19600,33 долл.Учитывая, что 2-й случай предполагает первый платёж = 30000 долл., то PV = 49600,33 долл., следовательно 1 случай получения приза является более предпочтительным, т.к. сумма больше. Задача 5. Вы планируете приобрести квартиру через 3 года. Эксперты оценивают будущую стоимость недвижимости в размере 1 млн. рублей. По банковским депозитным счетам установлены ставки в размере 13% с ежеквартальным начислением процентов. Определить, какую сумму средств необходимо поместить на банковский депозитный счет, чтобы через 3 года получить необходимую для приобретения квартиры сумму. Решение PV = 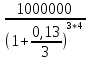 = 601091,58 руб = 601091,58 рубОтвет: Задача 6. Вы в возрасте 38 лет положили на счет 30000 долл. с тем, чтобы снять их со счета не раньше, чем вам исполнится 60 лет. Какая сумма будет у вас на счете, если процентная ставка составляет 13 %, а уровень инфляции – 9 %. Какова будет реальная стоимость ваших накоплений? Решение FVреал. = PV* ( 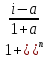 = 30000*(1+ = 30000*(1+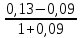 )22 = 66296,4 долл. )22 = 66296,4 долл.Задача 7. Вам осталось 38 лет до пенсии, и вы надеетесь прожить еще 15 лет после выхода на пенсию. Если вы начнете откладывать деньги начиная с текущего года, то каков будет размер ежегодных номинальных и реальных пенсионных выплат на каждый рубль ежегодных инвестиций при годовой процентной ставке 13 % и уровне инфляции 9 %. 9Решение: FVA= R* 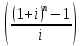 , где , гдеR = 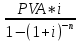 , где , где1 случай (если используется номинальная процентная ставка) FVA= R* 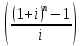 = 1* = 1*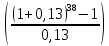 = 792,21 руб. = 792,21 руб.FVA = PVA = 792,21 руб. R = 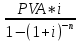 = = 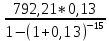 = = 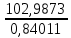 =122,59 руб. =122,59 руб.2 случай (если используется реальная процентная ставка) FVA= R* 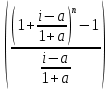 = 1* = 1*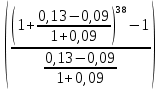 = = 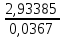 = 79,94 руб. = 79,94 руб.FVA = PVA = 79,94 руб. R = 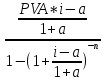 = = 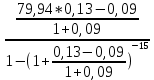 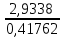 = 7,03 руб. = 7,03 руб.Задача 8. У вас есть возможность участвовать в инвестиционном проекте, который обеспечит поступление в конце первого года 25000 руб., в конце следующего – 20000 руб., а в конце третьего, последнего года вам требуется уплатить 48000 руб. Оцените целесообразность такого участия, если ставка дисконтирования составляет 9 %. Решение PV =  = 25000 = 25000 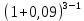 + 20000 + 20000 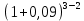 = 29702,5+21800=51502,5 руб. = 29702,5+21800=51502,5 руб.NPV = PV – IC = 51502,5 – 48000 = 3502,5 руб. Задача 9. Инвестор предполагает приобрести облигацию номиналом 10000 руб, по которой выплачивается 13 процентов годовых. Выплата процентов производится один раз в год. До погашения облигации остается 6 лет. Требуемая норма прибыли в течение первых трех лет – 20%, четвертый год – пятый год – 15%, 6 год и т.д. – 10 %. Определить курсовую цену облигации, а также доходность к погашению. Решение К.Ц. = 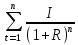 + + 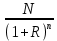 = = ( 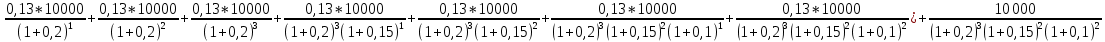 = 8565,13 руб. = 8565,13 руб.R = 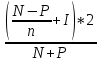 = = 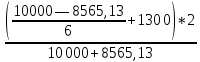 *100% = 16,58% *100% = 16,58%Задача 10. На фондовом рынке продаются акции акционерного общества «Альфа». Ожидаемые дивиденды в течение первых 3 лет составляют 70 руб. на акцию. В последующие годы прогнозируются темпы прироста дивидендов – 14 % в год. Требуемая норма прибыли на акцию – 19 % годовых. Определить цену акции, если инвестор собирается держать акцию неограниченно долго. Решение P = D* 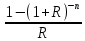 + + 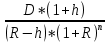 = 70* = 70*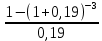 + +  = 70* = 70*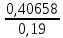 + + 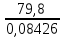 = 149,79+947,07 = 1096,86 руб. = 149,79+947,07 = 1096,86 руб. |
