Математика. Математика (2-е высшее, досдача). Контрольная работа Математика

• Название: Контрольная работа Математика
• Анкор: Математика
• Дата: 05.11.2022
• Размер: 230 Kb.
• Имя файла: Математика (2-е высшее, досдача).doc
• Тип: Контрольная работа; #771635

Контрольная работа «Математика» 2-е высшее (досдача)

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования
РОССИЙСКАЯ АКАДЕМИЯ НАРОДНОГО ХОЗЯЙСТВА и ГОСУДАРСТВЕННОЙ СЛУЖБЫ

при ПРЕЗИДЕНТЕ РОССИЙСКОЙ ФЕДЕРАЦИИ

СИБИРСКИЙ ИНСТИТУТ – ФИЛИАЛ РАНХиГС

ЦЕНТР ПЕРЕПОДГОТОВКИ СПЕЦИАЛИСТОВ

Математика
Письменное контрольное задание

для студентов дистанционного обучения
Тема: Роль государства в экономическом развитии общества

	Студент Куулар Эдуард Викторович
	Группа 11206
	Дата 5.11.2013г.
	Преподаватель

Новосибирск 2013г.

ИНСТРУКЦИЯ ПО ВЫПОЛНЕНИЮ

ПКЗ оформляется в Microsoft Word. Промежуточные выкладки можно опустить и не набирать, но обязательно дать обоснования полученных ответов. Например, в точке х=3 функция имеет разрыв первого рода, т.к. предел слева равен 4, а предел справа равен 10.

Выбор варианта осуществляется по приведенной ниже таблице. В первом столбце найдите свой номер в списке группы или в списке ЭЛЕКТРОННОЙ ВЕДОМОСТИ. Цифры в строке показывают номера задач из семи предложенных заданий, которые следует решить. Например, первый в списке решает 1-ю задачу из первого задания, 3-ю — из второго, 2-ю — из третьего и т. д.

Задания выполняются в том порядке, в котором они приведены ниже. Вам необходимо выполнить по возможности максимальное количество заданий. Максимальное количество баллов за все ПКЗ — 100 баллов.

Базовое пособие — УМК «Математика».

№ в списке	Номер задания
	1	2	3	4	5	6	7
1	5	3	2	1	9	10	1

1.Найти участки возрастания и убывания функций, классифицировать точки экстремума

5. Найти участки возрастания и убывания функций, классифицировать точки экстремума

Решение:

а. Найдем производную функции



б. при y возрастает

при y убывает

так как при переходе через точку производная меняет свой знак с плюса на минус, значит в точке - точка максимума функции y.

2. Найти определенные интегралы

3.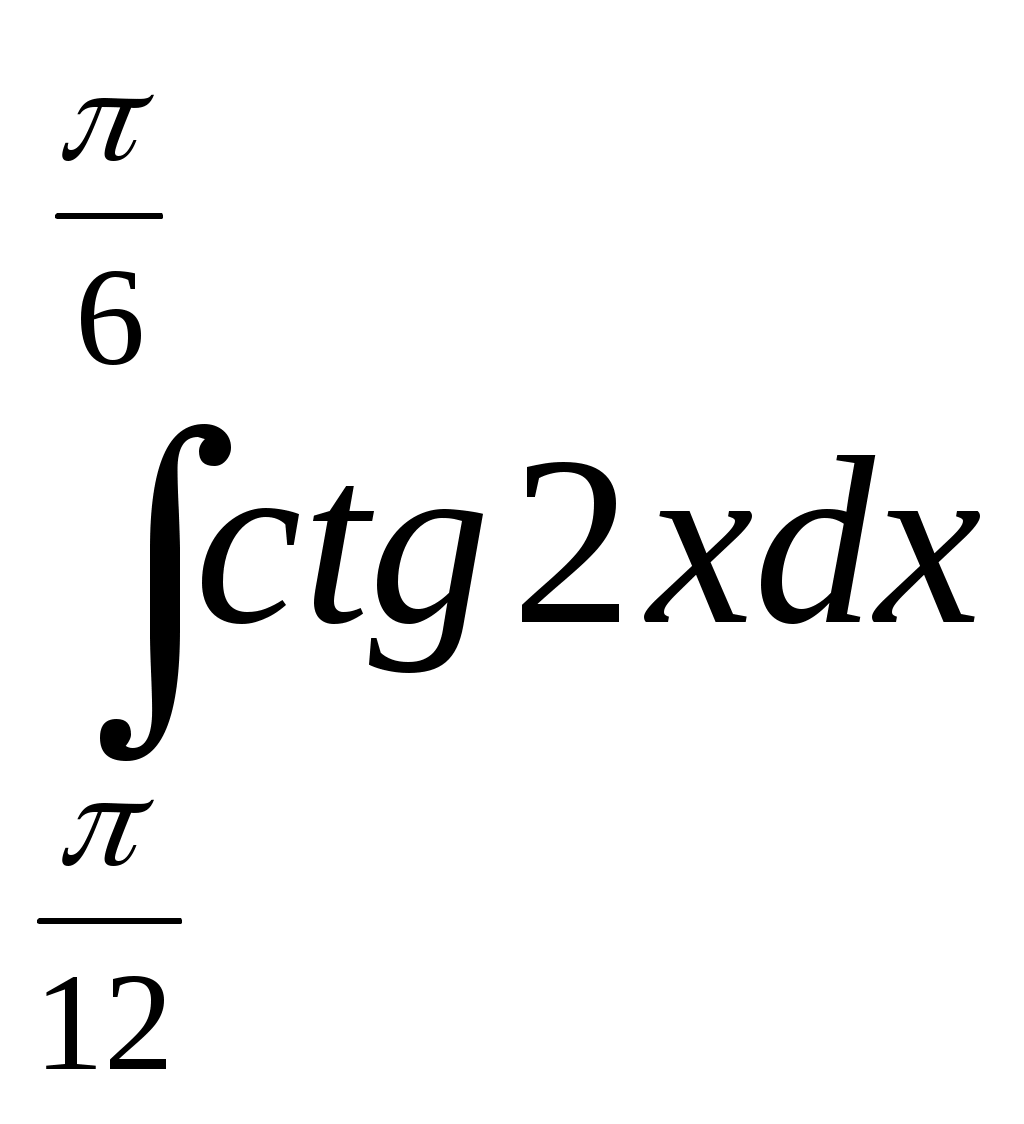

Решение:

Перепишем подынтегральное выражение:

ctg(2x)=cos(2x)/sin(2x)

Пусть u=sin(2x).

Тогда пусть du=2cos(2x)dx и подставим du/2:

∫1/2u*du

Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:

∫1/2udx=1/2∫1/u*dx

Интеграл 1/u есть ln(u).

Таким образом, результат будет: 1/2ln(u)

Заменим u:

1/2ln(sin(2x))

Следовательно:

1/2ln(sin(2*П/6)) - 1/2ln(sin(2*П/12))=0,275

3. Комбинаторика

2. Сколькими способами можно выбрать гласную и согласную буквы из слова КОНВЕРТ?

Решение:

Гласную можно выбрать двумя способами (О или Е), а согласную — пятью способами (К, Н, В, Р или Т).

2 · 5 = 10.

4.Теория вероятности (события)

1. Найти вероятность того, что четырехзначный номер случайно встреченного автомобиля состоит из одинаковых цифр.

Решение:

Решение. Каждая цифра номера может быть одной из десяти: 0, 1, 2, ..., 9. Испытанием является выбор какой-либо четверки цифр. Количество всех возможных номеров, т.е. число всех исходов, равно 10 • 10 • 10 • 10 = = 10 000. Пусть событие А состоит в том, что все цифры выбранного номера одинаковы. Благоприятных исходов будет 10: 0000, 1111, .... 9999. Итак, п = 10 000, т(А) = 10 и .
5. Формула Бернулли

9. Установлено, что виноградник поражен вредителями в среднем на 10%. Определить вероятность того, что из 5 проверенных кустов винограда будет поражен: а) один куст; б) не менее двух кустов.

Решение:

Запишем формулу Бернулли: - это вероятность того, что в n независимых испытаниях событие A произойдет k раз (0≤k≤n) при условии, что в каждом испытании вероятность события A остается одинаковой и равной p. В этой формуле n – число испытаний, q=1-p, - число сочетаний из n объектов по k. В данной задаче n=5, p=0.1, q=0.9.

а). Вероятность того, что из 5 проверенных кустов винограда будет поражен один куст, равна

.

б). Вероятность того, что из 5 проверенных кустов винограда будет поражено не менее двух кустов, равна



.

Ответ: Вероятность того, что из 5 проверенных кустов винограда будет поражен один куст, равна ; вероятность того, что из 5 проверенных кустов винограда будет поражено не менее двух кустов, равна .


6. Теория вероятности (случайные величины)

10. В ящике 12 белых и 18 черных шаров. Составить закон распределения количества белых шаров среди четырех, вынутых наугад. Построить многоугольник распределения. Найти математическое ожидание и дисперсию случайной величины.

Решение:

Вероятность белого =m/n=12/(12+18)=12/30=0,4; P=0,4(вероятность белого)

q=1-0,4=0,6

Найти закон распределения белых шаров среди вынутых 4-х шаров.

Возможные случаи:

1. 
   Ни одного белого (все черные)
   

x₀=→P(x=0/4)=C₄⁰*p⁰*q⁴=1*1*0,6⁴=0,1296

x₁=1→P(x=1/4)=C₄¹*p¹*q³=4*0,4*0,6³=1,6*0,216=0,3456

x₂=2→P(x=2/4)=C₄²*p²*q²=12/2*0,4²*0,6²=6*0,16*0,36=0,3456

x₃=3→P(x=3/4)=C₄³*p³*q=4*0,064*0,6=0,1536

P(x=4/4)=C₄⁴*p⁴*q⁰=0,064*0,4=0,0256;

Итак P(x=0/4)=0,1296; P(x=1/4)=0,3456

P(x=2/4)=0,3456; P(x=3/4)=0,1536; P(x=4/4)=0,0256

Проверка ∑P=1→0,1296+0,3456+0,3456+0,1536+0,0256=1

Следовательно закон распределения белых шаров среди вынутых 4-х шаров будет:

X	0	1	2	3	4
P	0,1296	0,3456	0,3456	0,1536	0,0256

2. 
   Построить многоугольник распределения:
   

М₁(x_1;p₁)=M(0;0,13); M₂(1;0,35) М₃(2;0,35) M₄(3;0,15); М₅(4;0,02)
Многоугольник распределения: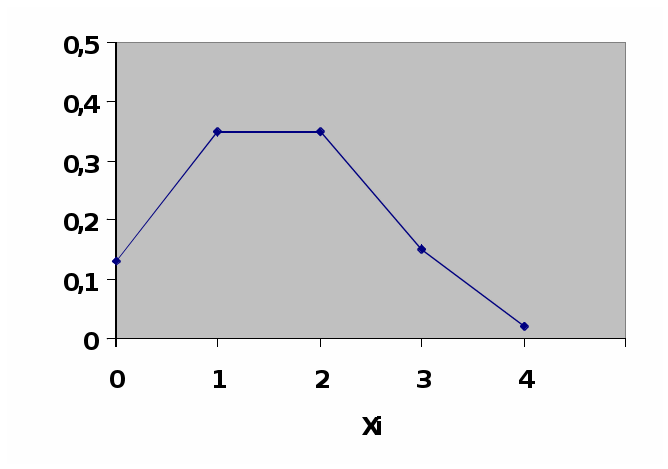

3. 
   Найдем математическое ожидание M(x)
   

M(x)=∑x_i*p_i = 0*0,13+1*0,35+2*0,35+3*0,15+4*0,02=1,5

M(x)=0+0,35+0,7+0,45+0,08=1,58
Найдем дисперсию D(x)

4

D(x)=∑=(x_i-M(x))²*p_i

i=0

D(x)=(0-1,5)²*0,13+(1-1,5)²*0,35+(2-1,5)²*0,35+(3-1,5)²*0,15+(4-1,5)²*0,02=0,93

Среднее квадратическое отклонение

Ϭ=√D(x)=√0,93=0,96

Ответ: дисперсия равна 0,93; среднее квадратическое отклонение равно 0,96

7. Математическая статистика

1. Проверяющий в течение контрольного периода записывал время ожидания нужного автобуса (в минутах) и получил следующие данные:

1,21	4,71	4,45	0,27	7,42	8,45	8,09	1,38
5,62	9,66	3,77	8,68	1,72	4,98	1,83	3,09
6,96	8,04	6,46	2,34	8,67	8,64	1,33	7,08
0,35	8,29	8,7	0,51	7,12	3,78	6,07	7,52
6,01	4,06	0,49	7,98	6,88	8,32	2,93	2,97

Построить интервальную группировку данных по шести интервалам равной длины и соответствующую гистограмму. Найти среднее время ожидания и исправленную дисперсию для выборки. Построить доверительные интервалы надежности 95% и 99% для среднего времени ожидания автобуса.

Решение:

Имеем выборку из = 40 элементов, Xmin = 0,27

Xmax = 9,66

Длина интервала h = = = 1,565

Получим группировки по интервалам

№ номер интервала	Левая граница	Правая граница	Частота
1	0,27	1,835	9
2	1,835	3,4	4
3	3,4	4,965	5
4	4,965	6,53	5
5	6,53	8,095	8
6	8,095	9,66	9

По формулам определим

Pi = - относительную частоту и плотность относительной частоты

P =

P1 = 9/40 = 0,225 P*1 = 0,14

P2 = 4/40 = 0,1 P*2 = 0,064

P3 = 5/40 = 0,125 P*3 = 0,08

P4 = 5/40 = 0,125 P*4 = 0,08

P5 = 8/40 = 0,2 P*5 = 0,128

P6 = 9/40 = 0,225 P*6 = 0,14

Гистограмма частот:



Найдем среднее время ожидания нужного автобуса

Хв = ,

Где X - середина интервала.

№интервала	Левая граница	Правая граница	Частота	Середина Интервалов Х	X Pi	(X - - Xв)2 Pi
1	0,27	1,835	9	1,0525	0,237	3,926
2	1,835	3,4	4	2,6175	0,262	0,682
3	3,4	4,965	5	4,1825	0,553	0,137
4	4,965	6,53	5	5,7475	0,718	0,034
5	6,53	8,095	8	7,3125	1,4625	0,868
6	8,095	9,66	9	8,8775	1,997	2,994
					5,2295	8,641

Выборочное среднее Хв = 5,2295

Выборочная дисперсия

Дв = (X - Xв)2Pi

Дисперсия Дв = 8,641

Среднее квадратичное отклонение
= = 2,94.

Исправленная выборочная дисперсия

S2 = Дв, S2 = 8,641 8,863

Исправленное квадратичное отклонение 2,98.

Построим доверительные интервалы

Хв - t < m < Хв + t

Надежность 95%, т.е. = 0,95,

= 0,475, тогда t = 1,96

5,2295 - *1,96 < m < 5,2295 + *1,96

5,2295 – 0,9242 < m < 5,2295 + 0,9242

4,3053 < m < 6,1537

Надежность 99%, т.е. = 0,99

(t) = 0,495, t = 2,58

5,2295 - *2,58 < m < 5,2295 + *2,58

5,2295 – 1,2165 < m < 5,2295 + 1,2165

4,013 < m < 6,446