Высшая математика. Кр_высшка_1к_сокр. Решение Сначала преобразуем функцию и найдем производную Задание Вычислить производную функции Решение
 Скачать 397.47 Kb. Скачать 397.47 Kb.
|
|
Задание 1. Вычислить производную функции: 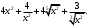 Решение: Сначала преобразуем функцию и найдем производную: 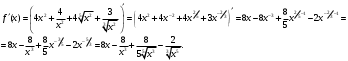 Задание 2. Вычислить производную функции: 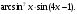 Решение: Производная находится по формуле произведения 2х функций: 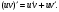 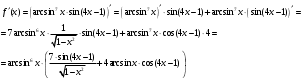 Задание 3. Вычислить производную функции: 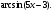 Решение: Находится как производная сложной функции: 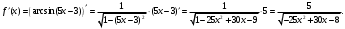 Задание 4. Вычислить производную функции: 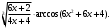 Решение: Производная находится по формуле произведения 2х функций: 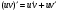 и производная сложной функции: и производная сложной функции: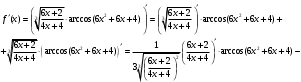  Задание 5. К графику функции 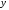 в точке в точке 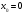 проведена касательная. Найти площадь треугольника, который отсекает эта касательная от координатного угла. проведена касательная. Найти площадь треугольника, который отсекает эта касательная от координатного угла. Решение: Напишем уравнение касательной графику функции  в точке в точке  . .Найдем производную данной функции: 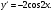 Вычислим значения производной Вычислим значения производной 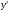 и самой функции и самой функции  в точке в точке  и получим: и получим: 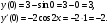 Подставим эти величины в уравнение касательной 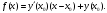 Получим: Получим: 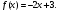 Касательная пересекает ось OY в точке C(0; 3). Найдем точку пересечения касательной с осью OX: 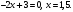 B(1,5; 0). B(1,5; 0).Введем обозначения  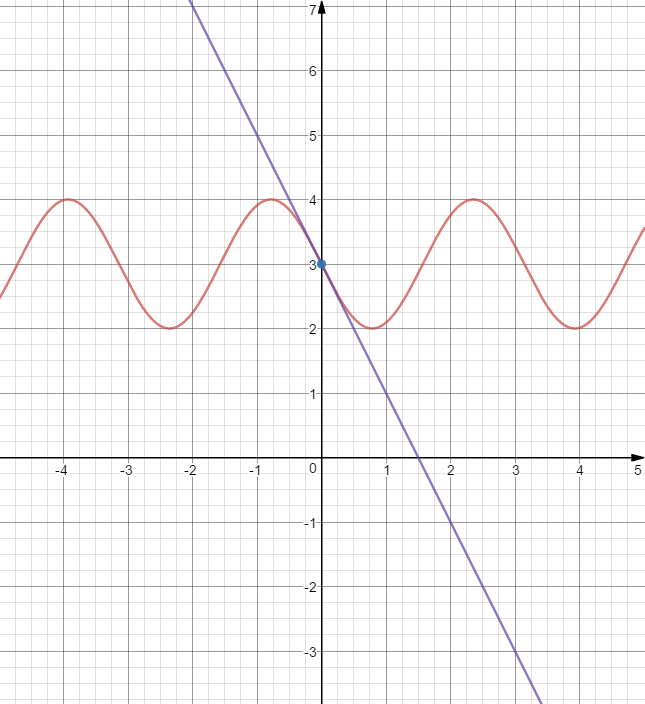 A C B Площадь треугольника вычисляется следующим образом: 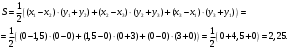 Задание 6. Вычислить   Решение:  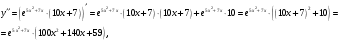 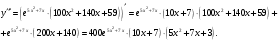 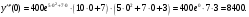 Задание 7. Найти предел, используя правило Лопиталя:  Решение:  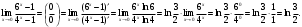 Задание 8. Найти длину интервала убывания функции 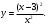 Решение: Функция определена и непрерывна на всей числовой прямой кроме точки 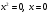 , область определения: , область определения: 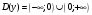 . .Найдем первую производную и решим уравнение 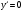 : : 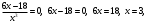 Получили критическую точку 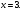 Определим знаки 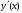 на числовой прямой: на числовой прямой: Функция возрастает на 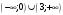 и убывает на и убывает на 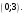 Длина интервала убывания находим как разность ее правой и левой границы: 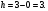 Задание 9. Найти сумму значений функции  в точках ее локального минимума и максимума: в точках ее локального минимума и максимума:  Решение: Функция определена и непрерывна на всей числовой прямой кроме точки 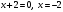 , область определения: , область определения: 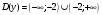 . .Для нахождения критических точек, вычислим первую производную и решим уравнение 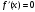 : :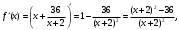 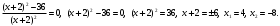 Получили критическую точки  Определим знаки  на числовой прямой: на числовой прямой: x Функция убывает на 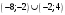 и возрастает на и возрастает на 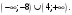 При этом 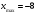 – точка локального максимума, – точка локального максимума, 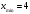 – точка локального минимума. – точка локального минимума.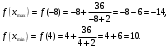 Таким образом, сумма значений функции  в точках ее локального минимума и максимума равна: в точках ее локального минимума и максимума равна:  Задание 10. Найти наибольшее и наименьшее значение функции на заданном отрезке:  Решение: Находим критические точки: 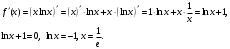 В интервал 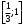 попадает корень попадает корень 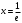 . .Находим значение функции в точке 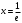 и на границах интервала: и на границах интервала: Значит, наибольшее значение функции  , наименьшее значение ‑ , наименьшее значение ‑ 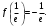 Задание 11. Издержки производства некоторого товара равны C, спрос на товар определяется функцией Pспр. Найти максимальное значение прибыли. 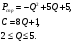 Решение: Суммарная прибыль равна разности суммарной выручки и издержек. 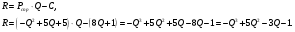 Предельная прибыль принимает вид: 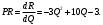 Приравнивая производную прибыли к нулю, получаем уравнение: 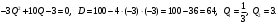 В ограничение  попадает корень попадает корень 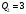 . .Найдем максимальную прибыль на интервале  Максимальная прибыль достигается при 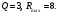 Задание 12.Вычислить интеграл: 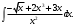 Решение: 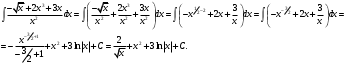 Задание 13. Вычислить интеграл: 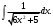 Решение: 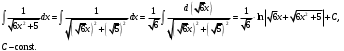 Задание 14. Найти неопределенный интеграл: 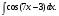 Решение: 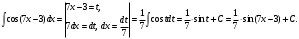 Задание 15. Вычислить интеграл: 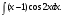 Решение: Вычислим интеграл при помощи формулы интегрирования по частям: 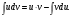 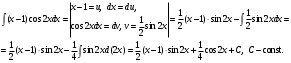 Задание 16. Найти неопределенный интеграл: 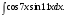 Решение: Преобразуем подинтегральную функцию используя формулу:   Задание 17. Найти неопределенный интеграл: 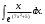 Решение: Вычислим с помощью замены: 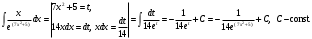 Задание 18. Найти неопределенный интеграл:  Решение: Вычислим с помощью замены:  Задание 19. Найти площадь фигуры, ограниченной линиями: 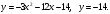 Решение: Находим точки пересечения линий. Для этого приравняем правые части уравнений: 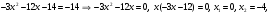 т.е. точки пересечения 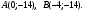 Строим заданные линии на плоскости XOY: 1) точки пересечения параболы 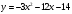 с осью OX: с осью OX: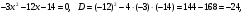 значит точек пересечения нет. значит точек пересечения нет.График функции 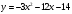 пересекает ось OY в точке пересекает ось OY в точке 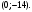 2) построим график функций и получим область, ограниченную линиями, площадь которой необходимо вычислить; 3) составляем определенный интеграл: 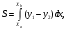 где линия 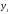 ‑ линия, ограничивающая область сверху; ‑ линия, ограничивающая область сверху; 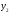 ‑ линия, ограничивающая область снизу; ‑ линия, ограничивающая область снизу; 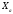 ‑ наименьшее значение переменной ‑ наименьшее значение переменной  в области; в области; 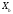 ‑ наибольшее значение переменной x в области. ‑ наибольшее значение переменной x в области. y 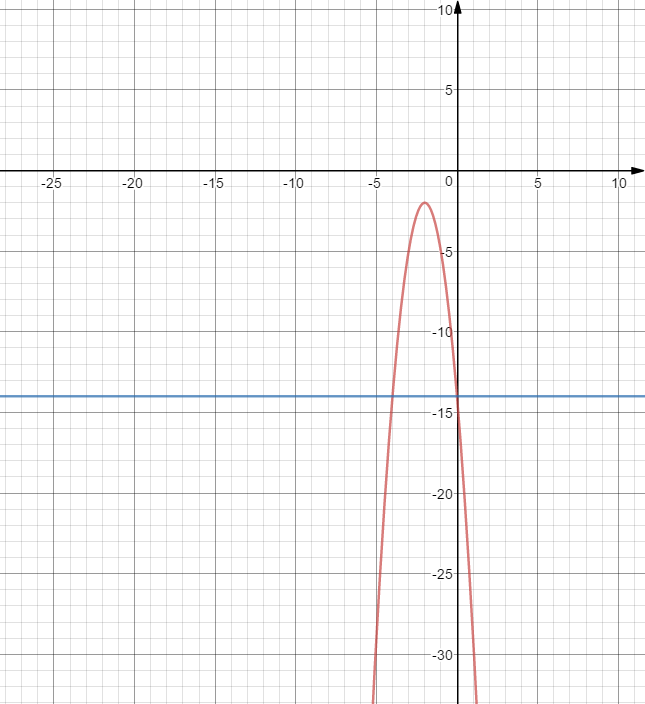           x  Задание 20. Найти площадь фигуры, ограниченной линиями: 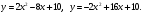 Решение: Находим точки пересечения линий. Для этого приравняем правые части уравнений: 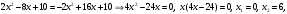 т.е. точки пересечения 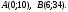 Строим заданные линии на плоскости XOY: 1) точки пересечения параболы  с осью OX: с осью OX: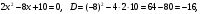 значит точек пересечения нет. значит точек пересечения нет.Точки пересечения параболы 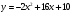 с осью OX: с осью OX: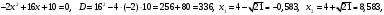 значит точки значит точки 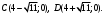 2) построим 2 параболы и получим область, ограниченную линиями, площадь которой необходимо вычислить; 3) составляем определенный интеграл: 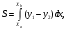 где линия 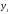 ‑ линия, ограничивающая область сверху; ‑ линия, ограничивающая область сверху; 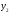 ‑ линия, ограничивающая область снизу; ‑ линия, ограничивающая область снизу; 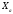 ‑ наименьшее значение переменной ‑ наименьшее значение переменной  в области; в области; 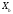 ‑ наибольшее значение переменной x в области. ‑ наибольшее значение переменной x в области. 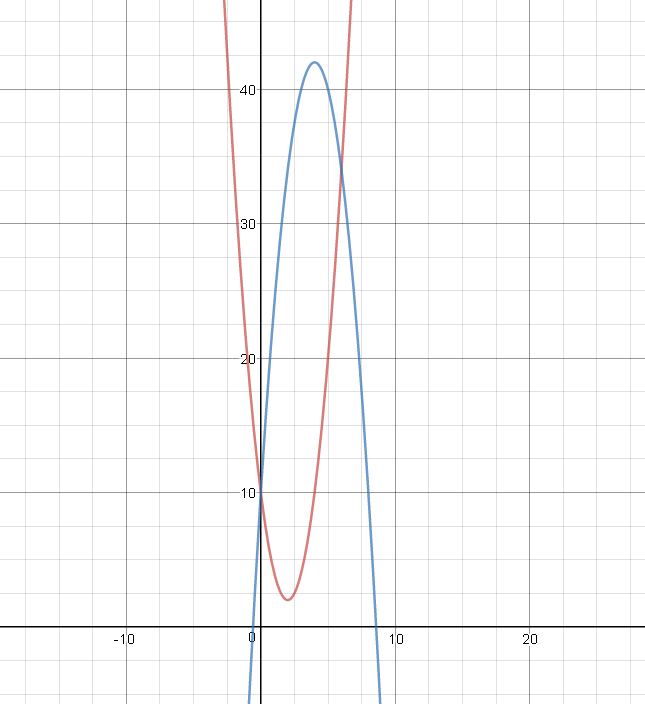                     x y 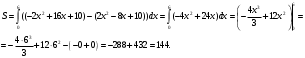 |
