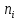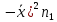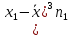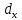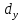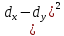Математический метод. Решение. Упорядочим значения по возрастанию, получим ряд 5
 Скачать 103.59 Kb. Скачать 103.59 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Математические методы в психологииГруппа ПК19П161 Студент Камилла Дилмурадовна Абдуманнопова МОСКВА 2022 Задание №1. Дана выборка: 10, 20, 20, 5, 15, 20, 5, 10, 20, 5. Требуется: а) построить статистический ряд распределения частот и полигон частот; б) построить вариационный ряд; в) найти дисперсии; г) найти выборочные моду, медиану, коэффициент вариации, коэффициент асимметрии. Решение. Упорядочим значения по возрастанию, получим ряд:
Найдем количество вхождений каждого значения, получим ряд распределения частот, по которому построим полигон частот.
 Найдем оценки математического ожидания и дисперсии. Найдем выборочное среднее: 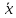 = =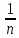 ∑ ∑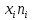 = =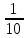 130=13 130=13Найдем исправленную дисперсию (несмещенную оценку для дисперсии по выборке): 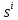 = =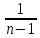 ∑( ∑(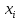 - -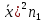 = =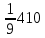 ≈45,556. ≈45,556.Найдем исправленное среднее квадратическое отклонение s ≈ 6,749. Промежуточные вычисления приведены в таблице ниже:
Найдем выборочные моду, медиану, коэффициент вариации, коэффициент асимметрии. Мода – значение с наибольшей частотой, Mo = 20. Медиана – значение в середине ряда, в данном случае среднее арифметическое двух серединных значений: Me=1=12, 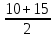 . .Коэффициент вариации 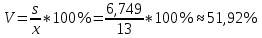 Коэффициент асимметрии 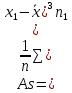 Ответ: дисперсия – 45,556; мода – 20; медиана – 12,5; коэффициент вариации – 51,92%; коэффициент асимметрии – -0,068. Задание 2. Дан следующий вариационный ряд:
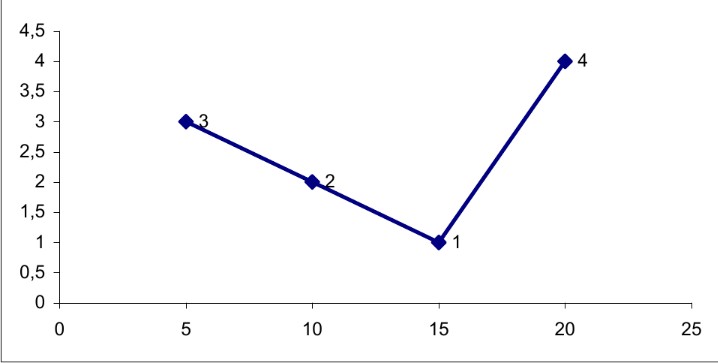
Требуется: 1) Построить полигон распределения 2) Вычислить выборочную среднюю, дисперсию, моду, медиану Ответ: 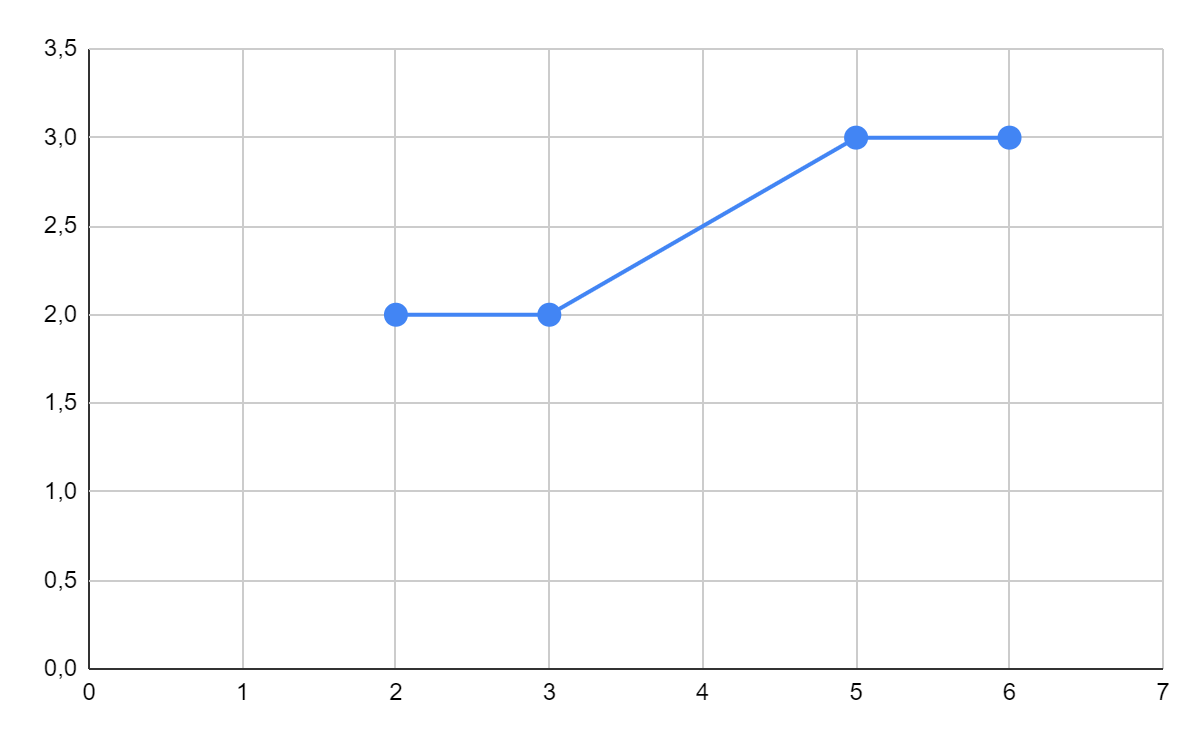 Выборочная средняя: 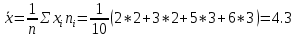 = = Выборочная дисперсия: 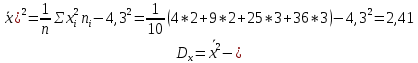 Мода: Mo = 5;6 Медиана: Me = 4 Задание №3. У 24 девушек – студентов физического и психологического факультетов был измерен уровень вербального интеллекта по методике Векслера. Можно ли утверждать, что одна из групп превосходит другую по уровню вербального интеллекта? Физики: 123, 134, 126, 131, 134, 132, 126, 132, 127, 127, 136, 133, 136, 135, Психологи: 123, 125, 132, 120, 127, 126, 120, 126, 120, 119, Ответ: Используем критерий Q Розенбаума. Упорядочим значения в обеих выборках, а затем сформулируем гипотезы: H0: Студенты-физики не превосходят студентов-психологов по уровню вербального интеллекта. H1: Студенты-физики превосходят студентов-психологов по уровню вербального интеллекта.
Определяем количество значений первого ряда, которые больше максимального значения второго ряда: 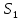 =6. =6. Теперь определяем количество значений второго ряда, которые меньше минимального значения первого ряда: 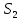 =4. =4. Вычисляем 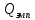 по формуле: по формуле: 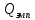 = S1+S2 = 6+4 = 10. = S1+S2 = 6+4 = 10. Определяем критические значения Q для 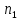 =14, =14, 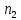 =10. =10. 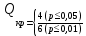 Ясно, что чем больше расхождения между выборками, тем больше величина Q. Но отклоняется при 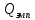 > >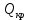 , а при , а при 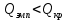 мы будем вынуждены мы будем вынужденыпринять Но. Студенты-физики не превосходят студентов психологов по уровню вербального интеллекта (р<0,05). Задание №4. Психолог просит супругов проранжировать девять личностных черт, имеющих определяющее значение для семейного благополучия. Задача заключается в том, чтобы определить, в какой степени совпадают оценки супругов по отношению к ранжируемым качествам. Заполните таблицу и, посчитав коэффициент ранговой корреляции Спирмена, ответьте на поставленный вопрос.
По формуле вычисляем коэффициент ранговой корреляции Спирмена. 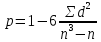 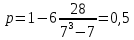 Ответ: Согласованность между мнениями супругов прямая и сильная. |