Исследование функции. Исследуем функцию. Исследуем функцию, заданную формулой 1 Область определения множество всех действительных чисел
 Скачать 90.52 Kb.
|
|
Исследуем функцию, заданную формулой:  1) Область определения: множество всех действительных чисел Данная функция определена для: 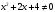  2) Проверим функцию на нечетность:  То есть, функция не является нечетной и не является четной. 3) Точки пересечения с осями координат: Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю.  Дробь обращается в нуль тогда, когда числитель равен нулю.  Перенесем известные величины в правую часть уравнения.  Точки пересечения с осью : Пусть 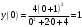 Точки пересечения с осью : 4) Вертикальных асимптот нет, т.к. функция определена на всей числовой прямой.  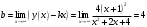 То есть, имеем горизонтальную асимптоту:  Наклонной асимптоты нет. 5) Найдем первую производную функции, воспользовавшись формулой производной частного и приравниваем к нулю 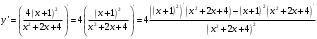   Для нахождения критических точек приравняем первую производную к нулю и решим полученное уравнение. Дробь обращается в нуль тогда, когда числитель равен нулю. Вторая производная: 6) Точки перегиба 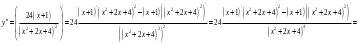    Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение.  Дробь обращается в нуль тогда, когда числитель равен нулю. 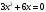    .Тестовые интервалы:  7) Результаты исследования функции занесем в таблицу.
Относительные экстремумы: Проходя через точку минимума, производная функции меняет знак с (-) на (+). Относительный минимум  .Данные таблицы нанесем на координатную плоскость. Используя результаты исследования функции, построим ее график.  |