Контрольная работа Техническая механика. Контрольная работа По дисциплине Техническая механика Тема Вариант 8 Абрамчик Татьяна Николаевна студент 2 курса группы
 Скачать 4.19 Mb. Скачать 4.19 Mb.
|
|
МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ им. В.Г.ШУХОВА» (БГТУ им. В.Г. Шухова) Кафедра (Русского языка) Контрольная работа По дисциплине: Техническая механика Тема: «Вариант __8___ Выполнил: Абрамчик Татьяна Николаевна студент 2 курса группы ЭКзд-211 Института заочного образования Проверил: Белгород, 2023 Содержание:Введение 2 Задача №1. 4 Задача №2. 5 Задача №3. 7 Задача №4. 10 Задача 5 14 Задача 6 18 Задача 7 20 но на Список использованной литературы: 22 Введение1. Техническая механика – дисциплина, вмещающая в себя основные механические дисциплины: теоретическую механику, сопротивление материалов, теорию машин и механизмов, детали машин и основы конструирования. Техническая механика – это наука, изучающая общие законы механического движения и механического взаимодействия материальных тел. Основные понятия и аксиомы статики Техническая механика — комплексная дисциплина. Она включает три раздела: «Техническая механика», «Сопротивление материалов», «Детали машин». « Техническая механика» — раздел, в котором излагаются основные законы движения твердых тел и их взаимодействия. В разделе «Сопротивление материалов» изучаются основы прочности материалов и методы расчетов элементов конструкций на прочность, жесткость и устойчивость под действием внешних сил. В заключительном разделе «Технической механики» «Детали машин» рассматриваются основы конструирования и расчета деталей и сборочных единиц общего назначения. Дисциплина «Техническая механика» является общепрофессиональной, обеспечивающей базовые знания при усвоении специальных дисциплин, изучаемых в дальнейшем. Задачи технической механики: Техническая механика наука о механическом движении материальных твердых тел и их взаимодействии. Механическое движение понимается как перемещение тела в пространстве и во времени по отношению к другим телам, в частности к Земле. Для удобства изучения техническую механику подразделяют на статику, кинематику и динамику. Статика изучает условия равновесия тел под действием сил. Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются. Динамика изучает движение тел под действием сил. В отличие от физики техническая механика изучает законы движения некоторых абстрактных абсолютно твердых тел: здесь материалы, форма тел существенного значения не имеют. При движении абсолютно твердое тело не деформируется и не разрушается. В случае, когда размерами тела можно пренебречь, тело заменяют материальной точкой. Это упрощение, принятое в технической механике, значительно облегчает решение задач о движении. Задача №1.Груз подвешен на стержнях и канатах и находится в равновесии (рис. 1.13). Изобразить систему сил, действующих на шарнир 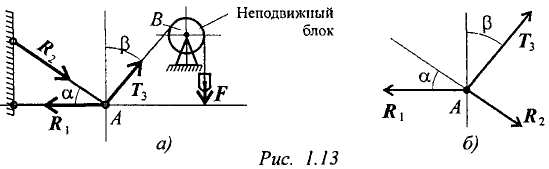 Решение: Реакции стержней направлены вдоль стержней, реакции гибких связей направлены вдоль нитей в сторону натяжения (рис. 1.13а). Для определения точного направления усилий в стержнях мысленно убираем последовательно стержни 1 и 2. Анализируем возможные перемещения точки Убираем стержень 1. точка Убираем стержень 2, точка Канат тянет вправо. Освобождаемся от связей (рис. 1.136). Задача №2.Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях (рис. 2.5а). Решение: Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис. 2.5а). Определяем возможные направления реакций связей «жесткие стержни». 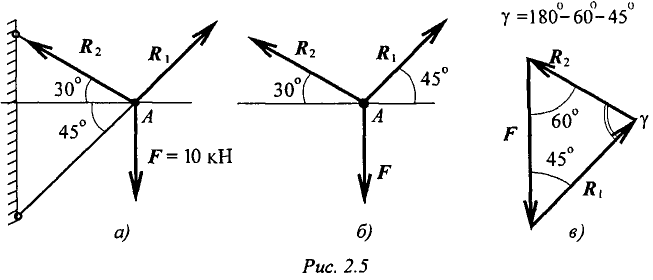 Усилия направлены вдоль стержней. Освободим точку Система находится в равновесии. Построим треугольник сил. Построение начнем с известной силы, вычертив вектор Из концов вектора Пересекаясь, линии создадут треугольник (рис. 2.5в). Зная масштаб построений и измерив длину сторон треугольника, можно определить величину реакций в стержнях. Для более точных расчетов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла — величина постоянная 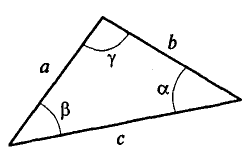 Для данного случая: 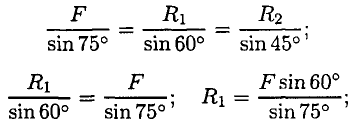 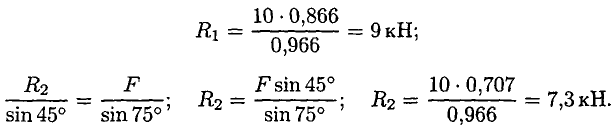 Замечание. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону. Задача №3.Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях (рис. 2.6а). Решение: 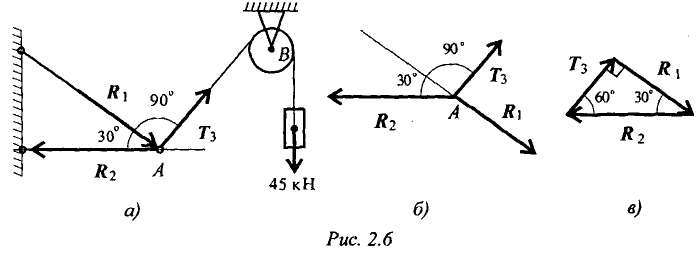 Нанесем на схему возможные направления усилий, приложенных в точке Груз находится в равновесии, следовательно, в равновесии находится точка Освободим точку Замечание. Рассмотрим только силы, приложенные к точке Строим треугольник для сил, приложенных в точке Образовался прямоугольный треугольник (рис. 2.6в). Неизвестные реакции стержней можно определить из соотношений в прямоугольном треугольнике: 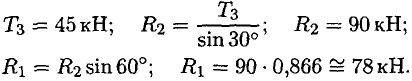 Замечание. При равновесии векторы сил в треугольнике направлены один за другим (обходим треугольник по часовой стрелке). Сравним направления сил в треугольнике с принятыми в начале расчета на рис. 1.26а. Направления совпали, следовательно, направления реакций определены верно. Задача №4.
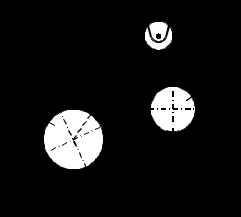
Решение: 1. Решим задачу аналитически. Для этого рассмотрим равновесие шара 1. На него действует реакция N опорной поверхности А, перпендикулярная к этой поверхности; сила натяжения Т1 нити и вес Р1 шара 1 (рис. 2). 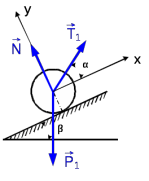 Рис. 2 Уравнения проекций всех сил, приложенных к шару 1, на оси координат имеют вид: 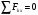 : : 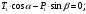 (1) (1)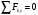 : : 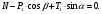 (2) (2)Из уравнения (1) находим силу натяжения Т1 нити: 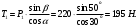 Тогда из уравнения (2) определим реакцию N опорной поверхности: 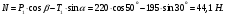 Теперь рассмотрим равновесие шара 2. На него действуют только две силы: сила натяжения Т2 нити и вес Р2 этого шара (рис. 3). 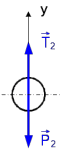 Рис. 3 Поскольку в блоке Д трение отсутствует, получаем 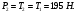 2. Решим задачу графически. Строим силовой треугольник для шара 1. Сумма векторов сил, приложенных к телу, которое находится в равновесии, равна нулю, следовательно, треугольник, составленный из 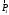 , , 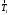 и и 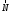 должен быть замкнут (рис. 4). должен быть замкнут (рис. 4).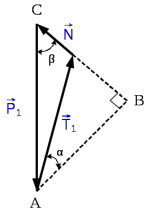 Рис. 4 Определим длины сторон силового треугольника по теореме синусов: 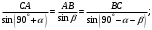 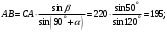 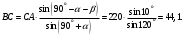 Тогда искомые силы равны: 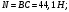 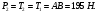 Задача 5
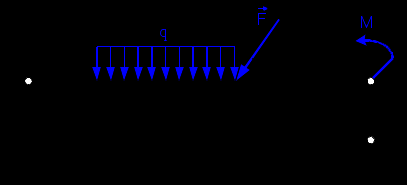
Решение 1. Рассмотрим равновесие балки АВ. На неё действует равнодействующая Q распределённой на отрезке ЕК нагрузки интенсивности q, приложенная в середине этого отрезка; составляющие XA и YA реакции неподвижного шарнира А; реакция RС стержня ВС, направленная вдоль этого стержня; нагрузка F, приложенная в точке К под углом 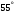 ; пара сил с моментом М (рис. 6). ; пара сил с моментом М (рис. 6).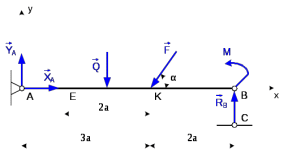 Рис. 6 2. Равнодействующая распределенной нагрузки равна: 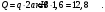 3. Записываем уравнение моментов сил, приложенных к балке АВ, относительно точки А: 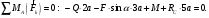 (3) (3)4. Уравнения проекций всех сил на оси координат имеют вид: 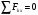 : : 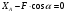 , (4) , (4)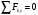 : : 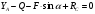 , (5) , (5)Из уравнения (3) находим реакцию RС стержня ВС: 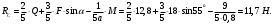 По уравнению (4) вычисляем составляющую XA реакции неподвижного шарнира А: 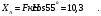 С учетом этого, из уравнения (5) имеем: 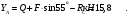 Тогда реакция неподвижного шарнира А равна: 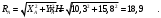 Задача 6
Решение 1. Поскольку маховик вращается равноускоренно, то точки на ободе маховика вращаются по закону: 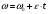 (11) (11)По условию задачи маховик в начальный момент находился в покое, следовательно, 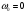 и уравнение (11) можно переписать как и уравнение (11) можно переписать как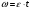 (12) (12)2. Определяем угловую скорость вращения точек обода маховика в момент времени 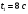 : :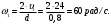 3. Находим угловое ускорение вращения маховика из уравнения (12): 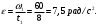 4. Вычисляем угловую скорость вращения точек обода маховика в момент времени 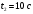 : :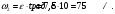 5. Тогда частота вращения маховика в момент времени 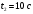 равна: равна: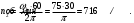 6. По формуле Эйлера находим скорость точек обода маховика в момент времени 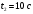 : :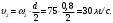 7. Определяем нормальное ускорение точек обода маховика в момент времени 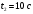 : :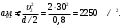 8. Находим касательное ускорение точек обода маховика в момент времени 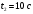 : :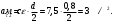 Задача 7
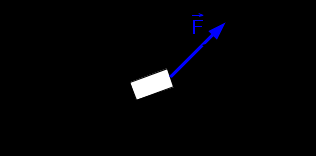
Решение 1. Работа силы F определяется по формуле: 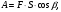 (13) (13)где 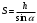 – перемещение груза. – перемещение груза.2. По условию задачи груз перемещается с постоянной скоростью, поэтому ускорение груза 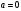 . .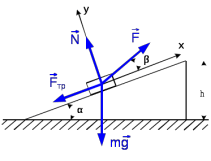 Рис. 10 3. Выбираем систему координат, направляя ось х вдоль линии движения груза. Записываем уравнения движения груза под действием сил (рис. 10): 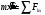 : : 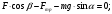 (14) (14)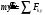 : : 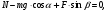 (15) (15)где 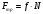 – сила трения скольжения. – сила трения скольжения.Выражаем из уравнения (14) реакцию 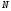 наклонной плоскости наклонной плоскости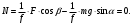 и подставляем в уравнение (15), получаем 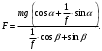 Тогда работа силы F равна 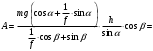 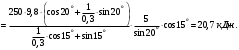 4. Мощность, развиваемая за время перемещения 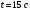 , определяется по формуле: , определяется по формуле: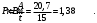 Размеще Размещено на Список использованной литературы: Аркуша А.И. Техническая механика и сопротивление материалов: Учебник для машиностроительных специальностей техникумов / А. И. Аркуша. - 2-е изд., доп. . - М.: Высшая школа, 1989. - 352 с. Никитин Е.М. Теоретическая механика для техникумов. М., 1969г., 432 с. Сетков В.И.: Сборник задач для расчетно-графических работ по технической механике: Учеб. Пособие для техникумов. 2-е изд., доп. - М.: Стройиздат, 1989,-224 с. Олофинская В.П. Техническая механика курс лекций с вариантами практических работ и тестовых заданий. М. Форум - ИНФРА-М. 2003г. 348стр. (электронная версия). |