Антенны Балагуров (1). Контрольная работа по дисциплине "Антенны и распространение радиоволн" Балагуров М. И. Группа ист11 Проверил Ищук А. А

• Название: Контрольная работа по дисциплине "Антенны и распространение радиоволн" Балагуров М. И. Группа ист11 Проверил Ищук А. А
• Дата: 02.05.2022
• Размер: 2.35 Mb.
• Имя файла: Антенны Балагуров (1).doc
• Тип: Контрольная работа; #507149
• страница: 2 из 3

Задача 1.

Определить отношение плотности тока смещения к плотности тока проводимости для морской воды с параметрами ԑ₁ = 80, µ₁ = 1 , ₁ = 8 См/м и сухой почвы с параметрами ԑ₂ = 8, µ₂ = 1, ₂ = 210^-3 См/м на частотах f₁ = (М +
+ 1)۰10⁴, f₂ = (М + 1)۰10⁶, f₃ = (М + 1)۰10⁸ Гц. Провести сравнение этих отношений для заданных сред. Определить комплексную диэлектрическую проницаемость обеих сред для указанных частот.
Решение:

Дано: N = 2, M = 8.

Тогда f₁ = (М + 1)10⁴ = (8 + 1)10⁴ = 90 кГц;

f₂ = (М + 1)10⁶ = (8 + 1)10⁶ = 9 МГц;

f₃ = (М + 1)10⁸ = (8 + 1)10⁸ = 900 МГц.

Среды могут сильно отличаться друг от друга по величине удельной проводимости, поэтому электромагнитные поля в таких средах могут обладать разными свойствами [5, стр. 35]. Чем больше величина , тем больше плотность тока проводимости в среде при той же напряженности электрического поля. Часто для упрощения анализа вводят понятия идеального проводника и идеального диэлектрика. Идеальный проводник - это среде с бесконечно большой удельной проводимостью (  ). В идеальном диэлектрике  = 0, а  и  - вещественные скалярные функции или постоянные. В идеальном проводнике может существовать только ток проводимости, а в идеальном диэлектрике - только ток смещения.

Отношение модулей плотности тока проводимости к плотности тока смещения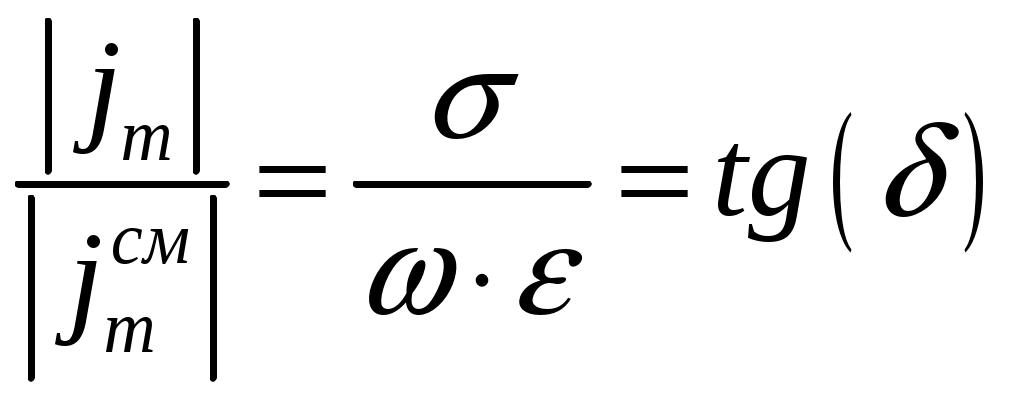

(1.1)

является критерием для деления сред на проводники и диэлектрики. Если tg() >> 1, среду называют проводником, если tg() << 1 - диэлектриком.

Комплексная диэлектрическая проницаемость среды [5, стр. 3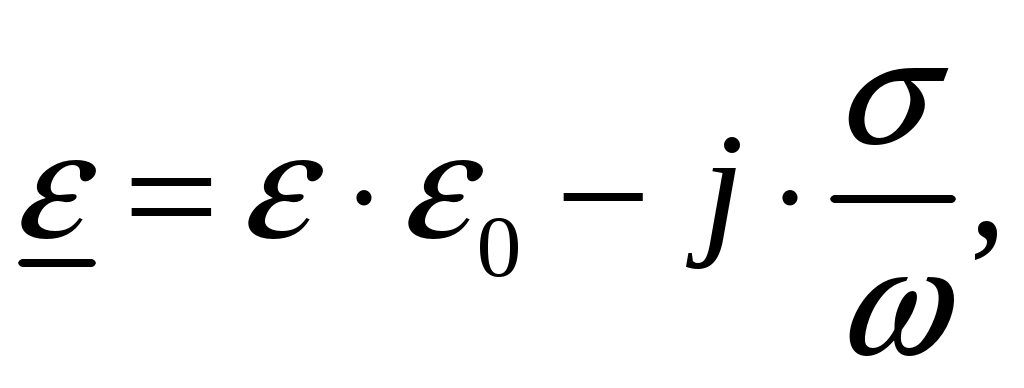2]

(1.2)

где 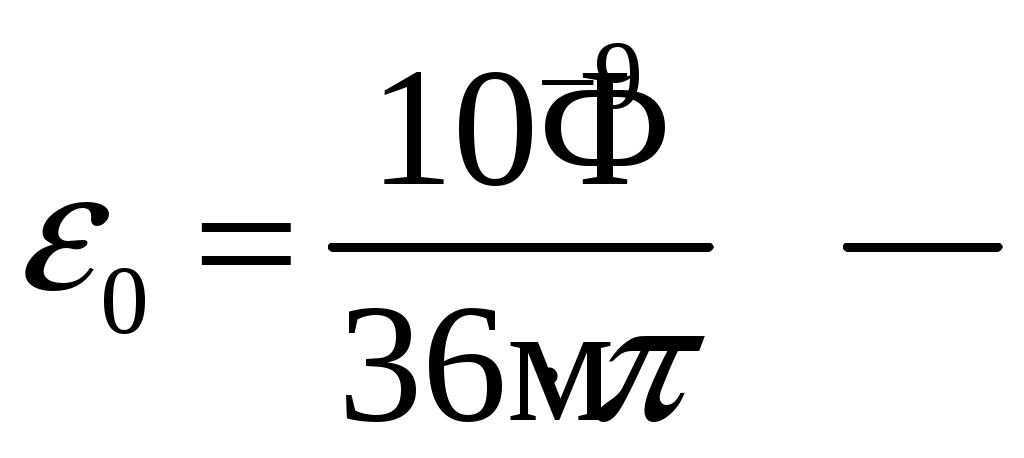 диэлектрическая проницаемость вакуума;

  проводимость среды, См/м;

 = 2f  циклическая частота, рад/с.

Выполним расчеты для морской воды с параметрами ԑ₁ = 80, µ₁ = 1, ₁ = 8 См/м.

f₁ = 90 кГц: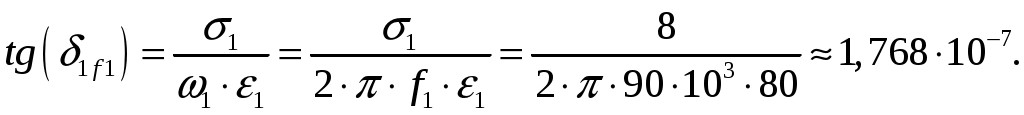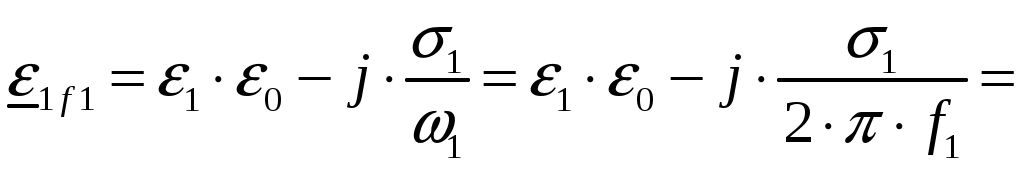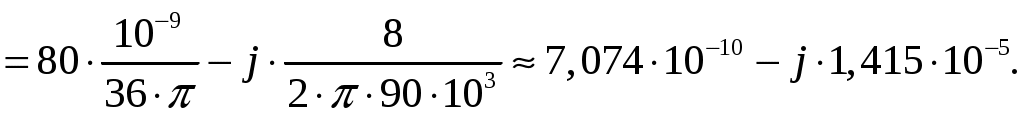



среда является диэлектриком.





f₂ = 9 МГц: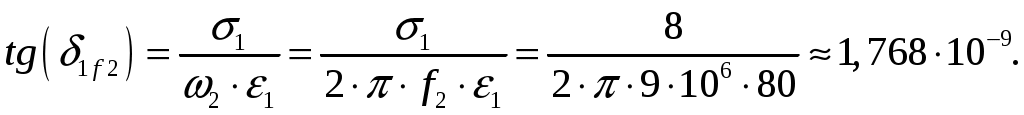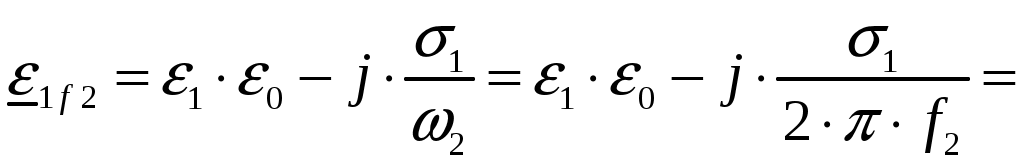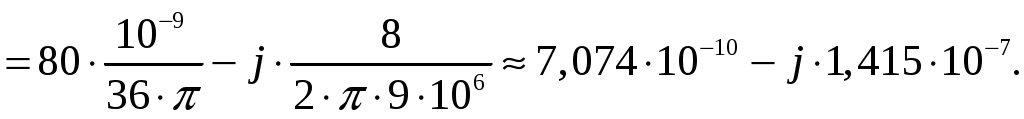



среда является диэлектриком.





f₃ = 900 МГц: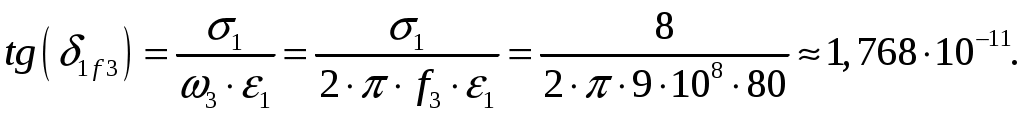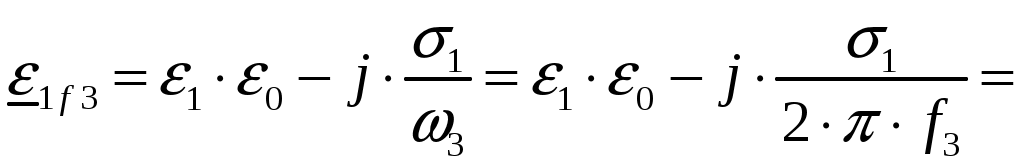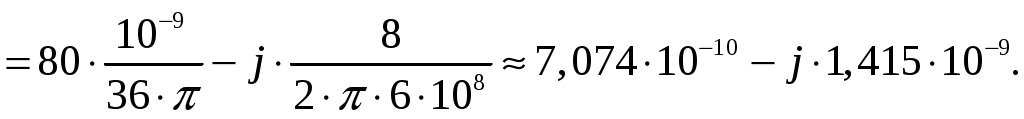



среда является диэлектриком.





Выполним расчеты сухой почвы с параметрами ԑ₂ = 8, µ₂ = 1, ₂ = 210^-3 См/м.

f₁ = 90 кГц: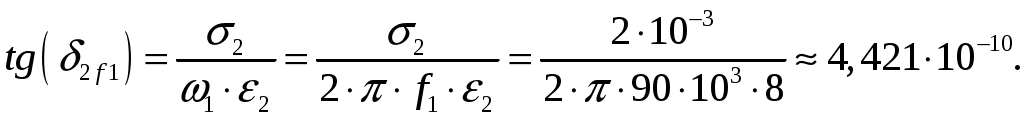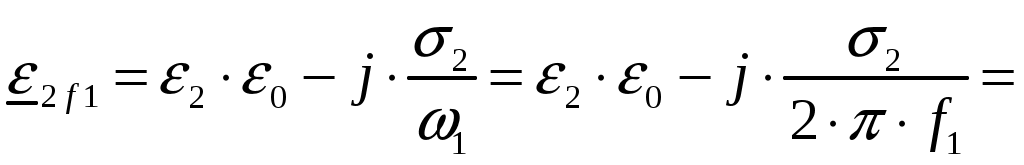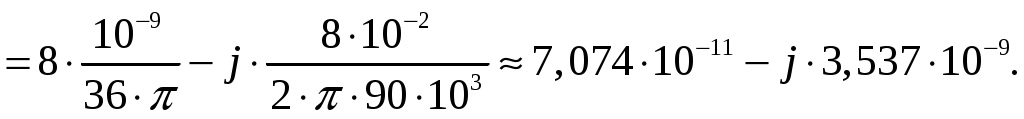



среда является диэлектриком.





f₂ = 9 МГц: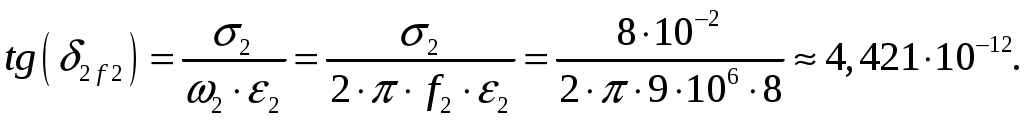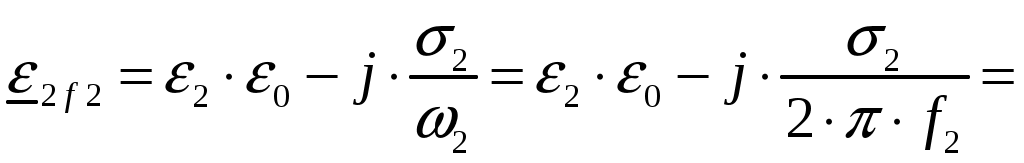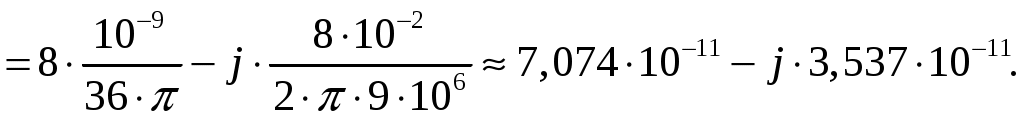



среда является диэлектриком.





f₃ = 900 МГц: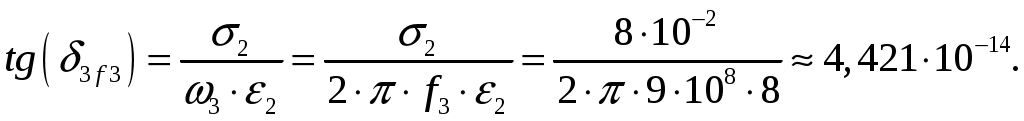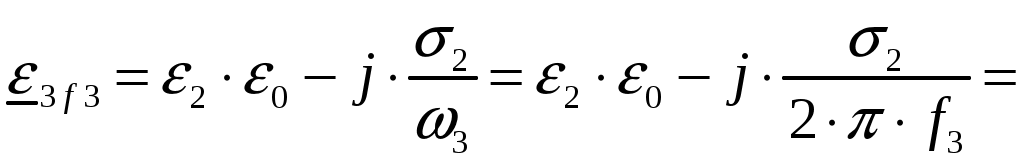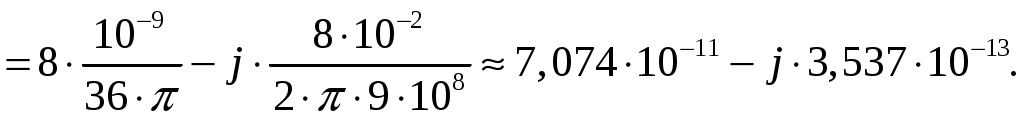



среда является диэлектриком.




Ответ: Определены отношение плотности тока смещения к плотности тока проводимости для морской воды с параметрами ԑ₁ = 80, µ₁ = 1 , ₁ = 8 См/м:

на частоте f₁ = 90 кГц: , среда является диэлектриком, комплексная диэлектрическая проницаемость равна



на частоте f₂ = 9 МГц: среда является диэлектриком, комплексная диэлектрическая проницаемость равна



на частотеf₃ = 900 МГц: среда является диэлектриком, комплексная диэлектрическая проницаемость равна



для сухой почвы с параметрами ԑ₂ = 8, µ₂ = 1, ₂ = 210^-3 См/м:

на частоте f₁ = 90 кГц: , среда является диэлектриком, комплексная диэлектрическая проницаемость равна



на частоте f₂ = 9 МГц: , среда является диэлектриком, комплексная диэлектрическая проницаемость равна



на частотеf₃ = 600 МГц: , среда является диэлектриком, комплексная диэлектрическая проницаемость равна



Сравнивая полученные отношение плотности тока смещения к плотности тока проводимости получаем, что на заданных частотах и морская вода, и сухая почва являются диэлектриками. Отличие наблюдается в значениях tg() и в комплексных диэлектрических проницаемостях среды:

- у сухой почвы tg() в 400 раз больше, чем у морской воды, причем это справедливо для всех частот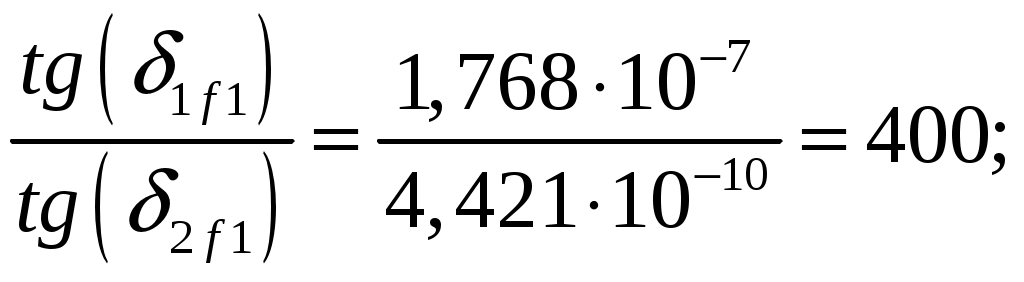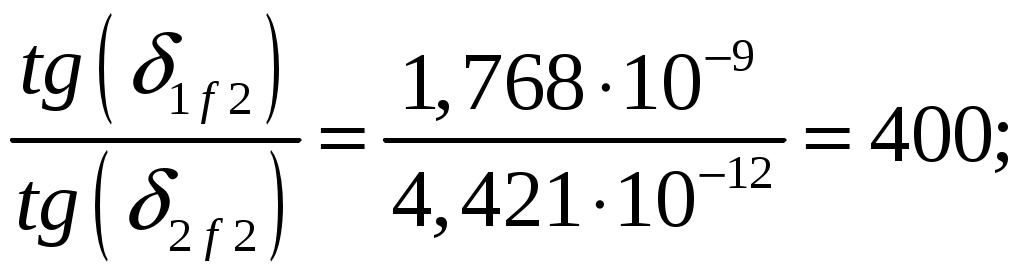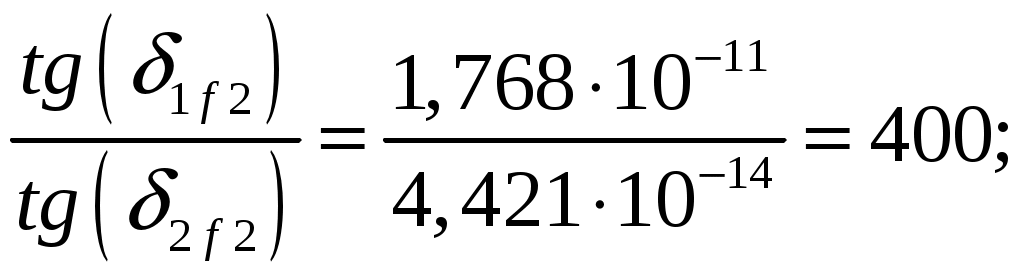





- у сухой почвы действительная часть комплексной диэлектрической проницаемости в 10 раз больше, чем у морской воды, причем это справедливо для всех частот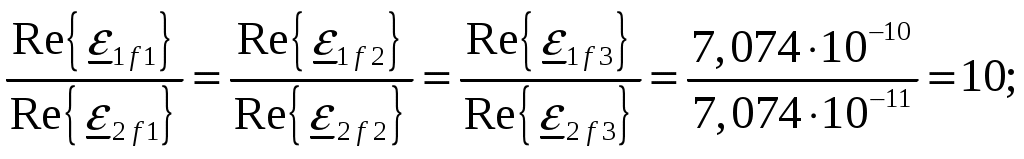



- у сухой почвы мнимая часть комплексной диэлектрической проницаемости в 4000 раз больше, чем у морской воды, причем это справедливо для всех частот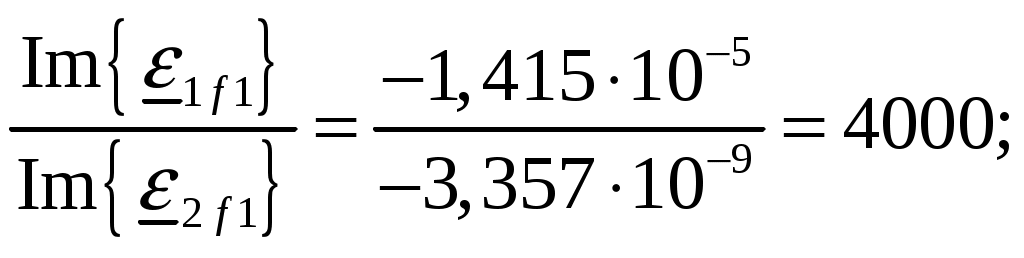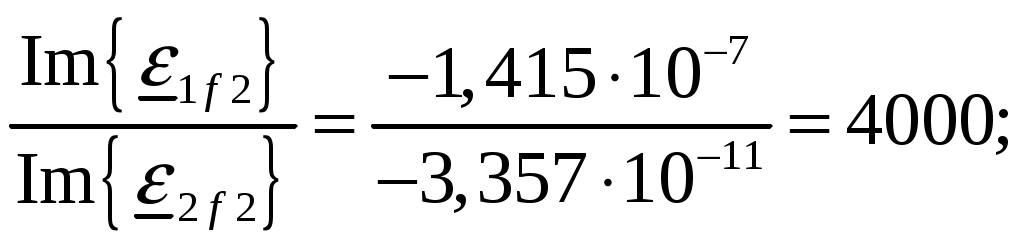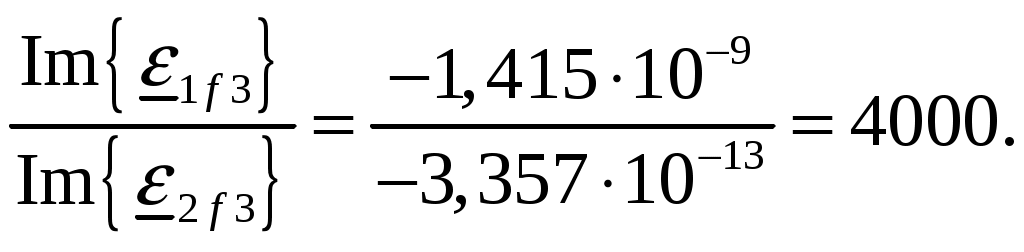





В пределах одной среды с увеличением частоты tg() уменьшается обратно пропорционально частоте, действительная часть комплексной диэлектрической проницаемости не изменяется, а мнимая часть комплексной диэлектрической проницаемости уменьшается обратно пропорционально частоте.
Задача 2.

Определить критическую длину волны слоя ионосферы с электронной концентрацией (2,5 + N)۰10⁵ э/см³. Определить для этого же слоя показатель преломления на частотах f₁ = (5 + М) МГц и f₂ = (20 + М) МГц, и определить фазовую скорость волны на этих частотах. Определить минимальную длину волны при падении на слой ионосферы электромагнитной волны под различными углами β = 10°, 30°,60°.
Решение:

Дано: N = 2, M = 8.

Тогда электронная концентрация

N_Э = (2,5 + N)10⁵ = (2,5 + 2)10⁵ = 4,510⁵ э/см³;

f₁ = (5 + М) = (5 + 8) = 13 МГц; f₂ = (20 + М) = (20 + 8) = 28 МГц.

Наибольшую частоту, при которой радиоволны отражаются от ионизированного слоя при вертикальном падении на него, называют критической [1, стр. 29]. Критическая частота f_КР и электронная концентрация слоя связаны уравнениями:

(2.1)

где f_КР  критическая частота, Гц;

N_Э  электронная концентрация э/м³.

N_Э = 4,510⁵ э/см³ = 4,510¹¹ э/м³.



Показатель преломления определяется по формуле [2, стр. 509]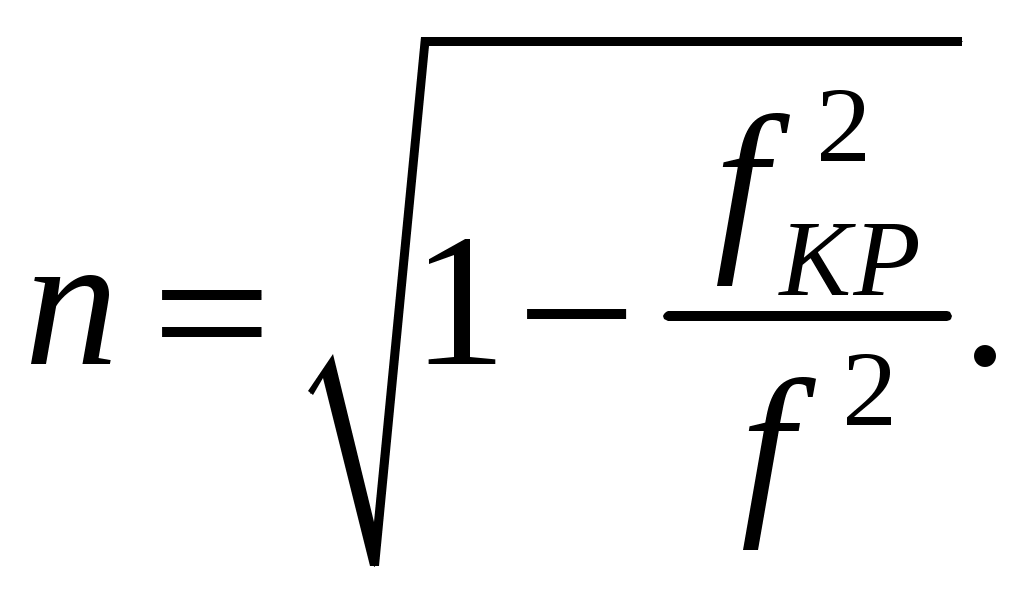

(2.2)

Подставляя численные значения, получаем:

при f₁ = 13 МГц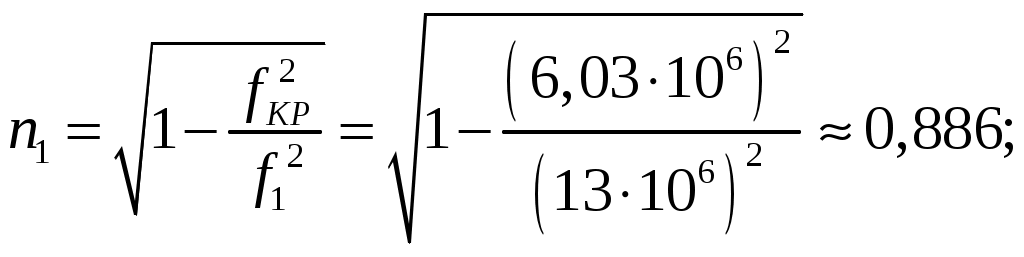



при f₂ = 28 МГц.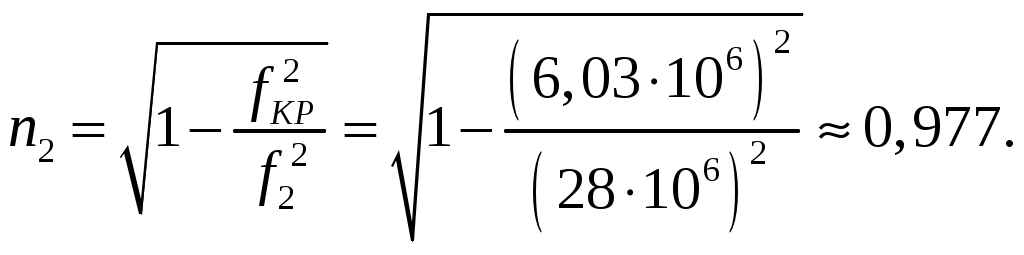



Фазовая скорость волны в среде [2, стр.]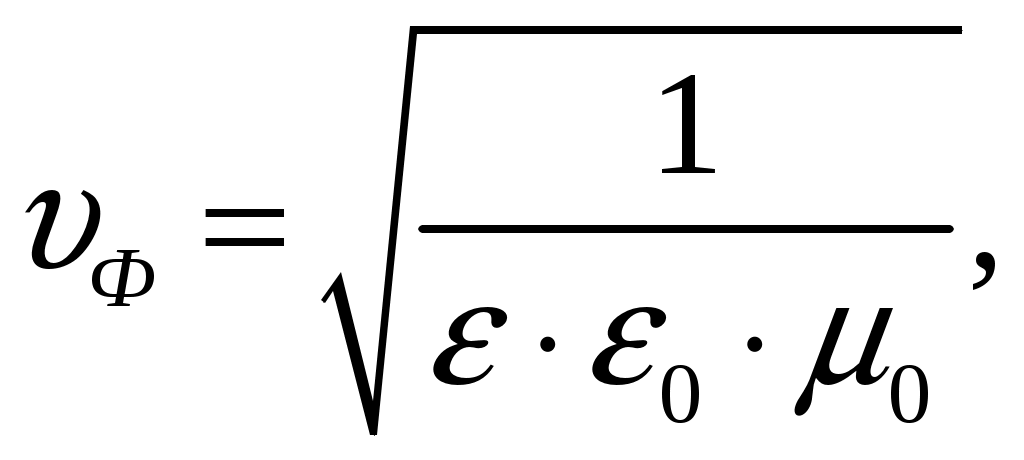

(2.3)

где 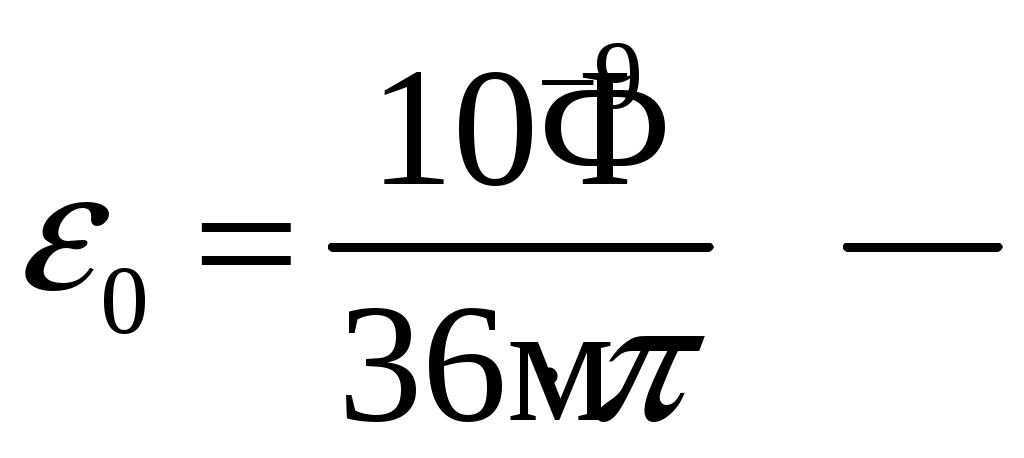 диэлектрическая проницаемость вакуума;

₀ = 410^-7 Гн/м  магнитная проницаемость вакуума.

Относительная диэлектрическая проницаемость среды

При f₁ = 13 МГц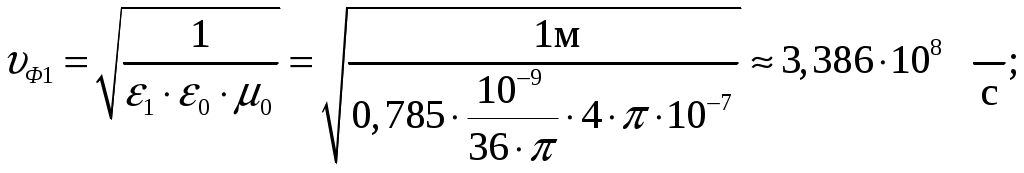





при f₂ = 28 МГц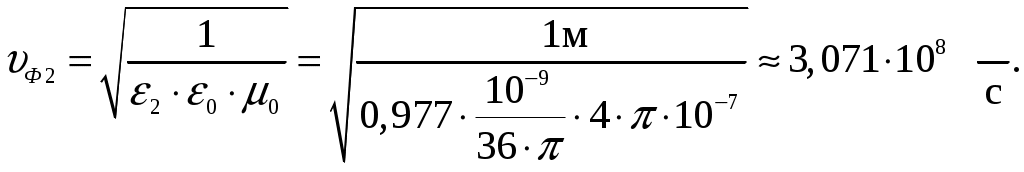





Связь между углами: центральным ; возвышения ; падения на отражающий слой  показана на рис. 2.1.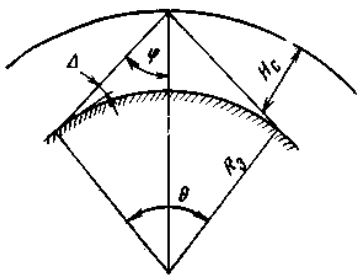





Рисунок 2.1 - Связь между углами: центральным ;
возвышения ; падения на отражающий слой 
Наибольшая частота отражается от слоя при угле излучения  = 0. Ее значение определяется уравнением

(2.4)

где R_З  радиус Земли, км, R_З = 6370 км;

Н_С  действующее значение высоты cлоя F₂, км, примем равным 300 км.

Без учета сферичности Земли и ионосферы (когда r  500 км) максимальная и критическая частоты с углом падения на отражающий слой  (рис. 2.1) связаны законом секанса:

(2.5)

Минимально применимая длина волны определится по формуле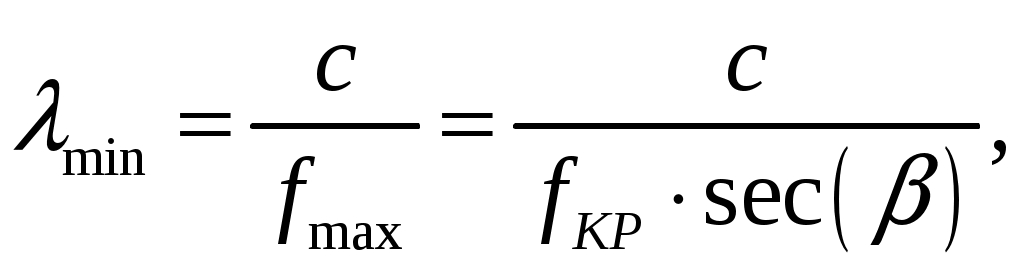

(2.6)

где c = 310⁸ м/с  скорость света.

Определим минимальную длину волны при падении на слой ионосферы электромагнитной волны под различными углами β₁ = 10°, β₂ = 30° и β₃ = 60°.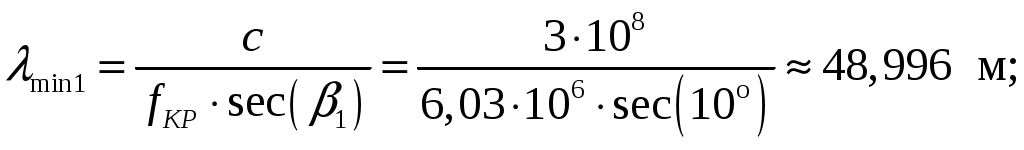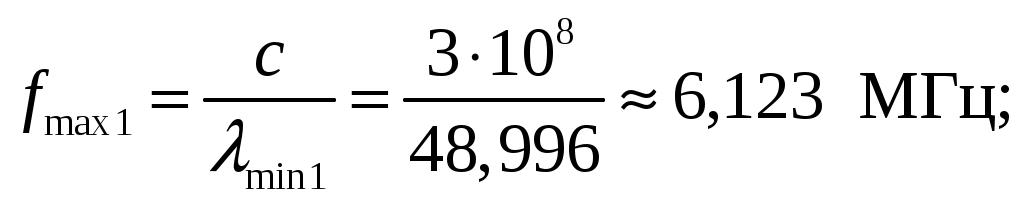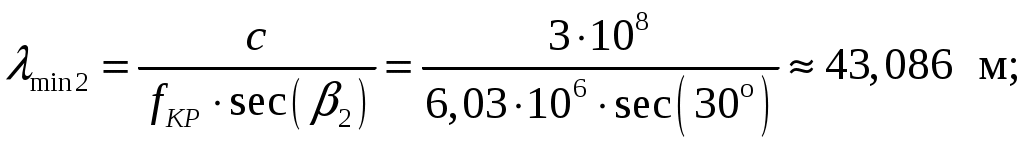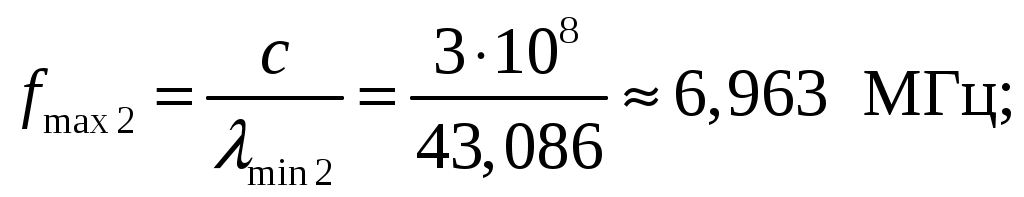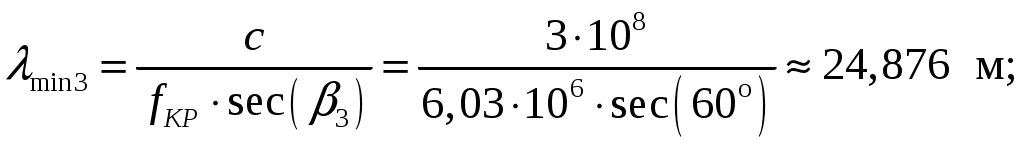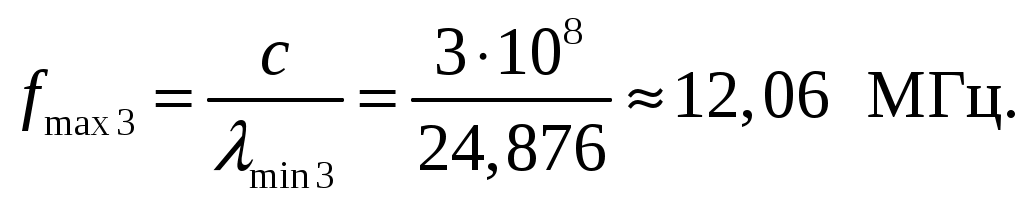












Ответ: Критическая длина волны слоя ионосферы с электронной концентрацией N_Э = 4,510⁵ э/см³. составляет f_КР = 6,03 МГц. Для этого же слоя показатель преломления на частотах f₁ = 13 МГц и f₂ = 28 МГц будут равны соответственно n₁ = 0,886 и n₂ = 0,977, а фазовые скорости волн на этих частотах будут равны _Ф1 = 3,38610⁸ м/с и _Ф2 = 3,07110⁸ м/с. При падении на слой ионосферы электромагнитной волны под различными углами β₁ = 10°, β₂ = 30° и β₃ = 60° минимальные длины волн составят соответственно _min1 =
= 48,996 м,_min2 = 43,086 м,_min3 = 24,876 м, которые будут соответствовать частотам f_max1 = 6,123 МГц;f_max2 = 6,963 МГц и f_max3 = 12,06 МГц.

Задача 3.

Передающая и приемная антенны имеют высоты h₁ = (10 + N) м,
h₂ = (10 + М) м. Определить расстояние прямой видимости при отсутствии атмосферной рефракции и при наличии нормальной атмосферной рефракции. Тоже самое выполнить, если высота передающей антенны будет h₁ = (100 +
+ N) м.
Решение:

Дано: N = 2, M = 8.

Тогда высоты h₁ = (10 + N) = (10 + 2) = 12 м,

h₂ = (10 + М) = (10 + 8) = 18 м.

Дальность прямой видимости без учета атмосферной рефракции определяется формулой [1, стр. 14]

, (3.1)

где r₀  дальность прямой видимости, км;

h₁ и h₂  высоты передающей и приемной антенн, м.



При распространении радиоволн в тропосфере происходит искривление их траекторий за счет рефракции, обусловленной изменением диэлектрической проницаемости воздуха по высоте [1, стр. 14]. При нормальной атмосферной рефракции дальность прямой видимости увеличивается и для диапазонов СВЧ, УВЧ и ОВЧ определяется формулой

, (3.2)



Если высота передающей антенны будет h₁ = (100 + N) = (100 + 2) = 102 м, то