Антенны Балагуров (1). Контрольная работа по дисциплине "Антенны и распространение радиоволн" Балагуров М. И. Группа ист11 Проверил Ищук А. А
 Скачать 2.35 Mb. Скачать 2.35 Mb.
|
|
Федеральное агентство связи Сибирский Государственный Университет Телекоммуникаций и Информатики -ширина ДН АР по нулевому излучению определена неверно! Контрольная работапо дисциплине: “Антенны и распространение радиоволн”Выполнил: Балагуров М.И. Группа: ИСТ-11 Проверил: Ищук А.А. Новосибирск, 2022 на тему: "Антенно-фидерные устройства"Задача № 1 Линейная антенная решетка состоит из n (табл. 1) ненаправленных (изотропных) излучателей, которые расположены на расстоянии d1/λ друг от друга. Излучатели питаются синфазными токами одинаковой амплитуды. Необходимо вычислить: а) ширину диаграммы направленности по половинной мощности 2φ0,5 и по направлениям нулевого излучения 2φ0 (в плоскости расположения излучателей); б) направления, в которых отсутствует излучение в пределах 1-го квадранта (φ0 ≤ 90); в) направление максимумов боковых лепестков в пределах 1-го квадранта (φmax ≤ 90); г) значения нормированной характеристики направленности главного лепестка под углами φ = 0, 2, 4, 6, 8, 10; д) рассчитать относительную интенсивность боковых лепестков диаграммы направленности в пределах 1-го квадранта (φ ≤ 90); е) величину несинфазности токов возбуждения ψ, необходимую для того, чтобы угол максимального излучения был равен φ1; ж) коэффициент направленного действия. Нарисовать антенную решетку и построить в прямоугольной системе координат ориентировочную диаграмму направленности. Примечание: Отсчет углов φ производится относительно перпендикуляра к оси, вдоль которой расположены излучатели Таблица 1
а). Определим ширину диаграммы направленности по половинной мощности 2φ0,5 и по направлениям нулевого излучения 2φ0 (в плоскости расположения излучателей). Для равномерных синфазных решеток ширина диаграммы направленности (ДН) по нулям находится из общих формул [3, стр. 241]  (1.1) (1.1)При условии, что d = d1 = 0,55, получаем 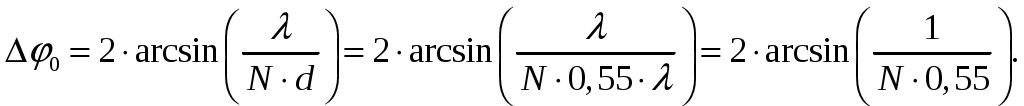 При N = n = 7, получаем 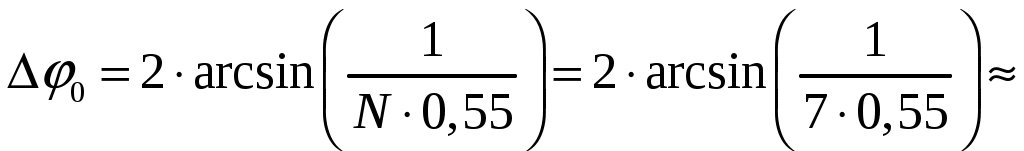 Ширина ДН на уровне 0,5 мощности находится по формуле [2, стр. 84] При условии, что d = d1 = 0,55, получаем 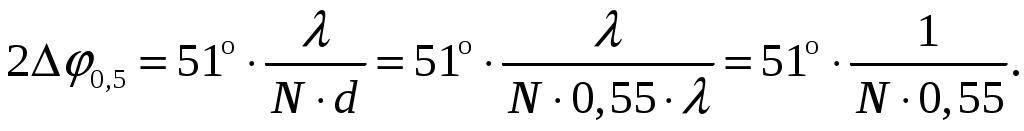 При N = n = 7, получаем 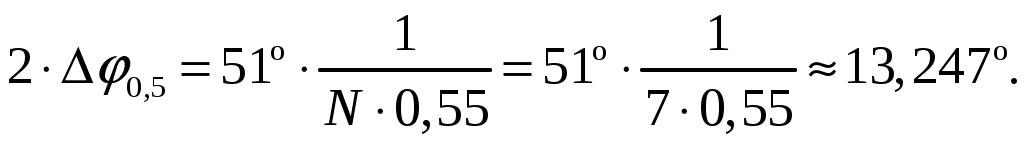 б). Определим направления, в которых отсутствует излучение в пределах 1-го квадранта (φ0 ≤ 90). Между соседними главными максимумами имеется (N - 1) нулей и, следовательно, находится (N - 2) побочных лепестков. Величины их максимумов убывают при удалении от каждого главного лепестка – наименьшими являются лепестки, расположенные в середине интервала между главными максимумами. Положения нулей определяется уравнением [2, стр. 83] где N = 7 количество излучателей; m = 1, 2, 3 и т. д. При условии, что d = d1 = 0,55 и k = 2/ получаем 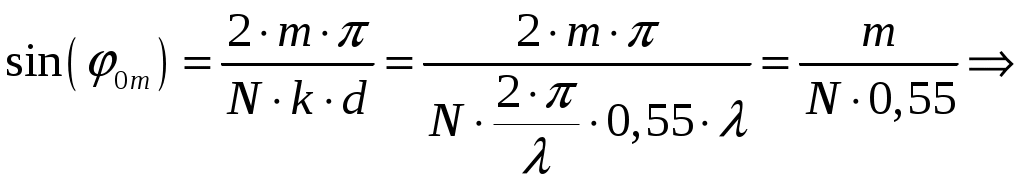  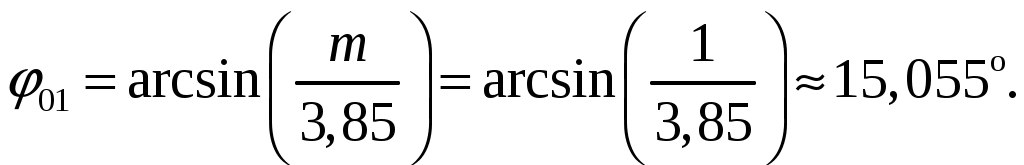 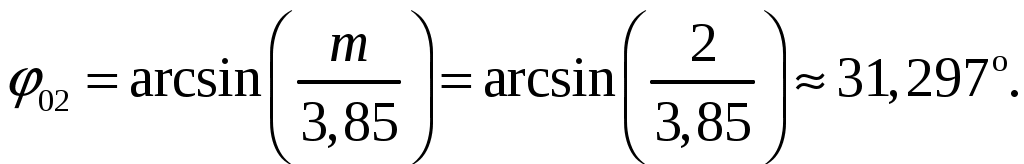 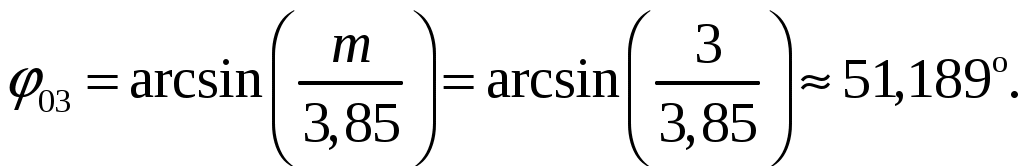 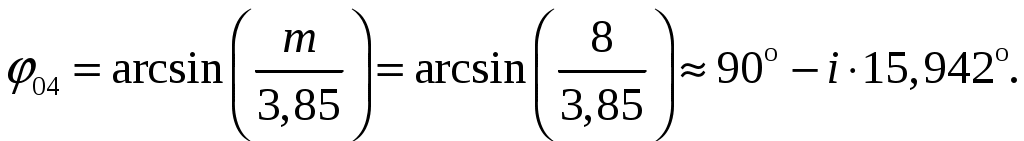 Четвертого минимума нет, так как в результатах расчета угла присутствует мнимая единица. Результаты расчетов для различных m сведем в таблицу 1.2. Таблица 1.2
в). Направление максимумов боковых лепестков в пределах 1-го квадранта (φmax ≤ 90) [2, стр. 83] 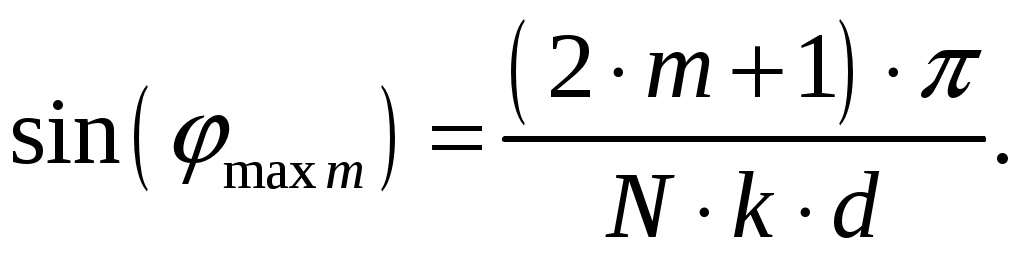 (1.4) (1.4)При условии, что d = d1 = 0,55 и k = 2/, N = n = 7 получаем 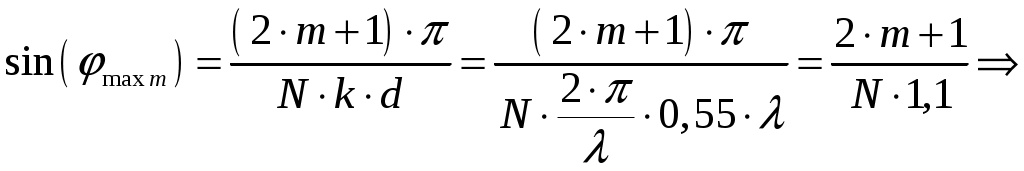 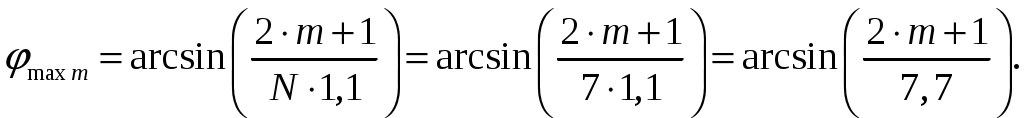 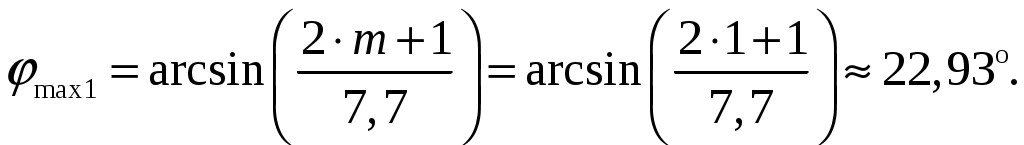 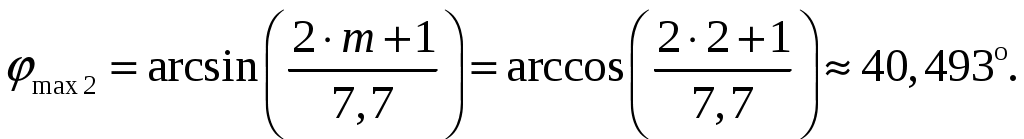 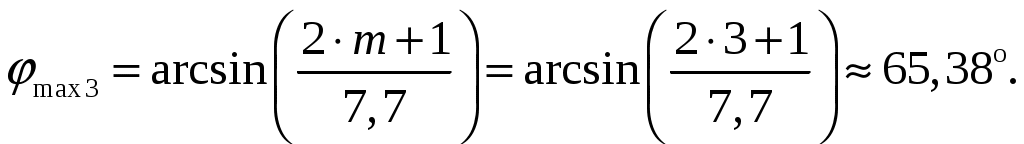 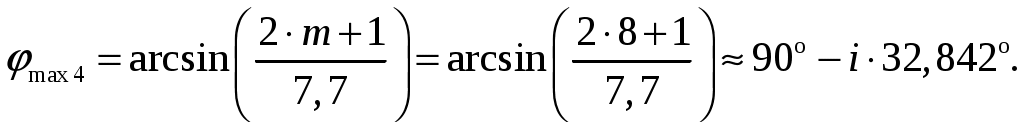 Четвертый максимум отсутствует, так как в результатах расчета угла присутствует мнимая единица Результаты расчетов для различных m сведем в таблицу 1.3. Таблица 1.3
г) Рассчитаем значения нормированной характеристики направленности главного лепестка под углами φ = 0, 2, 4, 6, 8, 10; Диаграмма направленности равномерной линейной решетки определяется соотношением [2, стр. 85] 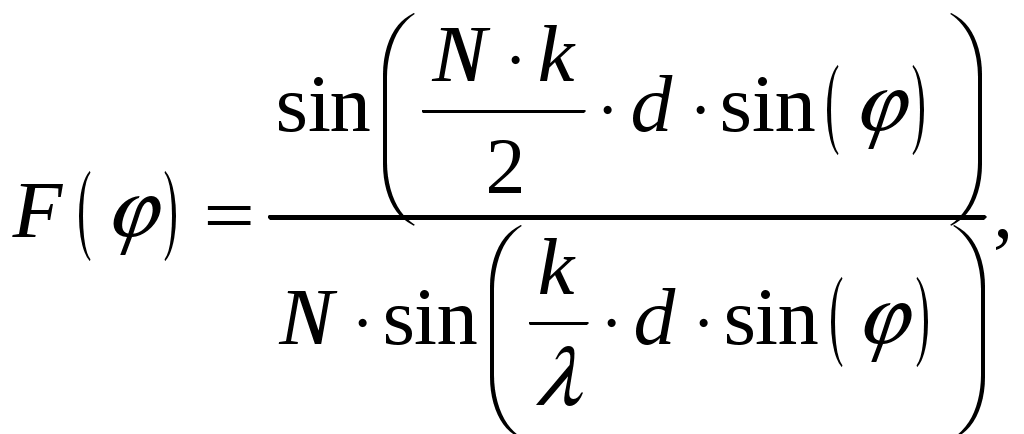 (1.5) (1.5)При условии, что d = d1 = 0,55 и k = 2/ получаем 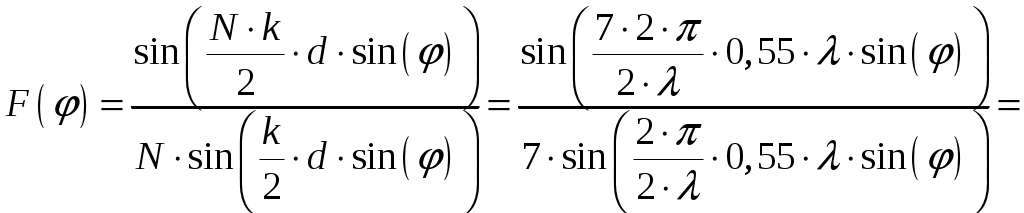 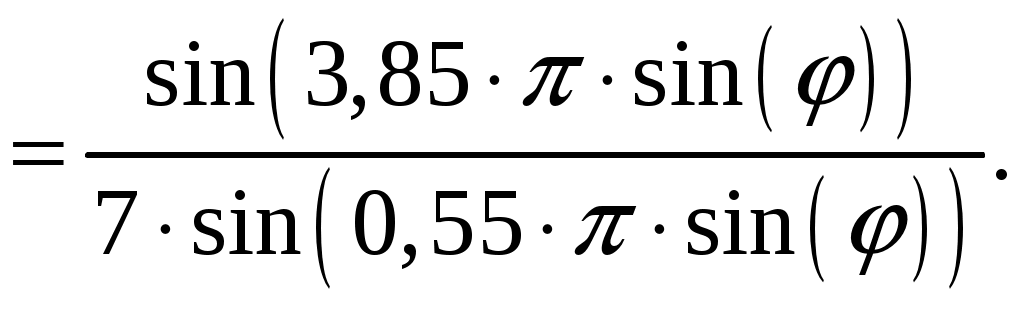 Значения отсчетов диаграммы направленности (по формуле (1.5)) рассчитанные через 2 градуса, сведены в таблицу 1.4. Таблица 1.4
1 = 0: 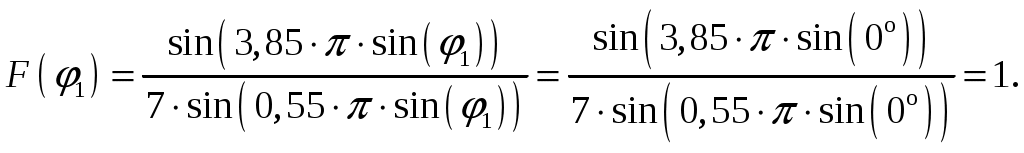 2 = 2: 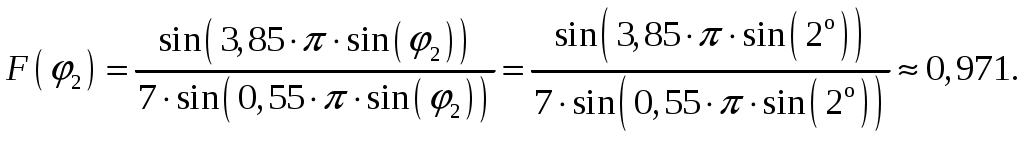 3 = 4: 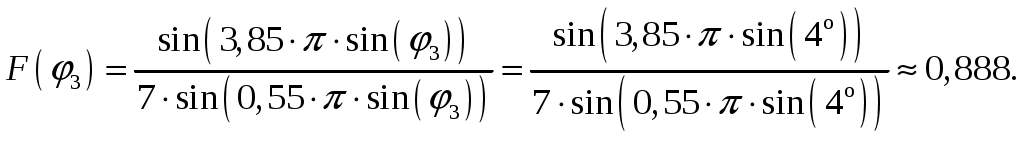 4 = 6: 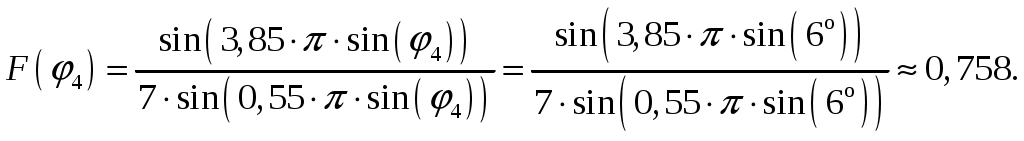 5 = 8: 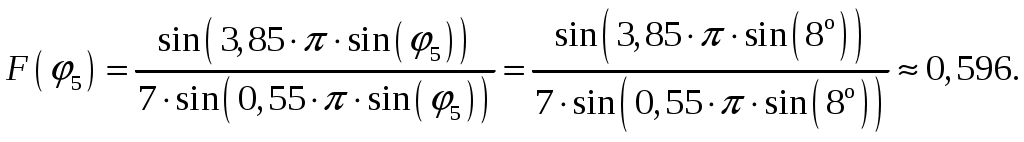 6 = 10: 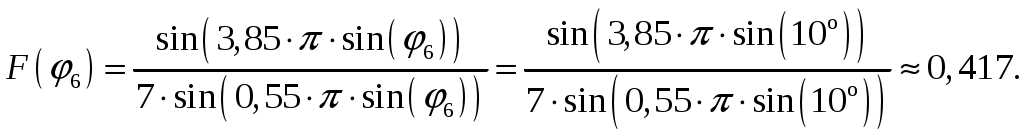 д). Относительная интенсивность боковых лепестков диаграммы направленности в пределах 1-го квадранта (φ ≤ 90) [2, стр. 84] 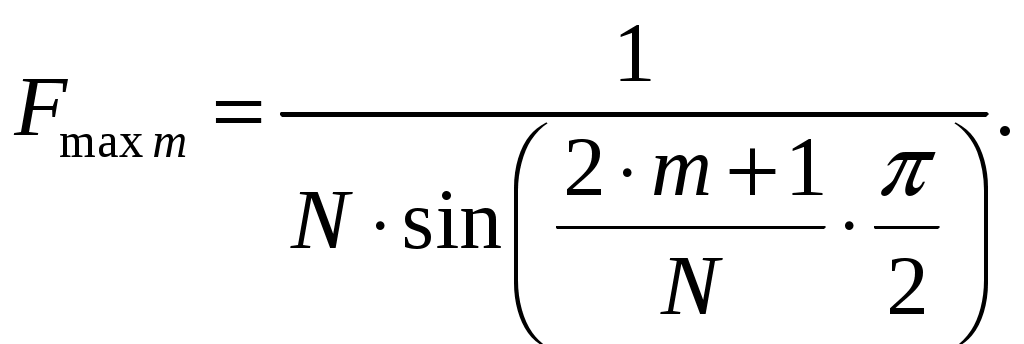 (1.6) (1.6)При условии, что N = 7 получаем 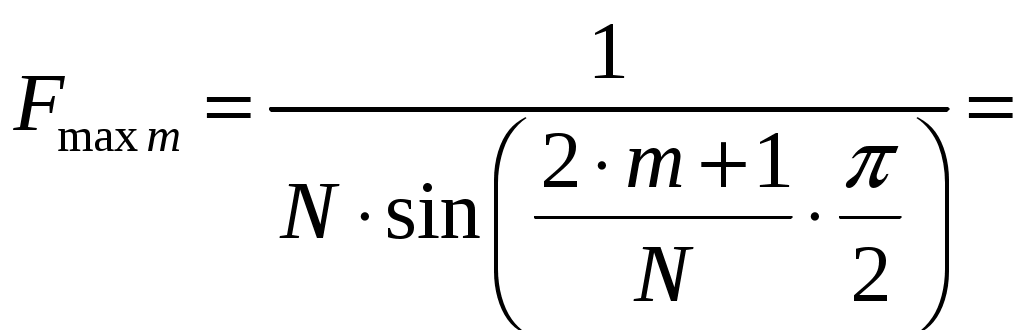 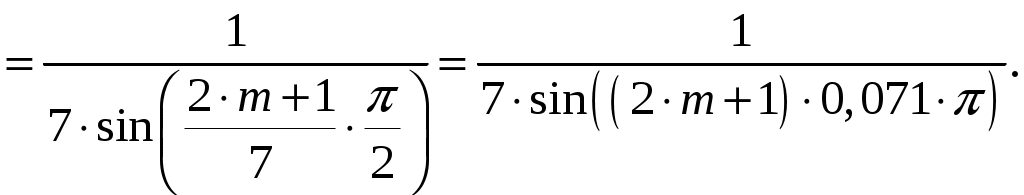 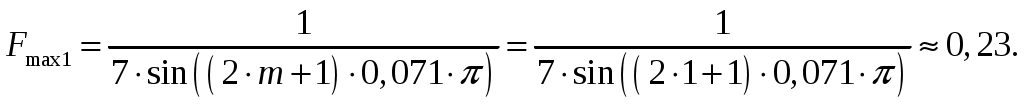 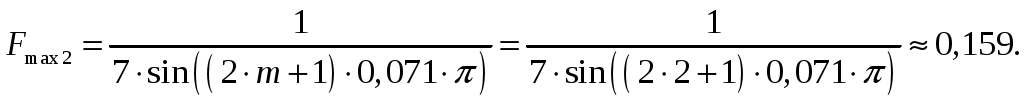 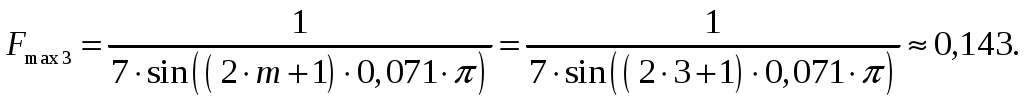 Результаты расчетов для различных m сведем в таблицу 1.5. Таблица 1.5
е). Величина несинфазности токов возбуждения ψ, необходимая для того, чтобы угол максимального излучения был равен φ1 [2, стр. 85] При условии, что d = d1 = 0,55, k = 2/ и φ1 = 25 получаем ж). Коэффициент направленного действия определяется [2, стр. 85] где L = (N 1)d длина решетки, N количество излучателей, N = 7; d расстояние между излучателями, d = d1 = 0,55. 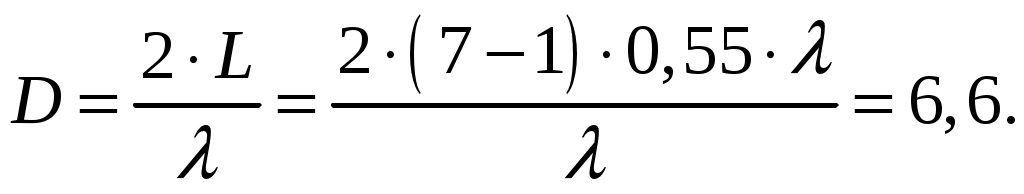 2. Нарисовать антенную решетку и построить в прямоугольной системе координат ориентировочную диаграмму направленности. Десяти элементная линейная эквидистантная антенная решетка из изотропных излучателей, расположенных на расстоянии 0,55 длины волны, приведена на рис. 1.1. = 0  = 90 ИИ1 ИИ2 ИИ3 ИИ5 ИИ6 ИИ7 ИИ4            = -90       d1 = 0,55 d2 = 0,55 d5 = 0,55 d6 = 0,55 d3 = 0,55 d4 = 0,55       Рис. 1.1. Семи элементная линейная эквидистантная антенная решетка из изотропных излучателей, расположенных на расстоянии 0,55 длины волны: ИИ – изотропный излучатель Диаграмма направленности в отсчете углов φ относительно перпендикуляра к оси, вдоль которой расположены излучатели, построенная с помощью программы MathCad приведена на рис. 1.2. 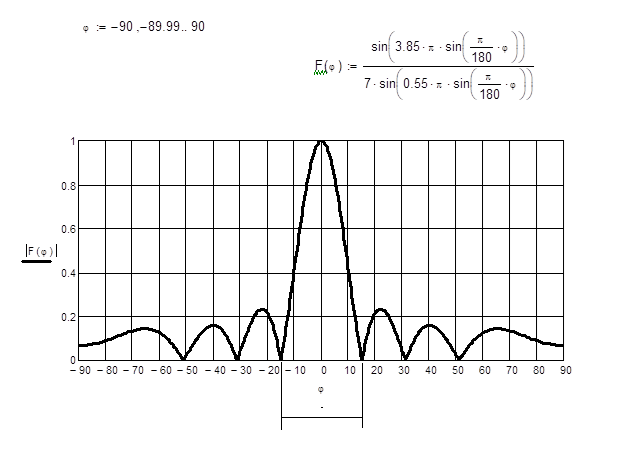 Рис. 1.2. Диаграмма направленности линейной антенной решетки Рис. 1.2. Диаграмма направленности линейной антенной решетки из 7 ненаправленных (изотропных) излучателей, которые расположены на расстоянии 0,55 и питаются синфазными токами одинаковой амплитуды Из диаграммы видно, что ширина главного лепестка по нулевому излучению составляет 0 = 2*16=32 град. Задача № 2б Антенна в виде параболоида вращения имеет угол раскрыва 0 (табл. 2.1) и коэффициент направленного действия Д (табл. 2.1) при длине волны и коэффициенте использования поверхности = 0,5. 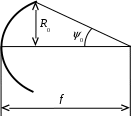 Рис. 2.1 Необходимо определить: а) радиус раскрыва антенны R0; б) фокусное расстояние f; в) объяснить почему коэффициент использования поверхности < 1. Таблица 2.1 Исходные данные для задачи
Для параболида вращения фокусное расстояние f, радиус раскрыва R0 и угол раскрыва зеркала 0 связаны уравнениями [1, стр. 90] 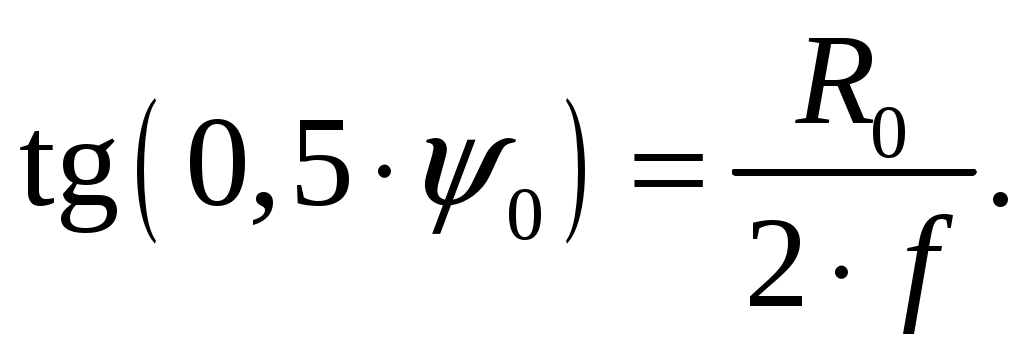 (2.1) (2.1)Коэффициент направленного действия поверхностных антенн [1, стр. 89] где S = R02 поверхность раскрыва, м2; коэффициент использования поверхности, = 0,5. Коэффициент направленного действия (2.2) с учетом полученного соотношения для S, примет вид 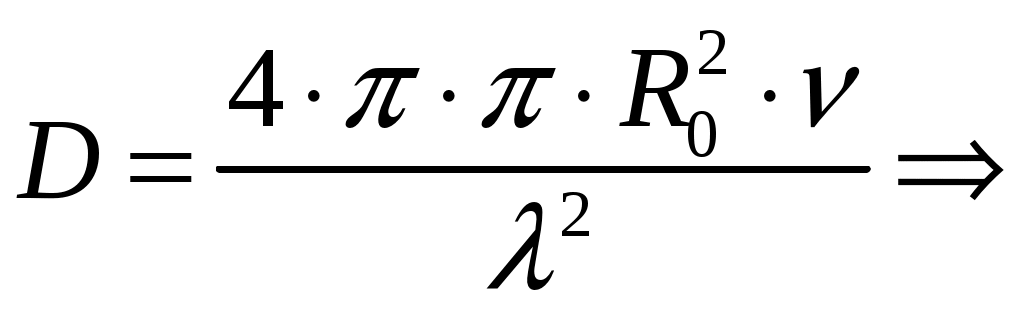 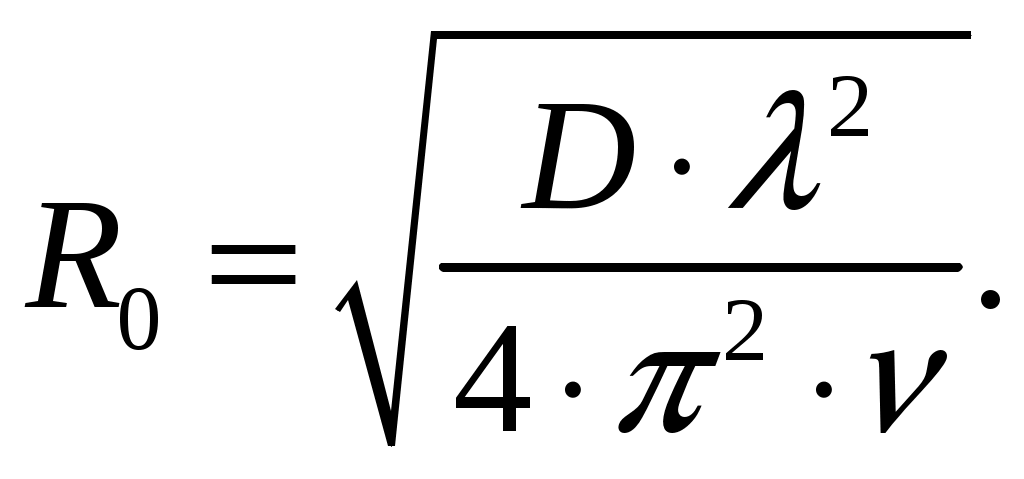 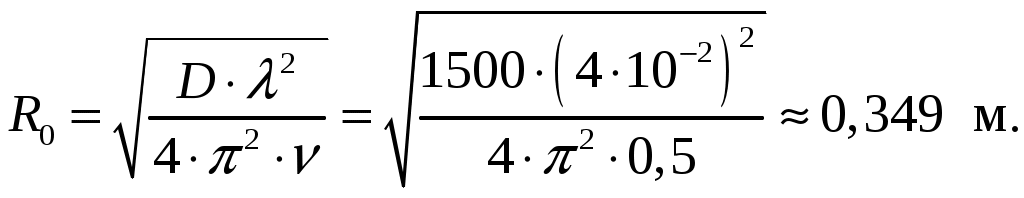 Согласно формуле (2.1) рассчитываем фокусное расстояние Таким образом, получено: R0 = 0,349 м; f = 0,479 м. Проверку выполним, рассчитав коэффициент направленного действия: 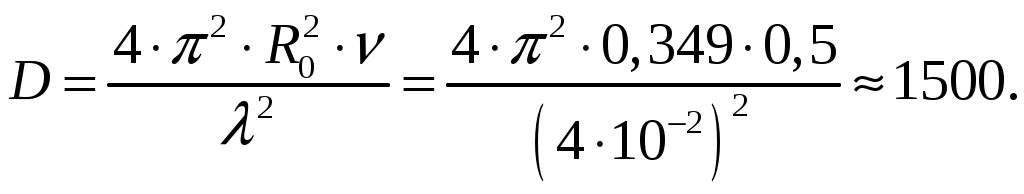 По результатам проверки видно, что D = 1500 = Д = 1500. Объясним, почему коэффициент использования поверхности параболических антенн < 1. Коэффициент направленного действия зеркальной антенны D можно рассчитать по формуле (2.2), заменив в ней апертурный КИП множителем РЕЗ (результирующий или полный КИП), учитывающим уменьшение КНД из-за действия ряда факторов. К этим факторам относятся: переливание части излученной облучателем энергии через края зеркала, вызывающее увеличение уровня боковых лепестков ДН зеркальной антенны в задних квадрантах (дальние боковые лепестки); ошибки в фазовом распределении на раскрыве; затенение части поверхности раскрыва облучателем и элементами его крепления; кросс-поляризация излучаемого поля и др. [2, стр. 176] Таким образом, где Здесь a апертурный КИП раскрыва зеркала, определяемый амплитудным распределением в синфазном раскрыве; 1, 2, 3 и т. д. множители, определяемые перечисленными факторами. Остановимся подробнее на влиянии множителя 1 на КНД антенны. Полагая для простоты, что все остальные множители (2, 3 и т. д.) равны единице, получим Множитель 1 коэффициент перехвата есть отношение мощности, излученной зеркалом Р, к мощности, излученной облучателем РОБЛ (потери в зеркале здесь не учитываются). Следовательно, при осесимметричной ДН облучателя 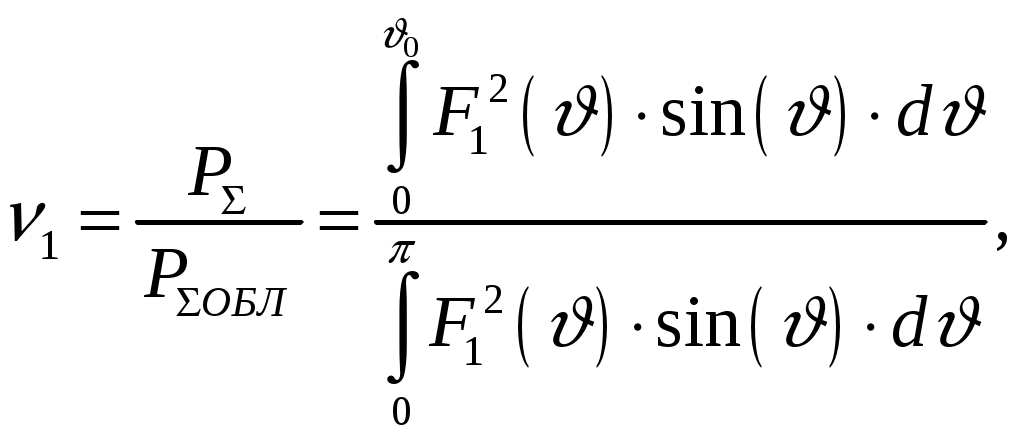 (2.5) (2.5)где F1() нормированная характеристика направленности облучателя. Иногда пользуются понятием коэффициента рассеяния зеркальной антенны 1 = l 1, определяемого долей мощности поля, проходящей мимо зеркала, т. е. приходящейся на область дальних, боковых и задних лепестков антенны. Полный коэффициент рассеяния показывает относительную долю мощности излучения антенны (Рбок/Робл), приходящуюся на область всех боковых (ближних, дальних и задних) лепестков ДН антенны. Коэффициент усиления зеркальной антенны G = D, где = Р/Робл; Робл мощность, подведенная к облучателю. Коэффициент полезного действия зеркальной антенны учитывает тепловые потери энергии в облучателе, в элементах крепления облучателя, в краске, покрывающей внутреннюю поверхность зеркала, и т. д. Обычно = 0,9 1. Апертурный КИП a = Sд/S зеркальной антенны, если амплитудное распределение не зависит от . Если в качестве облучателя используется рупор, то коэффициент перехвата 1 можно определить по приближенной формуле 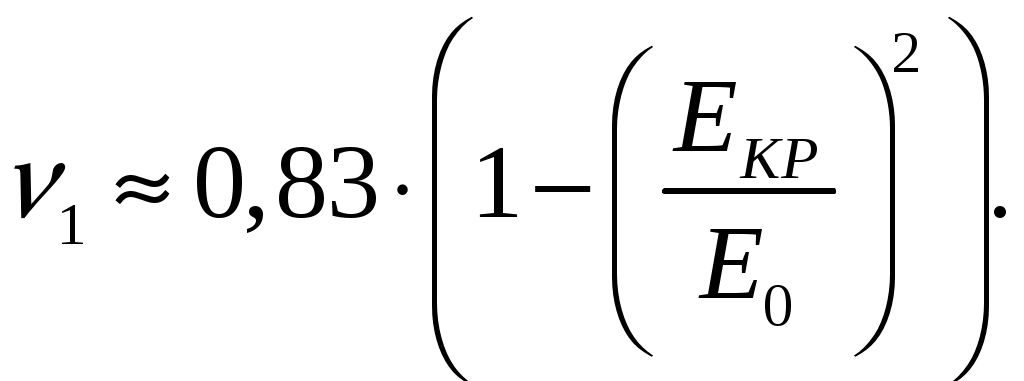 (2.6) (2.6)Если пространственная ДН облучателя представляет тело вращения относительно оси зеркала z, то КНД антенны с учетом множителя перехвата можно вычислить по формуле 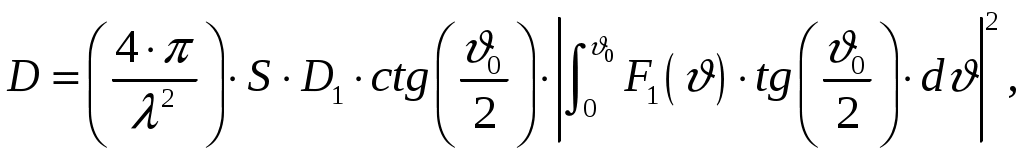 (2.7) (2.7)где D1 КНД облучателя в главном направлении. Величины a и 1 определяются формой ДН облучателя и величиной отношения R0/f. Множитель 2, учитывающий влияние затенения на КНД антенны, может быть записан в виде 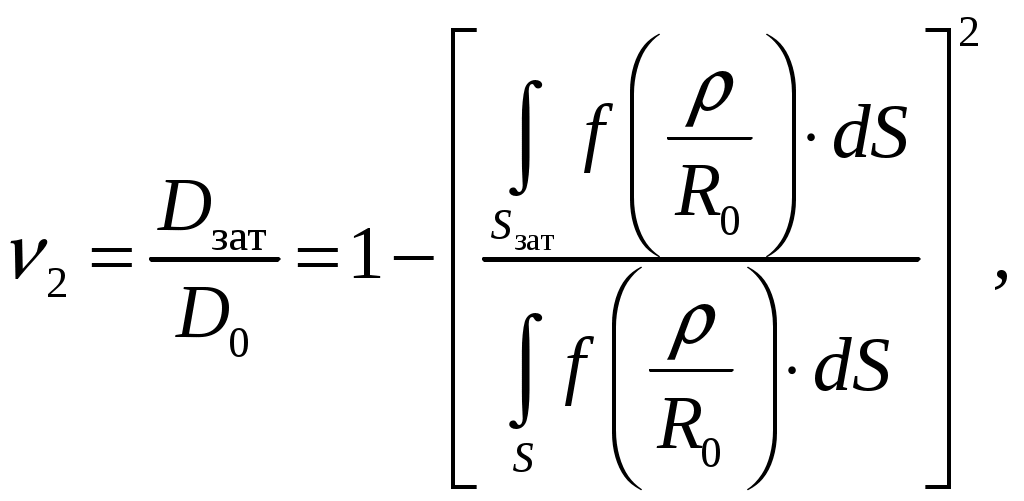 (2.8) (2.8)где Dзат КНД антенны с учетом затенения; D0 КНД без затенения; Sзат затененная часть раскрыва зеркала. Если 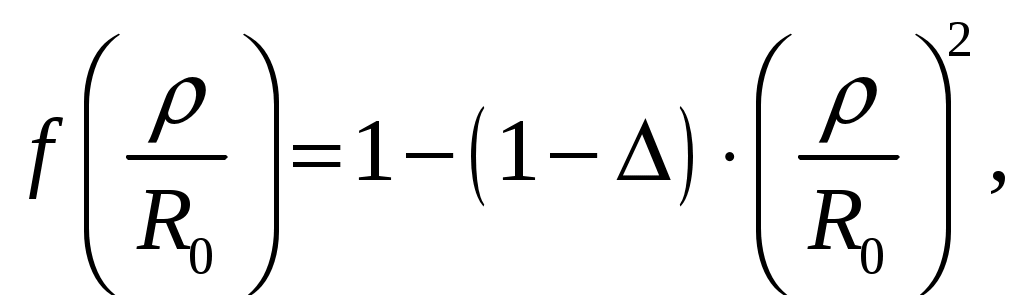 то то 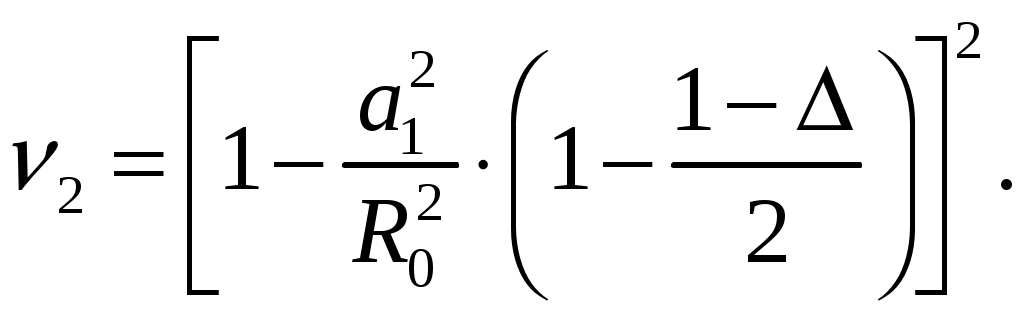 При 0,3 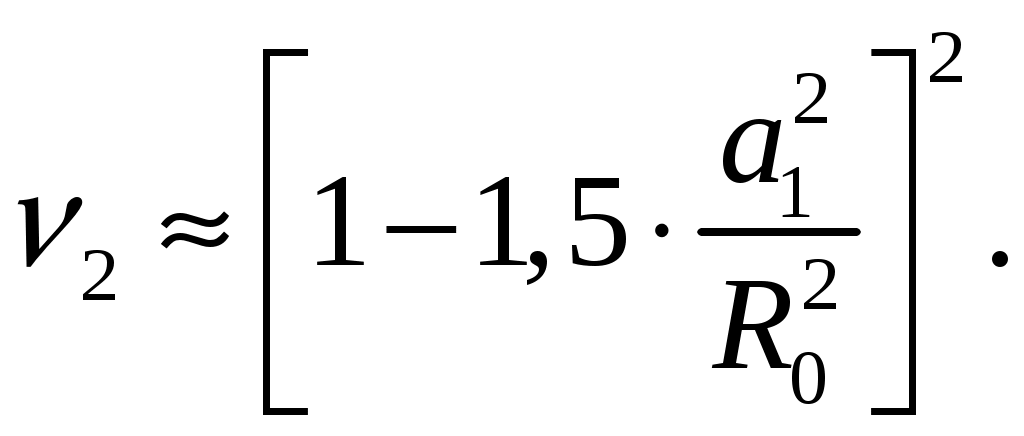 С точки зрения получения максимального КНД при заданных размерах зеркала идеальной является ДН облучателя, изображенная на рис. 2.2, кривая 2. Эта ДН является осесимметричной и имеет два главных максимума, соответствующих краям зеркала. При этом амплитудное распределение раскрыва зеркала получается равномерным (с учетом разных расстояний от фокуса зеркала до его вершины), т. е. a = 1; переливание энергии за края зеркала отсутствует (ДН имеет бесконечную крутизну спада); 1 = 1( = 0). 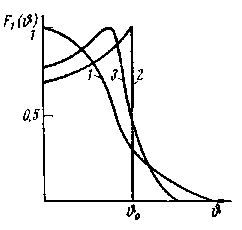 Рис. 2.2 Диаграммой направленности, похожей на кривую 1 рис. 2.2, обладают такие облучатели, как симметричный вибратор с рефлектором, рупор, щелевой излучатель. В интервале углов 0 /2 эти ДН довольно хорошо аппроксимируются функцией вида cosn(). Они весьма далеки от идеальной (см. рис. 2.2, кривая 2). Если при заданной форме зеркала (R0/f = const) расширять ДН облучателя, то амплитудное распределение в раскрыве зеркала становится более равномерным (a растет). Однако вместе с тем увеличивается доля энергии, проходящей мимо зеркала (уменьшается 1). При сужении ДН облучателя, наоборот, уменьшается a и увеличивается 1. Два противоположно действующие на результирующий КИП и КНД фактора при постоянной величине R0/f или угле раскрыва зеркала 20 и измеряемой ширине ДН облучателя определяют условие оптимального облучения зеркала с точки зрения получения максимального КНД. Это условие примерно выполняется, если ДН облучателя обеспечивает (с учетом разных расстояний от фокуса зеркала до его вершины и краев) выполнение соотношения 20lg(Eкр/E0) = 10 дБ, или Eкр/E0 = 0,316, где Екр напряженность поля на краю зеркала. Однако при этом результирующий КИП антенны оказывается все же небольшим (обычно 0,45 0,55). Кроме того, переливание энергии через края зеркала, приводящее к росту уровня дальних боковых и задних лепестков ДН антенны, значительно. Поэтому для снижения их уровня часто приходится уменьшать облучение краев зеркала, что еще больше снижает результирующий КИП. Поэтому облучатели указанных типов в настоящее время применяются только в тех случаях, когда величина результирующего КИП не играет большой роли (обычно в случае малых параболических антенн). Ясно, что с точки зрения электромагнитной совместимости применение облучателей с ДН, описываемой функцией cosn(), нежелательно. Параболические антенны, применяемые для космической радиосвязи и в радиоастрономии, должны иметь высокий КНД (обычно больше, чем 105), чтобы обеспечить прием весьма слабых сигналов; диаметры раскрывов этих антенн достигают десятков метров. Стоимость изготовления больших зеркал растет при увеличении диаметра раскрыва примерно пропорционально второй степени диаметра и даже быстрее. Поэтому результирующий КИП таких антенн, характеризующий степень использования габаритных размеров антенны, должен быть велик. Шумовая температура антенны, определяемая в основном уровнем дальних боковых лепестков ДН, должна быть низкой. Для обеспечения высокого рез и низкой ТА ДН облучателя должна иметь форму, по возможности приближающуюся к идеальной. Она должна быть осесимметричной, иметь достаточно равномерное распределение мощности в области главного лепестка, соответствующей углу раскрыва зеркала, и обладать крутыми спадами (рис. 2.2, кривая 3). Похожие ДН можно получить с помощью рупоров с несинфазными раскрывами (расфазированные рупоры), антенн бегущей волны, работающих в режиме c/ < 1, и некоторых других специальных видов облучателей. Так, например, в двухзеркальной антенне системы «Орбита» применен облучатель в виде двухзаходной логарифмической спирали. С помощью таких облучателей путем оптимизации их ДН и геометрических параметров зеркала можно обеспечить высокий a при 1 = 0,954 0,97 (при обычном облучателе 1 = 0,8 0,85) и получать рез на 15 20 % выше, чем у обычной зеркальной антенны, т. е. рез = 0,7 0,75. Шумовая температура антенны может быть снижена до 10 15 К. Такие антенны обладают хорошей ЭМС. Параболоиды вращения можно изготавливать очень больших относительных размеров и получать весьма узкие ДН (угловые минуты) и КНД порядка миллионов единиц. Такие параболоиды применяются в радиоастрономии и для космической радиосвязи. Например, параболоид физического института им. П. Н. Лебедева имеет R0 = 11 м, = 8 мм. Антенна радиотелескопа института им. Планка (ФРГ, Эффельберг) имеет R0 = 50 м при длине волны до 1 см, массу 3200 т, отклонение поверхности от расчетной 1 мм. Список литературы 1. Чернышов, В. П. Распространение радиоволн и антенно-фидерные устройства. Задачи и упражнения. – М.: Радио и связь, 1982. – 144 с.: ил. 2. Кочержевский, Г. Н. Антенно-фидерные устройства: Учебник для вузов. – 3-е изд., доп. и перераб. – М.: Радио и связь, 1981. – 280 с., ил. 3. Жук, М. С. Проектирование антенно-фидерных устройств / М. С. Жук, Ю. Б. Молочков. – М.-Л.: Энергия, 1966. 648 с.: илл. на тему “Распространение радиоволн» Исходные данные для решения задач
|
