информатика. Контрольная XV_pycharm. Контрольная работа по дисциплине Численные методы
 Скачать 52.67 Kb. Скачать 52.67 Kb.
|
|
Контрольная работа по дисциплине «Численные методы» Срок сдачи 26.12.2022 Все задания реализуются на языке программирования Python. Примеры заданий брать из соответствующих домашних заданий, свой вариант. # Задание 1. Решение СЛАУ (систем линейных алгебраических уравнений) методом Гаусса.Код программы import numpy as np import sys # Число переменных n = 4 # Создаем numpy array размерностью n*n+1 и заполняем нулями a = np.zeros((n,n+1)) # Создаем numpy вектор размерностью n и заполняем нулями x = np.zeros(n) # Исходная матрица системы a = np.array([[1,1,1,0,1], [1,2,2,1,0], [2,3,4,2,0], [3,4,5,3,0]]) # Гауссово исключение for i in range(n): if a[i][i] == 0.0: sys.exit('Деление на ноль!') for j in range(i+1, n): ratio = a[j][i]/a[i][i] for k in range(n+1): a[j][k] = a[j][k] - ratio * a[i][k] # Обратный ход x[n-1] = a[n-1][n]/a[n-1][n-1] for i in range(n-2,-1,-1): x[i] = a[i][n] for j in range(i+1,n): x[i] = x[i] - a[i][j]*x[j] x[i] = x[i]/a[i][i] print('\nРешение системы: ') for i in range(n): print('X%d = %0.2f' %(i,x[i]), end = '\t') discrepancy=np.matmul(a[:,:4], x.T) - a[:,4] print('\nНевязка: ') print(discrepancy) 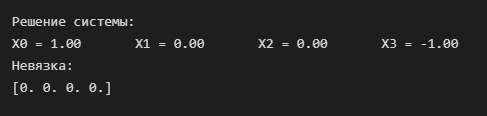 # Задание 2. Решение нелинейных уравнений (метод деления отрезка пополам, метод Ньютона, метод простой итерации). Реализовать методы решения уравнений и сравнить по двум параметрам: 1. сложность алгоритма 2. длительность решения Локализуем корни, строим график функции Код программы import matplotlib.pyplot as plt import numpy as np # Построим график, с целью отделения корней fig, ax = plt.subplots() ax.set_title('График функции x^3+2x+4') ax.set_xlabel('x') ax.set_ylabel('y') x = np.linspace(-2, 2, 100) # X от -2 до 2 y = x**3+2*x+4 plt.grid(True) ax.plot(x, y) plt.show() 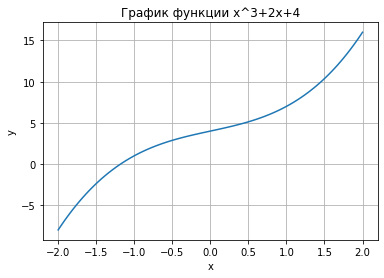 # Интервал изоляции корня [-1.5;-1] # метод деления отрезка пополамКод программы import time import math my_func = lambda x: x ** 3 + 2 * x + 4 def half_divide(a, b, eps, f): x = (a + b) / 2 i=0 while math.fabs(f(x)) >= eps: x = (a + b) / 2 a, b = (a, x) if f(a) * f(x) < 0 else (x, b) i=i+1 return (a + b) / 2, i a, b = -1.5, -1.0 eps = 0.0001 tic = time.perf_counter() print('Корень = %0.4f Число итераций = %d' % half_divide(a, b, eps, my_func)) toc = time.perf_counter() print(f"Вычисление заняло {toc - tic:0.6f} секунд")  # метод НьютонаКод программы import time import math my_func = lambda x: x ** 3 + 2 * x + 4 dif_func = lambda x: 3*x*x+2 def newtons(a, b, eps,f, f1): x0 = (a + b) / 2 x1 = x0 - (f(x0) / f1(x0)) i=0 while True: if math.fabs(x1 - x0) < eps: return x1,i x0 = x1 x1 = x0 - (f(x0) / f1(x0)) i=i+1 a, b = -1.5, -1.0 eps = 0.0001 tic = time.perf_counter() print ('Корень = %0.4f Число итераций = %d' % newtons(a, b, eps, my_func, dif_func)) toc = time.perf_counter() print(f"Вычисление заняло {toc - tic:0.6f} секунд") # метод простой итерации# Представим уравнение в форме: # x = x - λ(x3+2*x+4) # Найдем максимальное значение производной от функции f(x) = x3+2*x+4 Код программы my_func = lambda x: x ** 3 + 2 * x + 4 dif_func = lambda x: 3*x*x+2 a, b = -1.5, -1.0 eps = 0.0001 q = max([abs(dif_func(x)) for x in np.arange(a, b, eps)]) print(q) lam=1/q print(lam) 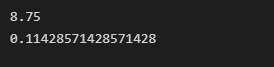 # Таким образом решаем уравнение x = x - lam*(x3+2*x+4) Код программы import time import math def simple_iteration(a,b,eps,f): x_prev = (a + b) / 2 x_cur = f(x_prev) iters = 0 while abs(x_cur - x_prev) >= eps: x_prev = x_cur x_cur = f(x_prev) iters += 1 return x_cur, iters my_func = lambda x: x-0.11428571*(x ** 3 + 2 * x + 4) a, b = -1.5, -1.0 eps = 0.0001 tic = time.perf_counter() print ('Корень = %0.4f Число итераций = %d' % simple_iteration(a, b, eps, my_func)) toc = time.perf_counter() print(f"Вычисление заняло {toc - tic:0.6f} секунд") # Задание 3. Реализовать алгоритм метода Симпсона.Код программы #import numpy as np def f(x): return 7+x-2*x*x def simpson(x0,xn,n): h = (xn - x0) / n sum = f(x0) + f(xn) for i in range(1,n): k = x0 + i*h if i%2 == 0: sum = sum + 2 * f(k) else: sum = sum + 4 * f(k) sum = sum * h / 3 return sum I_simp=simpson(1.0, 4.0, 6) #Точное значение интеграла = -27/2 err_simp = -27/2 - I_simp print('Искомый интеграл = ',I_simp) print('Абсолютная ошибка = ',abs(err_simp)) |
