|
|
Детали машин. детали машин. Контрольная работа по дисциплине Детали машин
Тамбовское областное государственное бюджетное
профессиональное образовательное учреждение
«Котовский индустриальный техникум»
Контрольная работа
по дисциплине «Детали машин»
Вариант № 6
Выполнил:
Студент курса 2 заочного отделения
Группа 1 НПО
специальность 15.02.01 «Монтаж и
эксплуатация промышленного оборудования»
Карачун А.И.
___________
подпись студента
Проверил преподаватель:
Кочетков В.В.
Оценка _________
___________
подпись преподавателя
Котовск
Содержание
Вопрос 1…………………………………………………………. 3
Вопрос 2 ………………………………………………………… 6
Список литературы …………………………………………….. 20
Вопрос № 1 Геометрические параметры метрической резьбы.
Метрическая резьба – это винтовая нарезка на наружных или внутренних поверхностях изделий. Форма выступов и впадин, которые ее формируют, представляет собой равнобедренный треугольник. Метрической эту резьбу называют потому, что все ее геометрические параметры измеряются в миллиметрах. Она может наноситься на поверхности как цилиндрической, так и конической формы и использоваться для изготовления крепежных элементов различного назначения. Кроме того, в зависимости от направления подъема витков резьба метрического типа бывает правая или левая. Помимо метрической, как известно, есть и другие типы резьбы – дюймовая, питчевая и др. Отдельную категорию составляет модульная резьба, которую используют для изготовления элементов червячных передач.
Основные параметры и сферы применения
Наиболее распространенной является метрическая резьба, наносимая на наружные и внутренние поверхности цилиндрической формы. Именно она чаще всего используется при изготовлении крепежных элементов различного типа:
- анкерных и обычных болтов;
- гаек;
- шпилек;
- винтов и др.
Детали конической формы, на поверхность которых нанесена резьба метрического типа, требуются в тех случаях, когда создаваемому соединению необходимо придать высокую герметичность. Профиль метрической резьбы, нанесенной на конические поверхности, позволяет формировать плотные соединения даже без использования дополнительных уплотнительных элементов. Именно поэтому она успешно применяется при монтаже трубопроводов, по которым транспортируются различные среды, а также при изготовлении пробок для емкостей, содержащих жидкие и газообразные вещества. Следует иметь в виду, что профиль резьбы метрического типа один и тот же на цилиндрических и на конических поверхностях.
Виды резьб, относящихся к метрическому типу, выделяют по ряду параметров, к которым относятся:
- размеры (диаметр и шаг резьбы);
- направление подъема витков (левая или правая резьба);
- расположение на изделии (внутренняя или наружная резьба).
Геометрические параметры
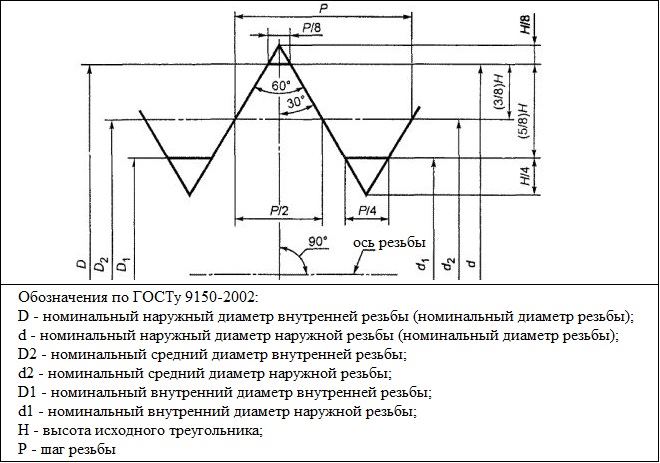
Рассмотрим геометрические параметры, которые характеризуют основные элементы резьбы метрического типа.
Номинальный диаметр резьбы обозначается буквами D и d. При этом под буквой D понимают номинальный диаметр наружной резьбы, а под буквой d – аналогичный параметр внутренней.
Средний диаметр резьбы в зависимости от ее наружного или внутреннего расположения обозначается буквами D2 и d2.
Внутренний диаметр резьбы в зависимости от ее наружного или внутреннего расположения имеет обозначения D1 и d1.
Внутренний диаметр болта используется для расчета напряжений, создаваемых в структуре такого крепежного изделия.
Шаг резьбы характеризует расстояние между вершинами или впадинами соседних резьбовых витков. Для резьбового элемента одного и того же диаметра различают основной шаг, а также шаг резьбы с уменьшенными геометрическими параметрами. Для обозначения этой важной характеристики используют букву P.
Ход резьбы представляет собой расстояние между вершинами или впадинами соседних витков, сформированных одной винтовой поверхностью. Ход резьбы, которая создана одной винтовой поверхностью (однозаходная), равен ее шагу. Кроме того, значение, которому соответствует ход резьбы, характеризует величину линейного перемещения резьбового элемента, совершаемого им за один оборот.
Такой параметр, как высота треугольника, который формирует профиль резьбовых элементов, обозначается буквой H.
Вопрос №2 Геометрический расчет червячного колеса ЧП. Материалы венцов червячных колес и методы изготовления ЧК.
К основным геометрическим параметрам червячных передач с цилиндрическим червяком относятся рабочее межосевое расстояние aw, номинальное передаточное число Whom, коэффициент делительного диаметра червяка q и модуль передачи т.
В настоящее время рекомендуемые значения этих параметров устанавливаются двумя стандартами:
ГОСТ 2144-76 Передачи червячные цилиндрические. Основные параметры. Данный стандарт распространяется на ортогональные цилиндрические червячные передачи для редукторов, в том числе и комбинированных. Стандарт устанавливает перечень предпочтительных значений номинальных передаточных чисел wH0M и перечень межосевых расстояний aw.
ГОСТ 19672-74 Передачи червячные цилиндрические. Модули и коэффициенты диаметра червяка. Стандарт устанавливает список рекомендуемых к применению модулей в осевом сечении тх и перечень коэффициентов диаметра червяка q.
Соотношения параметров витка червяка и зуба колеса определяет ГОСТ 19036-94 Передачи червячные цилиндрические. Исходный червяк и исходный производящий червяк. Данный стандарт распространяется на все основные виды ортогональных цилиндрических червячных передач, таких как ZA, ZI, ZN, ZK, ZT и устанавливает параметры исходного червяка и исходного производящего червяка (червячной фрезы), а также радиальные зазоры в червячных передачах с модулем т от 1 до 25 мм.
В дальнейшем нами будут рассматриваться только червяки типов ZA и ZI. Для этих червяков стандарт устанавливает основные параметры витков, боковые и радиальные зазоры, радиусы кривизны переходной кривой. В червячных передачах с архимедовым червяком устанавливается делительный угол профиля витка в осевом сечении ах равным 20°. Для эвольвентных червяков стандартизирован угол профиля витка ап в нормальном сечении на делительном цилиндре, который также равен 20°.
Все линейные размеры профиля витка червяка даются в виде коэффициентов, т.е. в долях модуля т. При этом для архимедовых червяков в большинстве дальнейших расчетов используется осевой модуль тх, а для эвольвентных чаще используется нормальный модуль тп.
К основным параметрам витка относятся:
- коэффициент высоты головки витка червяка ha *= 1;
- радиальные зазоры на червяке и червячном колесе с = Сг =0.2;
- коэффициент высоты ножки витка червяка /?п = 1 + С ;
- коэффициент полной высоты витка h*= 2 + с*.
Коэффициент расчетной толщины витка s* для архимедовых червячных передач равен 0.5л:, для эвольвентных 0.45л:. В обоснованных случаях для обоих типов передач допускается изменение коэффициента .v в пределах (0.4-0.5)л:.
Для червячных передач с модулем 0.1<т<1 разработан отдельный ГОСТ 20184-81 Передачи червячные цилиндрические мелкомодульные. Исходный червяк и исходный производящий червяк. Углы профиля ах для архимедовых и ап для эвольвентных червяков, а также большая часть параметров витка, аналогичны параметрам, указанным в ГОСТ 19036-94. Исключением являются коэффициент высоты головки витка червяка ha , который может быть равен как 1, так и 1.1, и коэффициент радиального зазора с , задаваемый в пределах от 0.25 до 0.4. Коэффициент расчетной толщины витка червяка .v с червяками ZA и Z1 равен 0.5л:.
Методы расчета геометрических параметров червячной передачи с цилиндрическим червяком и межосевым углом, равным 90°, а также геометрических и зубоизмерительных параметров червяков устанавливает ГОСТ 19650-97 Передачи червячные цилиндрические. Расчёт геометрических параметров.
К исходным данным необходимым для выполнения расчета червячной передачи относятся: параметры исходного червяка по ГОСТ 19036-94; вид червяка; модуль т; коэффициент делительного диаметра червяка q межосевое расстояние aw и передаточное число u=z2lz, которые желательно выбрать в соответствии с рекомендациями, указанными в ГОСТ 2144-76.
В ряде случаев, особенно при проектировании силовых передач, набор заданных конструктору данных может состоять лишь из передаточного числа и, числа оборотов червяка п и крутящего момента на колесе Т2 либо мощности электродвигателя Nd. При таком наборе исходных данных предварительное значение рабочего межосевого расстояния можно рассчитать по формуле:

Указанная формула позволяет ориентировочно оценить габариты проектируемой передачи. Значение рабочего межосевого расстояния, рассчитанное по формуле (2.2.1), является приближенным и не учитывает многие факторы, влияющие на нагрузочную способность, а, следовательно, и на габариты самой передачи. Поэтому в ходе выполнения проверочного прочностного расчета полученное межосевое расстояние может быть скорректировано на некоторую величину, как правило, не превышающую 5-10% от первоначального значения aw. С целью унификации расчетное межосевое расстояние может быть округлено в большую сторону до ближайшего из предложенных в ГОСТ 2144- 76. Факторы, влияющие на нагрузочную способность червячной передачи, и расчет её оценки подробно рассмотрены в разделе 2.5.
Далее, исходя из заданного передаточного отношения и, следует назначить число заходов червяка z, и число зубьев колеса z2, если они не были изначально заданы в исходных данных. Число зубьев колеса z2=u-z нужно принимать в пределах 25... 100.
Из сказанного следует, что для передаточных чисел в диапазоне от 40 до 100, оптимальным является червяк с одним заходом. При передаточных числах w=25...40 допускается использовать как одно-, так и двухзаходные червяки, отдавая предпочтение двухзаходным при и<30. В червячных передачах с w=12,5...25 следует применять двухзаходные червяки. Червяки с четырьмя заходами рекомендуется использовать для передаточных чисел в интервале t/=7...12,5. Трехзаходные червяки ГОСТ 2144-76 не рекомендует применять, но для передаточных отношений в интервале п=10...25 их применение может оказаться целесообразным.
В делительных и настроечных механизмах некоторых станков и в ряде других случаев вместо цилиндрических винтовых передач применяются многозаходные червячные передачи с числом заходов червяка z>4. Передаточное число таких передач, как правило, лежит в диапазоне от 4 до 12,5. При столь малых для червячных передач передаточных числах число заходов червяка z может достигать значения 6-8 при w<8 и 5-6 при 8
Коэффициент диаметра червяка q в проектируемой передаче назначается, в первую очередь, исходя из анализа, имеющегося в наличии зуборезного инструмента и возможностей его применения при изготовлении данной передачи. ГОСТ 19672-74 рекомендует при проектировании червячных передач и червячных фрез следующие значения q = 8; 10; 12,5; 16; 20; 25, реже применяется коэффициенты 9; 11; 12; 14 и 18.
Для малогабаритных передач с межосевым расстоянием aw<80 и числом зубьев z2>40 рекомендуется принимать как можно большие значения коэффициента <7=16-25, поскольку при сочетании этих условий с малыми значениями q слишком малый диаметр впадин червяка может привести к его изгибу или поломке.
После определения межосевого расстояния и выбора числа заходов червяка, числа зубьев колеса и коэффициента диаметра червяка следует выполнить расчет модуля передачи т без учета коэффициента смещения червяка х. В червячных передачах с червяком ZA это осевой модуль, который определяется по формуле: 
Для эвольвентных червячных передач стандартизован и должен быть рассчитан нормальный модуль тп, который определяется по формуле тп=тхcos уь где Yi= atan(zi/<7) - угол подъема витка червяка.
Полученное значение модуля должно быть округлено до ближайшего из стандартных значений. Осевые модули архимедовых червячных передач приводятся в ГОСТ 19672-74.Для эвольвентных червячных передач значения стандартных модулей следует выбирать из перечисленных в ГОСТ 9563-60.
Дальнейший геометрический расчет червячной передачи, выполняется в соответствии с рекомендациями ГОСТ 19650-97. При этом следует учесть, что практически все уравнения в ГОСТе написаны для червячных передач с архимедовыми червяками, в которых основным является осевой модуль тх.
При выполнении геометрического расчета эвольвентной червячной передачи, параметры нормального сечения червяка гпп и ап=20°, необходимо пересчитать в параметры осевого профиля mx=mn/cosyi, ax=atan(tanan/cos yi)
Прежде чем приступить к определению контурных размеров передачи необходимо рассчитать коэффициент смещения червяка х и выполнить проверку на отсутствие подрезания и заострения зубьев колеса. Коэффициент смещения определяется выражением:

Минимально допустимый коэффициент смещения определяется из условия отсутствия подрезания зубьев по формуле:
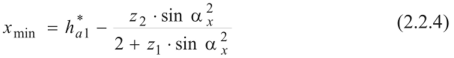
Максимально допустимый коэффициент смещения определяется из условия отсутствия заострения зубьев выражением:
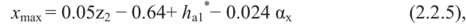
При большом числе зубьев колеса диапазон допустимых значений хт;п<х< хтах, определяемый выражениями (2.2.4) и (2.2.5), получается слишком широким и из конструктивных соображений его следует ограничить значениями -1.5<х<1.
В случае если коэффициент смещения червяка, определяемый выражением (2.2.3), выходит за указанные выше пределы, то необходимо изменить исходные параметры: межосевое расстояние aw, число зубьев колеса z2 или коэффициент диаметра червяка q.
При изменении коэффициента q желательно принимать его не большим, чем коэффициент q0 диаметра производящего червяка из числа имеющихся в производстве червячных фрез. При этом уменьшение коэффициента q по сравнению с q0 позволяет добиться локализации контакта и снизить влияние погрешности межосевого расстояния на качество зацепления в передаче. Однако следует учитывать, что слишком большая разница между q и q0 приводит к необходимости значительного искажения профиля. Подробнее вопросы локализации контакта и методы подбора червячных фрез для червячных колес рассмотрены в 6-й главе.
После внесения необходимых изменений передача должна быть вновь посчитана по выражениям (2.2.3)-(2.2.5).
На рисунке 2.1 показано осевое сечение червячной передачи с архимедовым червяком.
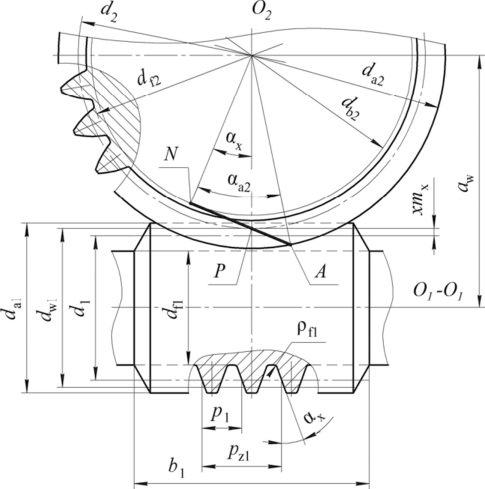
Рис. 2.1. Основные параметры червячной передачи с цилиндрическим червяком типа ZA
Основные параметры и контурные размеры передачи, показанные на рисунке 2.1, рассчитываются по следующим формулам:
Делительный диаметр червяка d= qmx;
Делительный диаметр червячного колеса d2 = z2-mx;
Начальный диаметр червяка dw = (q +2х)-тх;
Угол профиля в нормальном сечении а„= atan(tan ах- cos yi);
Начальный угол подъема yw= atan(z|/(g+2x));
Расчетный шаг червякар=к-тх;
Ход витка червяка рг=р •z.
Диаметр основной окружности колеса в среднем торцовом сечении передачи t/b2=^2'Cos ах;
Выполняя расчет эвольвентной червячной передачи необходимо дополнительно определить:
Основной угол подъема витка yb=acos(cos an cos yi);
Основной диаметр червяка dbi=z-mx/tan уь.
При расчете части контурных размеров червячной передачи с червяком ZA под модулем т подразумевается осевой модуль тх, в то время как для эвольвентных червячных передач в уравнения подставляется нормальный модуль тп. Дальнейший расчет контурных размеров будет выполняться исходя из этого условия.
Высота витка червяка h= h ?т;
Высота головки витка червяка ha= /?а1 -т;
Диаметр вершин витков червяка da=d+2ha*-т
Диаметр вершин зубьев червячного колеса da2=d2+2(ha*+x)m;
Диаметр впадин витков червяка dn=da2h,
Диаметр впадин зубьев колеса d2=d2-2(h - ha —х) ?т;
Угол профиля на вершине зубьев колеса
в среднем сечении aa2=acos (db2/da2);
Радиус выемки /у= 0.5 d—m.
При коэффициенте смещения х>0 наибольший диаметр червячного колеса определяется по формуле: 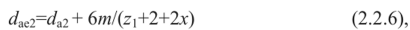
при отрицательном коэффициенте смещения х<0:

Для передач с числом заходов червяка z>4 максимальная ширина колеса b2-0.bl-da, в остальных случаях b2=0.75-da.
Для определения минимальной длины нарезанной части червяка Ь рассчитываются два выражения:
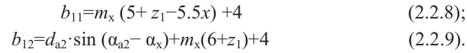
Из полученных значений и Ь2 выбирается большее и округляется до ближайшего целого значения. Из конструктивных соображений допускается увеличение длины нарезаемой части червяка Ь по сравнению с его расчетным значением в 1.2—1.5 раза.
После проверки качества зацепления и определения всех контурных размеров передачи необходимо выполнить расчет контрольных зубоизмерительных параметров червяка и червячного колеса. Полученные зубоизмерительные параметры указываются на рабочих чертежах червяка и колеса. Контрольные зубоизмерительные параметры червяка определяются по выражениям:
Делительная толщина по хорде витка червяка:

Высота до делительной хорды витка:
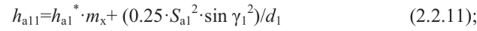
Размер червяка по роликам:
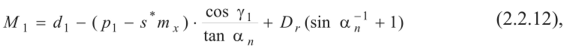
где Д r>1.67mx - диаметр измерительного ролика. Диаметр ролика рекомендуется принимать равный ближайшему большему значению ролика по ГОСТ 2475.
В ГОСТ 19650-97 не предусмотрен расчет зубоизмерительных параметров червячного колеса. Однако указание этих параметров на рабочем чертеже колеса позволяет снизить вероятность возникновения ошибки при нарезке зубьев. Особенно это актуально при изготовлении колеса в качестве запчасти к имеющемуся и частично изношенному червяку.
Зубоизмерительные параметры колеса рекомендуется задавать на диаметре dy2=2-aw-d. При расчете предварительно определяются угол ay2=acos(db2/i/y2) и его инволюта inv ay2=tan ау2-ау2.
Толщина зуба червячного колеса в осевом сечении в средней плоскости передачи определяется выражением:
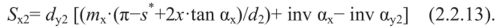
Контролируемая толщина зуба в нормальном сечении:

Высота до измерительной хорды зуба колеса:
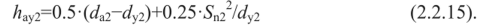
Последняя проверка при выполнении геометрического расчета червячной передачи, которую следует выполнить, это расчет суммарного коэффициента перекрытия е.
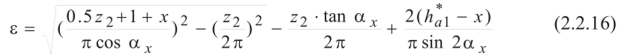
Полученное значение е не должно быть менее единицы.
Венцы червячных колес изготавливаются из материалов с антизадирны- ми и антифрикционными свойствами. Наиболее распространенными являются различные бронзы и латуни, но допускается применение чугуна и даже мягких марок сталей. В малогабаритных передачах с незначительными нагрузками и небольшим числом оборотов червяка могут применяться композиционные металлокерамические материалы, пластмассы, некоторые виды древеснослоистых пластиков (ДСП) и др.
При выборе марки материала венца следует учитывать твердость витков сопряженного червяка, значение и характер изменений нагрузки, скорость скольжения витков, габариты проектируемой передачи и тип применяемой смазки.
Условно материалы, применяемые при изготовлении венцов червячных колес, можно разделить на пять групп:
Группа 1. К этой группе относятся высокооловянные бронзы типа БрОЮФ1, БрОНФ, БрОФЮ-1 и др., которые, кроме олова 6-10%, содержат в качестве основных компонентов фосфор, свинец, цинк, никель, а в некоторых случаях сурьму. Эти бронзы обладают низкой прочностью оь=200-300 МПа, но хорошими антифрикционными свойствами. Особенностью материалов этой группы является мягкое заедание, которое проявляется при работе передачи со значительными перегрузками. Мягкое заедание позволяет избежать задира и намазывания бронзы на червяк, и лишь ускоряет износ зубьев червячного колеса при перегрузках.
Бронзы этой группы в силу их дефицитности рекомендуется применять только в высоконагруженных передачах со скоростью скольжения 12
Группа 2. В группу входят бронзы Бр05Ц5С5, БрОбЦбСЗ, Бр04Ц7С5 и др. По составу они близки к высокооловянным бронзам, входящим в первую группу. Однако содержание олова в них составляет 3-6%, что снижает их ан- тизадирные свойства. Данные бронзы применяются при скорости скольжения vk от 5 до 12 м/с.
Группа 3. В эту группу входят безоловянные бронзы и латуни. Они обладает более высокой прочностью 0Ь=ЗОО-35О МПа, чем оловянные бронзы, но худшими антизадирными свойствами, и широко применяются как более дешевые заменители оловянной бронзы при скоростях скольжения vk<5 м/с.
Алюминиево-железистые бронзы типа БрА10ЖЗМц2 БрА9ЖЗЛ, и т.д. с временным сопротивлением аь>300 МПа допускается использовать только в паре цементированным либо поверхностно упрочненным до твердости HRO45 червяком. При этом, используя такие бронзы, необходимо предусматривать длительную приработку передачи под нагрузкой 25-50% от номинальной. При включении в работу под полной нагрузкой неприработанная передача склонна к возникновению задира.
Более мягкие латуни типа ЛЦ38Мц2С2 с аь<300 МПа допускается применять с улучшенными червяками, твердость которых должна быть не менее 300 НВ.
Группа 4. В нее входят серый чугун СЧ 15-СЧ 20 и высокопрочный чугун АЧС. Применение чугуна в червячных передачах ограничивается скоростью скольжения vk< 1.5-2 м/с. В редких случаях при использовании хромированных червяков скорость скольжения vk может быть увеличена до 2-4 м/с.
Следует помнить, что твердый чугун с аь>300 МПа плохо прирабатывается и склонен к образованию задиров. Оптимальным для изготовления червячных колес является серый чугун с твердостью 140-180 НВ и оь<300 МПа.
Г руина 5. В эту группу входят пластмассы, текстолит и различные пластики типа ДСП. Применение таких материалов допускается только в мало- нагруженных и низкоскоростных передачах при температуре, не превышающей 70-80°С.
Нарезание зубьев червячных колес
Обработка червячных колес до операции зубонарезания не обладает какой-либо принципиальной спецификой по сравнению с обработкой обычных круглых деталей подобного класса.
Используются два способа нарезаний зубьев червячных колес на зубофрезерных станках:
1) червячными фрезами при радиальной или осевой подаче инструмента;
2) резцами-летучками или многозубыми резцами при осевой подаче.
В том и другом способе режущие кромки инструмента должны воспроизводить в пространстве поверхность производящего червяка, находящегося в зацеплении с нарезаемым червячным колесом при том же межосевом расстоянии, что и с рабочим червяком.
Отличие номинального инструментального производящего червяка от рабочего заключается в увеличении (на удвоенную величину радиального зазора) диаметра вершин и гарантированного бокового зазора толщины витков. Кроме того, инструментальный червяк должен иметь закругление витков для образования переходных кривых у основания зубьев нарезаемого червячного колеса.
Шевингование зубьев червячных колес является отделочной операцией и применяется для колес 6-й степени точности и более точных. Шевингование производится после чистового фрезерования.
Червячный шевер представляет собой червяк, геометрия поверхности которого полностью совпадает с геометрией витков рабочего червяка. Режущие свойства шевер приобретает за счет большого числа мелких радиальных канавок, имеющихся на поверхности витков.
Шевингование может выполняться двумя способами: радиальным движением подачи при беззазорном зацеплении (сближением до номинального межосевого расстояния) и окружным движением подачи. В обоих случаях вращение колеса осуществляется вращением фрезы-шевера (механизм привода стола не работает).
При шевинговании способом радиального движения подачи шевер должен иметь толщину витка, равную ширине впадины колеса. При шевинговании колеса способом окружного движения подачи зуб шевера должен входить в зацепление с колесом с зазором в случае установки номинального межосевого расстояния. Шевингование профиля происходит вследствие того, что фреза-шевер ведет (вращает) заготовку колеса, которую в ряде случаев притормаживают. После обработки одной стороны направление вращения шевера изменяется и шевингование производится другой частью шевера, имеющей обратное направление зубьев (насечек).
Иногда в практике нарезания колес для точных передач используют весьма дорогой инструмент, представляющий собой фрезу для осевой подачи, непосредственно переходящую в шевер и даже в притир. Припуск на толщину зубьев червячного колеса под чистовое нарезание червячными фрезами принимают 0,l m и под шевингование 0,03 m.
Использованная литература:
1. Левитан Ю.В., Обморнов В.П., Васильев В.И., Червячные редукторы Справочник. - Ленинград.: Машиностроение, 1985. 168 с.
2. Литвин Ф.Л. Новые виды цилиндрических червячных передач. М.-Л.: Машгиз. 1962. 104 с.
3. Кривенко И.С. Новые типы червячных передач на судах. Л.: Судостроение, 1967. 256 с.
4. Бернацкий И.П. Исследование червячных передач с вогнутым профилем витков червяка, нарезаемых резцом.// Изв. ВУЗов. Машиностроение, 1962, №10, с. 29-37. |
|
|
 Скачать 198.06 Kb.
Скачать 198.06 Kb.