Решение. Контрольная работа по дисциплине "Эконометрика" Номер варианта Студент

• Название: Контрольная работа по дисциплине "Эконометрика" Номер варианта Студент
• Дата: 13.02.2019
• Размер: 48.55 Kb.
• Имя файла: Решение.docx
• Тип: Контрольная работа; #67378

Университет

Факультет заочного обучения
Направление 38.03.01 "Экономика"
Группа ….. Контрольная работа по дисциплине "Эконометрика"

Номер варианта…..

Студент…..
Задание 1. Линейная парная регрессия Построить требуемое уравнение регрессии. Вычислить коэффициент детерминации, коэффициент эластичности, бета коэффициент и дать их смысловую нагрузку в терминах задачи. Проверить адекватность уравнения с помощью F теста. Найти дисперсии оценок и 95% доверительные интервалы для параметров регрессии. Данные взять из таблицы. Найти прогнозируемое значение объясняемой переменной для некоторого значения объясняющей переменной, не заданной в таблице.

Построить уравнение линейной регрессии производительности труда (дет/рабочего) от уровня механизации (в некоторых единицах).

Уровень механизации	20	21	24	33	32	33	36	32	38	43
Производительность труда	32	36	34	43	41	53	56	54	57	61

Решение. По смыслу задачи роль переменной X будет играть уровень механизации, роль переменной Y будет играть производительность труда. Будем строить уравнение регрессии .

Вычислим необходимые средние величины

.

Вычисляя оценки параметров по формулам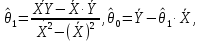


получим, = 1,316, 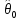= 5,656. В результате искомое уравнение регрессии примет вид .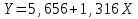

Находя прогнозируемые значения переменной Y и соответствующие остатки регрессии,получим,чтои.

Оценка дисперсии ошибок регрессии равна

.

Найдем




Тогда оценки дисперсии параметров регрессии равны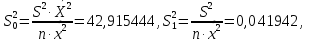



Вычислим коэффициент детерминации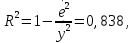



это показывает, что изменение производительности труда на 83,8% объясняется изменением уровня механизации.

Вычислим коэффициент эластичности



это показывает, что при изменении уровня механизации в среднем на 1%, производительность труда изменится в среднем на 0,879% .

Найдем средне квадратические отклонения переменных по формулам 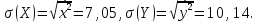Тогда бета коэффициент равен



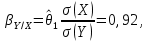это показывает, что при изменении разброса уровня механизации на 7,05 единиц разброс производительности труда изменится на 0,92 от 10,14, то есть на
0,92 *10,14 = 9,28 дет/рабочего.

Проверка адекватности построенного уравнения проведем с помощью F теста проверки гипотезы H₀ : θ₁ = 0 на уровне значимости α = 0,05. Расчетное значение F теста равно



критическое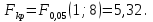

расчетное значение больше критического, следовательно гипотеза H₀ : θ₁ = 0 отвергается и уравнение можно признать адекватным изучаемому процессу.

Найдем 95% доверительные интервалы для параметров регрессии. t_0,05(8) = 2,31, S₀ = 6,551, S₁ = 0,205. Тогда доверительные интервалы примут вид

θ₁ : (0,842; 1,789), θ₀ : (-9,477; 20,789).

Найдем прогнозируемую производительность труда при уровне механизации 44 единицы Y (44) = 5,656+1,316·44 = 63,54 дет/рабочего.
Задание 2. Линейная множественная регрессия. Построить требуемое уравнение регрессии. Вычислить коэффициент детерминации, частные коэффициенты эластичности, частные бета коэффициенты и дать их смысловую нагрузку в терминах задачи. Проверить адекватность уравнения с помощью F теста. Найти оценку матрицы ковариаций оценок параметров регрессии и 95% доверительные интервалы для параметров регрессии. Проверить наличие мультиколлинеарности в модели. Данные взять из таблицы.

Построить уравнение линейной регрессии выручки магазина (в тыс. руб.) от величины торговой площади (кв. м) и количества посетителей в час (чел.).

Торговая площадь	7	9	7,2	7	7,5	8,6	7,2
Количество посетителей	9	8,5	6	9,1	6,6	7,3	8,4
Выручка	14,1	14,9	13	14,9	15	16	14,5

Решение. Искомое уравнение имеет вид Y = θ₀ + θ₁X₁ + θ₂X₂. По смыслу задания имеем, что Y –средний балл, X₁ –количество пропусков, X₂– количество часов в библиотеке.n = 7, k = 2. Введем в рассмотрение матрицы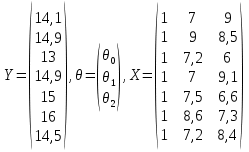



Тогда матрица X^T X примет вид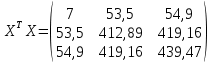



обратная к ней равна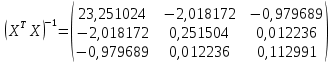



отсюда оценка вектора параметров модели примет вид

В результате искомое уравнение имеет вид

Y=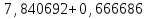X₁+X₂.

Найдем векторы прогноза и остатков регрессии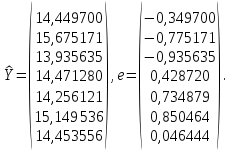



Отсюда находим, что e^T e = 3,047887, и оценка дисперсии ошибок регрессии равна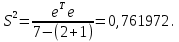

Находя средние величины каждой переменной, получим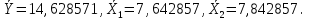

Матрица примет вид, . Тогда

Вычисляя коэффициент детерминации, получим



это показывает, что изменение выручки на 40,4% зависит от изменения торговой площади и количества посетителей, действующих в совокупности.

Находя частные коэффициенты эластичности, получим: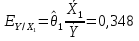



это показывает, что при увеличении торговой площади на 1 % (при неизменном количестве посетителей в торговом центре) выручка вырастет на 0,348%.



это показывает, что при изменении количества посетителей магазина на 1 % (при неизменной торговой площади) выручка изменится на 0,11%.

Находя средне квадратические отклонения переменных получим σ(Y) = 0,854759, σ(X₁) = 0,755659, σ(X₂) = 1,127395.

Частные бета коэффициенты:



это показывает, что при изменении разброса торговых площадей на 0,756 кв.м. (при неизменном количестве посетителей) разброс выручки изменится на 0,589 тыс. руб. от 0,855, то есть на 0,589 · 0,855 = 0,504 тыс. руб.



это показывает, что при изменении разброса количества посетителей на 1,127 чел (при неизменной торговой площади) разброс выручки изменится на 0,285 от 0,855, то есть на 0,285 · 0,855 = 0,243 тыс. руб.

Проверка адекватности построенного уравнения проведем с помощью F теста проверки гипотезы H₀ : θ₁ = θ₂ = 0. Расчетное значение F теста найдем по формуле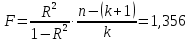



Критическое



Поскольку расчетное значение меньше критического, то гипотеза H₀ : θ₁ = θ₂ = 0 принимается и уравнение Y = θ₀ + θ₁X₁ + θ₂X₂ нельзя считать адекватным изучаемому процессу.

Задание 3. Введение в анализ временных рядов. Проверить ряд на наличие тренда. Сгладить ряд методом простой скользящей средней (m = 3), экспоненциальным сглаживанием (α = 0,3, α = 0,8). Построить исходный и сглаженные ряды. На основании построенных рядов определить вид трендовой модели. Построить трендовую модель. Сделать прогноз изучаемого признака на два шага вперед.

Ряд данных

152;141;130;127;119;110;103;95;91;79;72;65;57;48;43;35;28;20;13;6

Решение. Проверим ряд на наличие тренда с помощью метода Фостера-Стъюарта.

1) Построим две последовательности {k_t},{l_t}. Результаты оформим в виде таблицы

yt	152	141	130	127	119	110	103	95	91	79	72	65	57	48	43	35	28	20	13	6
kt	-	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
lt	-	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1

Вычислим сумму



2) Проверим выполнение гипотезы H₀ : g = μ,спомощью статистики Стьюдента. По таблице определяем, что μ = 5,195, σ = 1,677. Вычислим расчетное значение статистики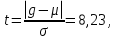



которое сравнивается с критическим t_kp= t_0,05(18) = 2,10. Расчетное значение больше критического, то гипотеза H₀ отвергается и в рассматриваемом ряду тренд есть.

Сгладим ряд методом простой скользящей средней, так как m = 3, то формула для получения сглаженных уровней примет вид: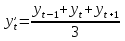



при этом теряем первый и последний уровни.

В результате получим ряд: 141; 132,7; 125,3; 118,7; 110,7; 102,7; 96,3; 88,3; 80,7; 72; 64,7; 56,7; 49,3; 42; 35,3; 27,7; 20,3; 13.

Проведем экспоненциальное сглаживание при α = 0,3. В этом случае формула для сглаживания ряда примет вид: y_t^′ = 0, 3y_t +0, 7y_t^′₋₁ в качестве нулевого сглаженного уровня возьмем среднее первых двух уровней исходного ряда, то есть y₀^′ = 146,5.

В результате получим ряд: 148,2; 146; 141,2; 136,9; 131,6; 125,1; 118,5; 111,4; 105,3; 97,4; 89,8; 82,4; 74,7; 66,7; 59,6; 52,2; 45; 37,5; 30,1; 22,9.

Проведем экспоненциальное сглаживание при α = 0,8. В этом случае формула для сглаживания ряда примет вид: y_t^′ = 0, 8y_t +0, 2y_t^′₋₁ в качестве нулевого сглаженного уровня возьмем среднее первых двух уровней исходного ряда, то есть y₀^′ = 146,5.

В результате получим ряд: 150,9; 143; 132,6; 128,1; 120,8; 112,2; 104,8; 97; 92,2; 81,6; 73,9; 66,8; 59,0; 50,2; 44,4; 36,9; 29,8; 22; 14,8; 7,8.

Построим исходный и сглаженные ряды. Смотрим рис 1.
Рис. 1: ряд 1 - исходный ряд, ряд 2 - сглаженный методом простой скользящей средней, ряд 3 - сглаженный экспоненциально при α = 0,3, ряд 4 - сглаженный экспоненциально при α = 0,8
На основе построенных: исходного, сглаженных рядов можно сделать предварительный вывод о линейном виде трендовой модели.

Определим коэффициенты модели y_t = a₀+a₁t с помощью МНК. Вычислим необходимые суммы, тогда система нормальных уравнений примет вид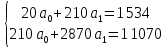



Решая эту систему, получим оценки неизвестных параметров

Искомая трендовая модель имеет вид y_t=156,23-7,57t. Найдем прогнозируемые значения на два шага вперед