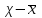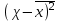Решение Группы магазинов по торговой площади, кв м
 Скачать 192.36 Kb. Скачать 192.36 Kb.
|
Задача 23С целью изучения вариации размеров торговой площади магазинов произведено 5%-ное выборочное обследование по методу случайного бесповторного отбора. Результаты обследования представлены следующими данными:
Определите: 1) средний размер торговой площади одного магазина; 2) дисперсию и среднее квадратическое отклонение; 3) коэффициент вариации; 4) с вероятностью 0,997 предельную ошибку выборки, а также интервал, в котором находится средний размер торговой площади всех магазинов. Сделайте выводы. Решение:
1. Рассчитаем средний размер торговой площади одного магазина, применив формулу средней арифметической взвешенной: 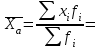 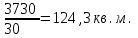 2. Расчет дисперсии и среднего квадратического отклонения проведем на основе данных следующей таблицы:
Для определения среднего квадратического отклонения используем формулу 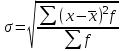 = =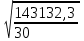 =69,07% =69,07%Так как среднее квадратическое отклонение есть корень квадратный из дисперсии, то дисперсия равна 4771,1. Коэффициент вариации: 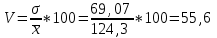 Колеблемость торговой площади в каждом магазине от среднего процента торговой площади довольно значительна, то есть средняя величина не совсем типична для данной совокупности. Определим с вероятностью 0,997 предельную ошибку выборки, а также интервал, в котором находится средний размер торговой площади всех магазинов. 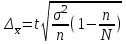 Коэффициент доверия при вероятности 0,997 равен 3. Генеральная совокупность N=600, совокупность единиц, отобранных для выборочного наблюдения, n=30. 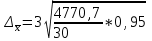 =36,9 =36,9Вычислим пределы стоимости для всех заводов:  - -  + +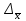 124,3-36,9 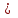 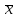 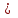 124,3+36,9 124,3+36,987,4% 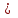 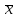 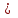 161,2% 161,2%С вероятностью 0,997 можно утверждать, что средняя торговая площадь колеблется в пределах от 87,4% до 161,2%. Задача 2 Имеются следующие данные по предприятиям отрасли:
Для изучения зависимости между стоимостью основных производственных фондов и объемом продукции произведите группировку предприятий по стоимости основных производственных фондов, образовав четыре группы с равными интервалами. По каждой группе и в целом по совокупности подсчитайте: 1) число предприятий; 2) стоимость основных производственных фондов – всего и в среднем на одно предприятие; 3) стоимость продукции – всего и в среднем на одно предприятие; 4) фондоотдачу 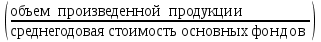 . .Результаты представьте в разработочной и групповой таблицах. Дайте анализ показателей таблицы и сделайте краткие выводы. Решение: Сделаем группировку по стоимости ОПФ. По условию образуем 4 группы с равными интервалами. Находим размер интервала: 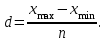 Где d – размер интервала; 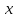 mах, ( mах, (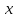 min) - максимальное (минимальное) значение группировочного признака в совокупности; min) - максимальное (минимальное) значение группировочного признака в совокупности;n - число единиц в совокупности. Тогда, 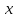 mах = 7 (млн. руб.); mах = 7 (млн. руб.);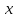 min = 1 (млн. руб.); min = 1 (млн. руб.);n = 4; d = (7-1)/4 = 1.5 (млн. руб.). Отграничим каждую группу предприятий, обозначив нижнюю границу каждого следующего интервала числом на 0,1 большим верхней границы предшествующего интервала. Получим следующие 4 группы: – [1,0-2,5] – [2,6-4,0] – [4,1-5,5] – [5,6-7,0] Занесем полученные данные в разработочную таблицу. Таблица 2
По данным таблицы 2 получим: Число предприятий в группах: I – 4 предприятия; II – 8 предприятий; III – 4 предприятия; IV – 4 предприятия; Всего 20 предприятий. Стоимость всех основных производственных фондов составляет 78,5 млн. руб., а в среднем на одно предприятие 78,5/20 = 3,925 млн. руб. Стоимость продукции – всего 96 млн. руб. и в среднем на одно предприятие 96/20 = 4,8 млн. руб. Рассчитаем средние показатели по каждой группе, данные занесем в аналитическую таблицу: Таблица 3
Фондоотдача в среднем на одно предприятие в группе составляет: 2,6/1,8 = 1,44 3,4/3,5 = 0,97 4,8/4,6 = 1,04 9,9/6,3 = 1,57 Результаты расчетов показывают, что с увеличением среднегодовой стоимости основных производственных фондов увеличиваются объемы произведенной продукции, т.е. чем выше стоимость ОПФ предприятия, тем больший объем продукции может быть произведен, а соответственно увеличится и фондоотдача. Задача 12 Данные о численности населения области на начало года (тыс. чел.):
Определите: 1) относительные величины структуры (долю городского и сельского населения в общей численности по годам); 2) относительные величины координации (число городского населения на 100 человек сельского); 3) относительные величины динамики численности всего населения в процентах к его численности по первому году. Решение: 1) Относительная величина структуры (ОВС) характеризует структуру совокупности, определяет долю (удельный вес) части в общем объеме совокупности. ОВС рассчитывают как отношение объема части совокупности к абсолютной величине всей совокупности, определяя тем самым удельный вес части в общем объеме совокупности (%): 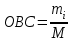 , где mi- объем исследуемой части совокупности, M – общий объем исследуемой совокупности. , где mi- объем исследуемой части совокупности, M – общий объем исследуемой совокупности.Для 1 года: ОВС = 1810/2890*100% = 62,63% ОВС = 1080/2890*100% = 37,37% Для 2 года: ОВС = 1890/2960*100% = 63,85% ОВС = 1070/2960*100% = 36,15% Для 3 года: ОВС = 2065/3130*100% = 65,97% ОВС = 1065/3130*100% = 34,03% Для 4 года: ОВС = 2033/3100*100% = 65,58% ОВС = 1067/3100*100% = 34,42% 2) Относительная величина координации (ОВК) характеризует соотношение между двумя частями исследуемой совокупности, одна из которых выступает как база сравнения (%): 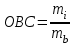 , где mi- одна из частей исследуемой совокупности, mb- часть совокупности, которая является базой сравнения. , где mi- одна из частей исследуемой совокупности, mb- часть совокупности, которая является базой сравнения.В нашем случае, базой сравнения является численность сельского населения, значит: Для 1 года ОВК = 1810/1180*100% 168 человек (На 100 жителей сельского населения приходится 168 городского); Для 2 года ОВК = 1890/1070*100% 177 человек; Для 3 года ОВК = 2065/1065*100% 194 человек; Для 4 года ОВК = 2033/1067*100% 191 человек; 3) Относительная величина динамики (ОВД) характеризует изменение объема одного и того же явления во времени в зависимости от принятого базового уровня. ОВД рассчитывают как отношение уровня анализируемого явления или процесса в текущий момент времени к уровню этого явления или процесса за прошедший период времени. В результате получаем коэффициент роста, который выражается кратным отношением. При исчислении этой величины в процентах, (результат умножается на 100) получаем темп роста. Темпы роста можно просчитывать как с постоянным базовым уровнем (базисные темпы роста-ОВДб ), так и с переменным базовым уровнем (цепные темпы роста - ОВДц) 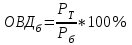 где РТ - уровень текущий; Рб - уровень базисный; 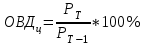 где РТ - уровень текущий; РТ-1 - уровень, предшествующий текущему; По условию задачи, рассчитываем ОВД, исходя из численности 1 года, следовательно считаем, тогда: Для 2 года = 2960/2890*100% = 102,4 % (темп роста населения за второй год увеличился на 2,4 %); Для 3 года = 3130/2890 = 108,3% (темп роста населения за второй год увеличился на 8,3 %); Для 4 года = 3100/2890 = 107,3% (темп роста населения за второй год увеличился на 7,3 %). Задача 17 По приведенным данным рассчитайте среднюю урожайность зерновых с одного гектара в хозяйстве за каждый год:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||