Решение Группы магазинов по торговой площади, кв м
 Скачать 192.36 Kb. Скачать 192.36 Kb.
|
|
Исчислите динамические коэффициенты эластичности по продовольственным и непродовольственным товарам. Сделайте выводы. Решение: Коэффициент эластичности - это отношение темпа прироста спроса к темпу прироста какого - либо факторного признака (цен, доходов населения и пр.) Показатели коэффициента эластичности предварительно рассчитываются на душу населения. Таким образом, коэффициент эластичности можно записать: 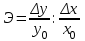 (1) (1)или 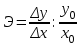 (2) (2)Так как 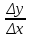 есть производная функции у(х), то коэффициент эластичности может быть записан так: есть производная функции у(х), то коэффициент эластичности может быть записан так: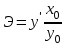 (3) (3)Введенные обозначения: 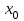 - факторный признак (уровень цен, среднедушевой доход) в прошедшем периоде; - факторный признак (уровень цен, среднедушевой доход) в прошедшем периоде;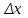 - его прирост; - его прирост;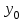 - результативный показатель (продажа или потребление) в прошедшем периоде; - результативный показатель (продажа или потребление) в прошедшем периоде;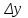 - его прирост. - его прирост.В зависимости от исходной информации коэффициенты эластичности делятся на динамические и статические. Динамические коэффициенты эластичности вычисляются на основе данных об изменении спроса во времени. Исчислим динамические коэффициенты эластичности: а) по продовольственным товарам Э = 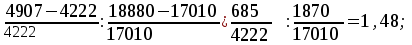 б) по непродовольственным товарам Э = 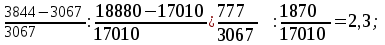 То есть рост душевого дохода на 1% вызывает рост спроса на продовольственные товары на 1,48%, а на непродовольственные товары на 2,3%. Задача 122Данные о доходах бюджета области за три года, млн.р.: Таблица 1.
Измерьте сезонные колебания доходов бюджета по кварталам, рассчитав индексы сезонности методом простой средней. Изобразите сезонную волну графически. Сделайте выводы. Решение: Для расчета индекса сезонности методом простой средней используем формулу (1):  (1) (1)где  - средний доход бюджета области для каждого квартала за три года; - средний доход бюджета области для каждого квартала за три года;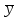 - общий средний квартальный доход за три года. - общий средний квартальный доход за три года.Совокупность индексов сезонности образует сезонную волну, характеризующую внутригодовые повторяющиеся колебания доходов бюджета, т.е. внутригодовую цикличность. Индексы сезонности могут быть использованы в прогнозировании доходности бюджета на следующие годы по кварталам. Для этого вначале определяют прогнозируемый средний квартальный уровень ( 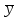 прог), исходя из ожидаемого дохода за год (Рпрог): прог), исходя из ожидаемого дохода за год (Рпрог): 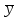 прог=Рпрог: 12, прог=Рпрог: 12,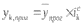 , а затем умножают его на соответствующие индексы сезонности по кварталам. , а затем умножают его на соответствующие индексы сезонности по кварталам.Таблица 2.
На рис.1 представлено графическое изображение сезонной волны по п. 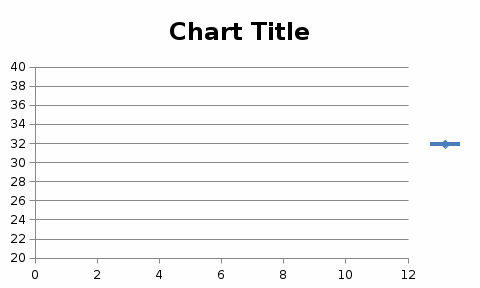 Рис.1. Сезонная волна по доходам бюджета Результаты проведенных расчетов позволяют сделать следующие выводы. Данные таблицы 2 и рис.1 показывают, что минимальный доход бюджета приходится на 1 квартал, а максимальный – за 4. Прогнозирование уровней ряда в данном случае проводят путем умножения выровненных месячных уровней на индексы сезонности. Список литературы 1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1995. 2. Ефимова М.Р. Практикум по общей теории статистики: учебное пособие. – М.: Финансы и статистика, 2003. 3. Практикум по теории статистики: Учебное пособие / Под ред. Р.А. Шмойловой. – М: Финансы и статистика, 1999. 4. Курс социально-экономической статистики: Учебник / Под ред. проф. М.Г. Назарова. – М.: Финстатинформ, ЮНИТИ-ДАНА, 2000. Задача 135 Средняя месячная заработная плата работников в отчетном периоде выросла по сравнению с базисным на 15 %. Покупательная способность рубля снизилась на 8 %. Определите, как изменилась реальная заработная плата. Приведите формулы используемых индексов и укажите их взаимосвязь. Решение: Средняя заработная плата связана с фондом оплаты труда и среднесписочной численностью формулой 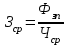 поэтому так же связаны индексы этих показателей, т.е. 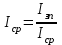 По условию задачи фонд заработной платы увеличился на 15%, т.е. Фзп.от=1,15Фзп.б., а численность работников сократилась на 8%, т.е. Чср.от=0,92Чср.б., поэтому  или 125%, т.е. средняя заработная плата возросла на 25%. или 125%, т.е. средняя заработная плата возросла на 25%.Список литературы Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1995. Ефимова М.Р. Практикум по общей теории статистики: учебное пособие. – М.: Финансы и статистика, 2003. Практикум по теории статистики: Учебное пособие / Под ред. Р.А. Шмойловой. – М: Финансы и статистика, 1999. Курс социально-экономической статистики: Учебник / Под ред. проф. М.Г. Назарова. – М.: Финстатинформ, ЮНИТИ-ДАНА, 2000. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
