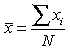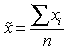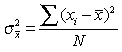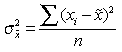Выборочное наблюдение. Методы сплошного и выборочного наблюдения социальноэкономических явлений и процессов
 Скачать 53 Kb. Скачать 53 Kb.
|
|
Методы сплошного и выборочного наблюдения социально-экономических явлений и процессов Общие понятия о сплошном и выборочном наблюдении Выборочное наблюдение является одним из наиболее широко применяемых видов несплошного наблюдения. В основе выборочного наблюдения лежит идея о том, что отобранная в случайном порядке некоторая часть единиц может представлять всю изучаемую совокупность явления по интересующим исследователя признакам. Целью выборочного наблюдения является получение информации для определения сводных обобщающих характеристик всей изучаемой генеральной совокупности. При проведении выборочного наблюдения должны соблюдаться следующие принципы отбора единиц совокупности: 1) обеспечение случайности — при отборе каждой из единиц изучаемой совокупности обеспечивается равная возможность попасть в выборку; при этом случайный отбор — это не беспорядочный отбор, а отбор при соблюдении определенной методики, например, осуществление отбора по жребию; 2) обеспечение достаточного числа отобранных единиц - отобранная из всей изучаемой совокупности часть должна быть репрезентативной (представительной) в отношении тех признаков, которые изучаются или оказывают существенное влияние на формирование сводных обобщающих характеристик. В выборочном наблюдении также используются следующие понятия: 1) генеральная совокупность — совокупность единиц, подлежащая изучению по интересующим исследователя признакам; 2) выборочная совокупность — случайно выбранная из генеральной совокупности некоторая ее часть. Основные характеристики генеральной и выборочной совокупностей представлены в таблице 5.1. Таблица 5.1 - Основные характеристики генеральной и выборочной совокупностей
Система правил отбора и способов характеристики единиц изучаемой совокупности составляет содержание выборочного метода, суть которого состоит в получении первичных данных при наблюдении выборки с последующим обобщением, анализом и их распространением на всю генеральную совокупность с целью получения достоверной информации об исследуемом явлении. Репрезентативность выборки при этом обеспечивается соблюдением принципа случайности отбора объектов совокупности в выборку. Идеальным вариантом систематического наблюдения за объектом является сочетание относительно редких сплошных обследований типа переписей с систематическим несплошным наблюдением. Кроме того, очень эффективно и широко распространено на практике параллельное использование сплошного и несплошного наблюдения, когда одновременно со сплошным наблюдением по узкой программе часть единиц наблюдения обследуется по более широкой программе. Ошибки выборочного наблюдения. Предельная теорема, предельная ошибка Между признаками выборочной совокупности и генеральной совокупности, как правило, существует некоторое расхождение, которое называется ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин: 1) ошибки регистрации или технические ошибки связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т.п; 2) под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и разыскиваемой истинной характеристикой генеральной совокупности: а) систематические ошибки связаны с нарушением установленных правил отбора; б) случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. В результате систематической ошибки выборка легко может оказаться смещенной, т.к. при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, являясь постоянной частью ошибки репрезентативности, она увеличивается с увеличением объема выборки. Размер ошибки смещения определить очень сложно, иногда невозможно. Ошибки смещения бывают преднамеренные и непреднамеренные. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появления такой ошибки, необходимо соблюдать принцип случайности отбора единиц. Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появления таких ошибок, необходима хорошая основа выборки. Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности; с увеличением объёма выборки случайная ошибка уменьшается. Теоретическим обоснованием работы со случайными ошибками выборки является теория вероятностей и ее предельные теоремы. Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Поскольку случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала. Случайный отбор может быть бесповторным и повторным. При бесповторном отборе единица, попавшая в выборочную совокупность, обратно в генеральную не возвращается. Следовательно, численность генеральной совокупности всё время уменьшается (по такой схеме проходят, например, тиражи различных лотерей). При повторном отборе отобранная единица наблюдения возвращается в генеральную совокупность обратно. Таким образом, численность генеральной совокупности в процессе Формирование выборочной совокупности. Определение необходимого объёма выборки Как уже было отмечено, для репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц. Если совокупность является качественно однородной, то принцип случайности реализуется простым случайным отбором объектов выборки. Простым случайным отбором называют такую процедуру образования выборки, которая обеспечивает для каждой единицы совокупности одинаковую вероятность быть выбранной для наблюдения для любой выборки заданного объема. Простой случайный отбор может осуществляться или с помощью жеребьёвки, или при помощи выбора случайных чисел из специальных таблиц. Механический отбор применяется в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.). При этом выбирается каждый N-ый элемент генеральной совокупности. Если единицы не ранжированы относительно изучаемого признака, то первый элемент выбирается наугад, а если ранжированы – то из середины первой сотни. При большой совокупности данных этот способ отбора близок к собственно случайному. Для определения средней ошибки механической выборки используется формула средней ошибки при собственно случайном бесповторном отборе. Типический (стратифицированный, расслоенный) отбор используется, когда все единицы неоднородной генеральной совокупности можно разбить на несколько типических групп. При исследовании населения такими группами могут быть районы, социальные, возрастные или образовательные группы и т.д. Типический отбор предполагает выборку единиц из каждой группы собственно случайным или механическим способом. Собственно случайный, механический и типический (стратифицированный, расслоенный) отборы относятся к разновидности индивидуальных отборов. Серийный (гнездовой) отбор применяется в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. Например: упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и.т.п. Сущность серийной выборки заключается в собственно случайном либо механическом отборе серий, внутри которых производится сплошное исследование единиц. Серийный (гнездовой) отбор относится к разновидности групповых отборов. Комбинированный отбор — это комбинация рассмотренных выше способов отбора. Отдельно выделяют многоступенчатый отбор - это образование внутри генеральной совокупности вначале крупных групп единиц, из которых образуются группы, меньшие по объему, и так до тех пор, пока не будут отобраны те группы или отдельные единицы, которые необходимо исследовать. Понятие малой выборки При большом числе единиц выборочной совокупности (n >100) распределение случайных ошибок выборочной средней в соответствии с теоремой А.М. Ляпунова нормально или приближается к нормальному по мере увеличения числа наблюдений. Однако в практике статистического исследования в условиях рыночной экономики все чаще приходится сталкиваться с малыми выборками. Малой выборкой называется такое выборочное наблюдение, численность единиц которого не превышает 30. Разработка теории малой выборки была начата английским статистиком В.С. Госсетом (печатавшимся под псевдонимом Стьюдент). Он доказал, что оценка расхождения между средней малой выборки и генеральной средней имеет особый закон распределения. |