Практическое занятие 3. Ошибки выборки 1 Ошибки регистрации и ошибки репрезентативности
 Скачать 81.05 Kb. Скачать 81.05 Kb.
|
Практическое занятие №3. Ошибки выборки3.1 Ошибки регистрации и ошибки репрезентативностиВ результате статистической обработки данных могут возникнуть ошибки наблюдения, получаемые вследствие расхождения между величиной какого-либо показателя, найденного при статистическом наблюдении данных и действительными его размерами. Их еще называют выбросами. Это данные среди исходных результатов измерений (или данные, занесенные в таблицу и полученные из результатов измерений), которые настолько отклоняются от сопоставимых данных, внесенных в ту же самую таблицу, что признаются несовместимыми. В зависимости от причин возникновения различаю ошибки регистрации и ошибки репрезентативности. Ошибки регистрации возникают в результате неправильного установления фактов или ошибочной записи в процессе наблюдения. Они бывают случайными и систематическими. Случайные ошибки регистрации могут быть допущены как в опрашиваемыми в их ответах, так и регистраторами. Систематические ошибки могут быть и преднамеренными, и непреднамеренными. Преднамеренные ошибки – сознательные, тенденциозные искажения действительного положения дел. Непреднамеренные ошибки могут быть вызваны различными случайными причинами (небрежность, невнимательность). Ошибки репрезентативности (представительности) возникают в результате неполного обследования и в случае, если обследуемая совокупность недостаточно полно воспроизводит генеральную совокупность. Они могут быть случайными и систематическими. Ошибки репрезентативности присущи выборочному наблюдению и возникают в связи с тем, что выборочная совокупность не полностью воспроизводит генеральную. Выборка является репрезентативной (или представительной), если она достаточно полно представлять изучаемые признаки генеральной совокупности. Условием обеспечения репрезентативности выборки является, согласно закону больших чисел, соблюдение случайности отбора, т.е. все объекты генеральной совокупности должны иметь равные вероятности попасть в выборку. Анализ репрезентативности выборки особенно важен на начальном этапе исследований, когда численность генеральной совокупности неизвестна, но известны некоторые параметры опыта, позволяющие оценить репрезентативность. Ошибки выборки – разность между характеристиками выборочной и генеральной совокупностей. Для среднего значения определяют предельную ошибку выборки по формуле 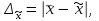 (3.1) (3.1)где 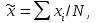 (3.2) (3.2)N– объем выборки. Грубые ошибки и промахи обнаруживают и исключают из расчетов следующим образом: находят среднее арифметическое 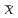 результата n-кратного измерения величины хi; результата n-кратного измерения величины хi;определяют среднее квадратическое отклонение S; Если базовый элемент ijсодержит лишь два результата измерений, то внутриэлементное расхождение (аналог стандартного отклонения) равно 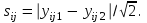 (3.3) (3.3)Таким образом, если во всех базовых элементах содержится по два результата измерений, для простоты вместо стандартных отклонений могут быть использованы абсолютные расхождения; вычисляют вспомогательную величину t(S) (табл. 3.1). Таблица 3.1 – Значения вспомогательной величины t(S) в зависимости от числа nповторных измерений (степень достоверности 0,95)
При |хi - 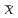 |>t(S) результат измерения хiявляется грубой ошибкой, поэтому его исключают из расчетов и среднее значение |>t(S) результат измерения хiявляется грубой ошибкой, поэтому его исключают из расчетов и среднее значение 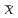 вычисляют заново для оставшихся достоверных результатов измерения. вычисляют заново для оставшихся достоверных результатов измерения. Ошибки (промахи) могут быть исключены из генеральной совокупности с помощью следующего правила: если некоторое измерение xi внушает сомнение в его принадлежности к генеральной совокупности, в этом случае определяется значение  и S генеральной совокупности без сомнительных измерений; и S генеральной совокупности без сомнительных измерений;используя правило Томпсона (критерий Рошера) вычисляется коэффициент k = (xi –  )/S. )/S.Если k больше допустимого значения, то делается вывод о том, что xi не принадлежит к генеральной совокупности. Значения допустимых k дано в таблице 3.2. Таблица 3.2 – Значения допустимых kв зависимости от числа измерений
В литературе известны также критерии 3s, Граббса (Смирнова) [ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений], Шарлье, Шовенэ, Диксона и др., которые позволяют исключить грубые промахи. 3.2 Критерий РомановскогоИспользуя критерий Романовского можно определить грубую погрешность в зависимости от числа измерений и уровня значимости α. Для этого необходимо вычислить расчетное значение Vрасч сомнительного результата по формулам: 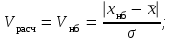 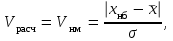 (3.4) (3.4)где Vнб, Vнм – соответственно расчетные значения соответствующие наибольшему (хнб) и наименьшему (хнм) значениям сомнительного результата. Для принятых значений числа измерений n и уровня значимости α определяется максимально допустимое значение Vдоп по таблице 3.3, которое сравнивается с расчетным. Если Vдоп<Vрасч, то сомнительные значения (хнб, хнм) являются грубыми погрешностями и должны быть исключены из дальнейших рассмотрений. Если Vдоп>Vрасч, то хнб и хнм необходимо оставить в данном ряду измерений и учитывать при обработке результатов измерений. Таблица 3.3 – Значение критерия Романовского Vдоп в зависимости от числа измерений и уровня значимости
Пример 3.1. Проверить результат хнб = 17,15 на соответствие грубой погрешности при =0,05. Выполнено измерений п = 12; разброс значений составил = 0,03, 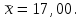 Решение. Рассчитаем критерий Романовского по формуле (3.4): Vрасч = (17,15 – 17,00)/0,03 = 5. Для заданных = 0,05 и п = 12 найти по таблице 3 допустимое значение критерия Романовского Vдоп = 2,39. Сравнивая табличное значение с расчетным, получаем 2,39<5, т.е. Vдоп<Vрасч, следовательно, хнб является грубой погрешностью и должно быть исключено из дальнейших рассмотрений. 3.3 Статистическая обработка экспериментальных данных. Собственно-случайная выборка (простая случайная)Выборочное наблюдение относится к разновидности несплошного наблюдения, цель которого – по отобранной части единиц дать характеристику всей совокупности единиц. Необходимо, чтобы отобранная часть была репрезентативна (т.е. представляла всю совокупность единиц). Используя теорему Чебышева П.Л. можно вычислить величину 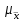 , выражающую среднее квадратическое отклонение выборочной средней от математического ожидания: , выражающую среднее квадратическое отклонение выборочной средней от математического ожидания: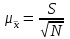 , (3.5) , (3.5)которую называют средней ошибкой выборки. С учетом выбранного уровня вероятности и соответствующего ему значения t (выбирается по табл. 2.5) предельная ошибка выборки составит: 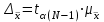 , (3.6) , (3.6)где tα(N-1) – квантиль распределения Стьюдента для вероятности α и числа степеней свободы f = (N-1). С учётом (3.5) и (3.6) можно утверждать, что при заданной вероятности генеральная средняя 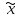 будет находиться в следующих границах: будет находиться в следующих границах: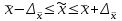 (3.7) (3.7)Пример 3.2. Предположим, в результате выборочного обследования жилищных условий жителей города, осуществленного на основе собственно-случайной повторной выборки, получен следующий ряд распределения (табл. 3.4). Таблица 3.4 – Результаты выборочного обследования жилищных условий жителей города
Рассмотрим определение границ генеральной средней, в данном случае – средней площади жилищ в расчёте на 1 чел. в целом по городу, опираясь только на результаты выборочного обследования. Для определения средней ошибки выборки нам необходимо, прежде всего, рассчитать выборочную среднюю величину и дисперсию изучаемого признака (табл. 3.5). В случае, когда данные сгруппированы по интервалам, т. е. представлены в виде интервальных рядов распределения, при расчёте средней арифметической в качестве значения признака принимают середину интервала, исходя из предположения о равномерном распределении единиц совокупности на данном интервале. Таблица 3.5 – Расчёт средней (полезной) площади жилищ, приходящейся на 1 чел., и дисперсии
Расчёт ведется по формулам: 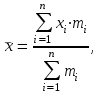 (3.8) (3.8)где xi – середина интервала. В нашем примере: 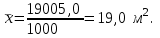 Дисперсию определим по формуле: 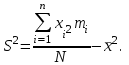 (3.9) (3.9)Тогда получаем: 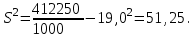 Откуда получаем значение выборочного среднего квадратичного отклонения: S = 7,16м2. Средняя ошибка выборки составит: 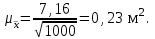 Определим предельную ошибку выборки с вероятностью 0,954 (t=2): 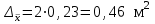 . .Установим границы генеральной средней: 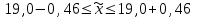 или или 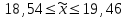 . .Таким образом, на основании проведенного выборочного обследования с вероятностью 0,954 можно заключить, что средний размер общей площади, приходящейся на 1 чел., в целом по городу лежит в пределах от 18,5 до 19,5 м2. При расчёте средней ошибки собственно-случайной бесповторной выборки необходимо учитывать поправку на бесповторность отбора: 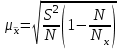 , (3.10) , (3.10)где Nx – генеральная совокупность. Если предположить, что представленные в таблице 6 данные являются результатом 5%-го бесповторного отбора (следовательно, генеральная совокупность включает 20 000 ед.), т.е. средняя ошибка выборки согласно (3.10) будет несколько меньше: 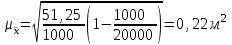 . .Соответственно уменьшится и предельная ошибка выборки, что вызовет сужение границ генеральной средней. Особенно ощутимо влияние поправки на бесповторность отбора при относительно большом проценте выборки. Варианты заданий к практическому занятию №3
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||