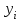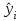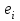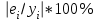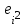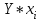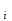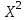Эконометрика. Контрольная работа по дисциплине Эконометрика
 Скачать 331.35 Kb. Скачать 331.35 Kb.
|
1 2 7. Представить графически фактические и модельные значения Y точки прогноза. Воспользуемся данными из таблицы 2 для построения графиков с помощью MS Excel. 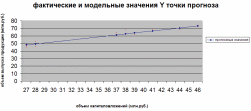 Рис. 2. Фактические и модельные значения Y точки прогноза. 8. Составить уравнения нелинейной регрессии: гиперболической, степенной, показательной. Привести графики построенных уравнений регрессии. Построение степенной модели. Уравнение степенной модели имеет вид: 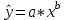 Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения: 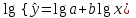 Обозначим 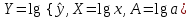 . .Тогда уравнение примет вид 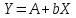 – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 1: – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 1:Таблица 8. Расчет параметров уравнения степенной модели регрессии.
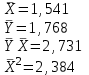 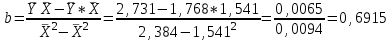 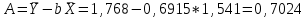 Уравнение регрессии будет иметь вид: 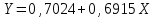 Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения: 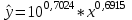 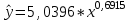 Вычислим коэффициент детерминации 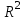 : :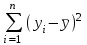 =930,4; =930,4; 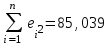 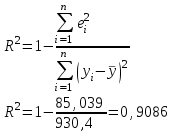 (1) (1)Вычислим среднюю ошибку аппроксимации А: 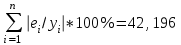 % %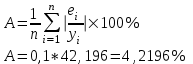 (2) (2)Коэффициент эластичности рассчитывается по формуле: 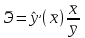 (3) (3)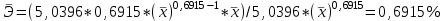 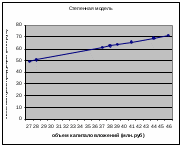 Рис. 3. График степенного уравнения регрессии. Построение показательной функции. Уравнение показательной кривой: 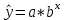 Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения: 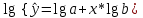 Обозначим 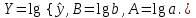 Получим линейное уравнение регрессии: 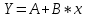 Рассчитаем его параметры, используя данные таблиц 1 и 8. 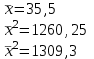 Промежуточные расчеты представим в таблице 9. Таблица 9. Промежуточные расчеты для показательной функции.
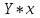 =63,2432 =63,2432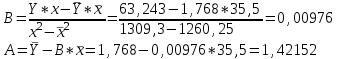 Уравнение будет иметь вид: 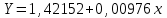 Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения: 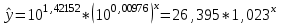 Рассчитаем коэффициент детерминации по формуле (1). 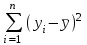 =930,4; =930,4; 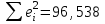 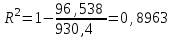 Вычислим среднюю ошибку аппроксимации А по формуле (2): 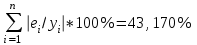 А=0,1*43,170=4,317% Коэффициент эластичности рассчитаем по формуле (3): 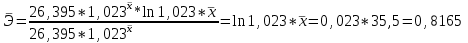 % %Построим график функции с помощью MS Excel. 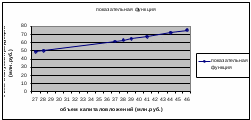 Рис. 4. График показательного уравнения регрессии. Построение гиперболической функции. Уравнение гиперболической функции 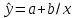 Произведем линеаризацию модели путем замены Х=1/х. В результате получим линейное уравнение: 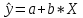 Рассчитаем параметры уравнения, промежуточные вычисления представим в таблице 10. Таблица 10. Расчет параметров для гиперболической модели.
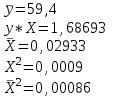 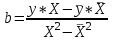 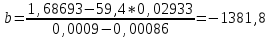 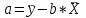 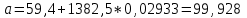 Уравнение гиперболической модели: 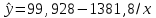 Рассчитаем коэффициент детерминации по формуле (1). 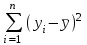 =930,4; =930,4; 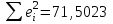 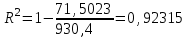 Вычислим среднюю ошибку аппроксимации А по формуле (2): 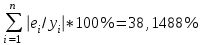 А=0,1*38,1488=3,81488% Коэффициент эластичности рассчитаем по формуле (3): 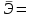 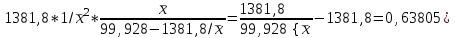 % %Построим график функции с помощью MS Excel. 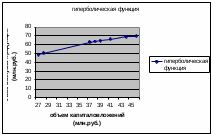 Рис. 5 График гиперболического уравнения регрессии. 9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать выводы. Коэффициенты были рассчитаны в задании 8. Для сравнения моделей составим сводную таблицу 11: Таблица11. Сводная таблица характеристик моделей.
Для всех моделей средняя относительная ошибка аппроксимации не превышает 7%, значит, качество всех моделей хорошее. Коэффициент детерминации более приближен к 1 у гиперболической модели, таким образом, эту модель можно взять в качестве лучшей для построения прогноза. Для гиперболической модели степень связи между факторным и результативным признаком самая низкая, т.к. 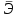 имеет наименьшее значение, а для показательной модели самая высокая, т.к. коэффициент эластичности наибольший. имеет наименьшее значение, а для показательной модели самая высокая, т.к. коэффициент эластичности наибольший.1 2 |