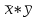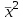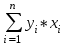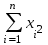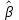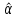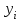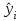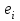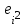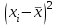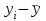Эконометрика. Контрольная работа по дисциплине Эконометрика
 Скачать 331.35 Kb. Скачать 331.35 Kb.
|
1 2 Федеральное агентство по образованию Всероссийский заочный финансово-экономический институт Кафедра экономико-математических методов и моделей КОНТРОЛЬНАЯ РАБОТА по дисциплине «Эконометрика» Вариант № 3 Исполнитель: Глушакова Т.И. Специальность: Финансы и кредит Курс: 3 Группа: 6 № зачетной книжки: 07ффд41853 Руководитель: Денисов В.П. г. Омск 2009г. Задачи По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (X, млн. руб.). Требуется: 1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии. 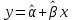 - уравнение линейной регрессии, где - уравнение линейной регрессии, где 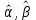 - параметры уравнения. - параметры уравнения.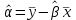 , где , где 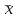 , ,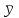 - средние значения признаков. - средние значения признаков.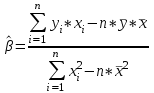 , где n – число наблюдений. , где n – число наблюдений.Представим вычисления в таблице 1: Таблица 1. Промежуточные расчеты.
Таким образом, уравнение линейной регрессии имеет вид: 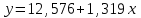 Коэффициент регрессии равен 1,319>0, значит связь между объемом капиталовложений и выпуском продукции прямая, увеличение объема капиталовложений на 1 млн. руб. ведет к увеличению объема выпуска продукции в среднем на 1,319 млн. руб. Это свидетельствует об эффективности работы предприятий. 2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 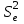 ; построить график остатков. ; построить график остатков.Вычислим прогнозное значение Y по формуле: 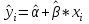 Остатки вычисляются по формуле: 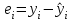 . .Представим промежуточные вычисления в таблице 2. Таблица 2. Вычисление остатков.
Дисперсия остатков вычисляется по формуле: 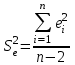 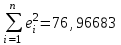  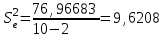 . .Построим график остатков с помощью MS Excel. 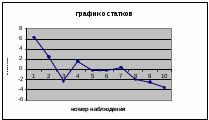 Рис. 1. График остатков. 3. Проверить выполнение предпосылок МНК Проверим независимость остатков с помощью критерия Дарбина-Уотсона. Вычислим коэффициент Дарбина-Уотсона по формуле: 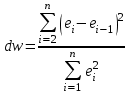 . .Данные для расчета возьмем из таблицы 2. dw = 0,803 Сравним полученное значение коэффициента Дарбина-Уотсона с табличными значениями границ 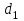 и и 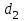 для уровня значимости 0,05 при k=1 и n=10. для уровня значимости 0,05 при k=1 и n=10. 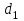 =0,88, =0,88, 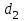 =1,32, dw < d =1,32, dw < d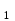 , значит, остатки содержат автокорреляцию. Наличие автокорреляции нарушает одну из предпосылок нормальной линейной модели регрессии. , значит, остатки содержат автокорреляцию. Наличие автокорреляции нарушает одну из предпосылок нормальной линейной модели регрессии.Проверим наличие гетероскедастичности. Т.к. у нас малый объем выборки (n=10) используем метод Голдфельда-Квандта. - упорядочим значения n наблюдений по мере возрастания переменной x и разделим на две группы с малыми и большими значениями фактора x соответственно. - рассчитаем остаточную сумму квадратов для каждой группы. Вычисления представим в таблицах 3 и 4. Таблица 3. Промежуточные вычисления для 1-го уравнения регрессии.
Таблица 4. Промежуточные вычисления для 2-го уравнения регрессии.
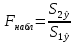 = = 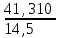 = = 2,849 2,849 где 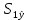 - остаточная сумма квадратов 1-ой регрессии, - остаточная сумма квадратов 1-ой регрессии, 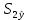 - остаточная сумма квадратов 2-ой регрессии. - остаточная сумма квадратов 2-ой регрессии.Полученное значение сравним с табличным значением F распределения для уровня значимости 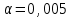 , со степенями свободы , со степенями свободы 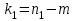 и и 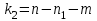 ( (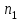 - число наблюдений в первой группе, m – число оцениваемых параметров в уравнении регрессии). - число наблюдений в первой группе, m – число оцениваемых параметров в уравнении регрессии).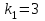 , , 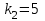 , m=1. , m=1.Если 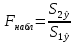 > > 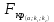 , то имеет место гетероскедастичность. , то имеет место гетероскедастичность.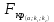 = 5,41 = 5,41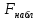 < < 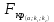 , , значит, гетероскедастичность отсутствует и предпосылка о том, что дисперсия остаточных величин постоянна для всех наблюдений выполняется. 4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента 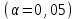 . .Расчетные значения t-критерия можно вычислить по формулам: 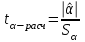 , , 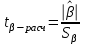 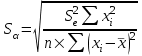 , , 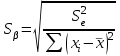 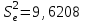 , ,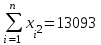 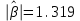 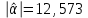 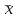 =35,5 =35,5Промежуточные расчеты представим в таблице: Таблица 5. Промежуточные вычисления для расчета t- критерия
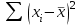 =490,50 =490,50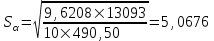 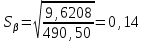 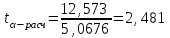 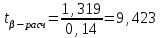 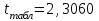 для уровня значимости 0,05 и числа степеней свободы n-2=8 для уровня значимости 0,05 и числа степеней свободы n-2=8Так как 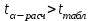 и и 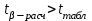 можно сделать вывод, что оба коэффициента регрессии значимые. можно сделать вывод, что оба коэффициента регрессии значимые.5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера 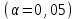 , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели. , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.Коэффициент детерминации определяется по формуле: 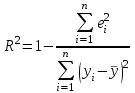 Из расчетов нам известно, что 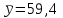 ; ; 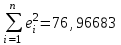 . .Рассчитаем 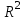 : :Таблица 6. Промежуточные вычисления для расчета коэффициента детерминации.
 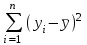 =930,4 =930,4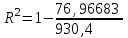 =0,917. =0,917.Т.к. значение коэффициента детерминации близко к единице, качество модели считается высоким. Теперь проверим значимость уравнения регрессии. Рассчитаем значение F-критерия Фишера 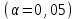 по формуле: по формуле: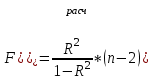 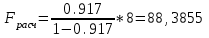 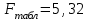 Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. 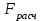 > >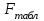 . .Средняя относительная ошибка аппроксимации находится по формуле: 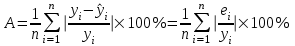 Таблица 7. Промежуточные вычисления для расчета средней относительной ошибки аппроксимации.
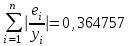 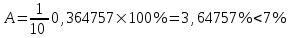 , , значит модель имеет хорошее качество. Рассчитаем коэффициент эластичности по формуле: 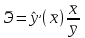 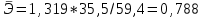 6. осуществить прогнозирование среднего значения показателя Y при уровне значимости 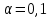 , если прогнозное значение фактора X составит 80% от его максимального значения. , если прогнозное значение фактора X составит 80% от его максимального значения.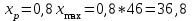 Рассчитаем стандартную ошибку прогноза 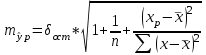 , ,где 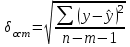 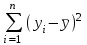 =930,4 ; =930,4 ; 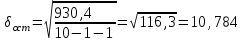 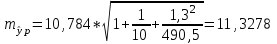 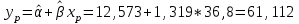 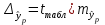 , , 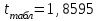 для уровня значимости 0,1 и числа степеней свободы n-2=8 для уровня значимости 0,1 и числа степеней свободы n-2=8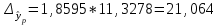 Доверительный интервал прогноза: 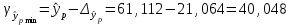 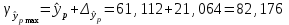 Таким образом, 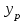 =61,112 , будет находиться между верхней границей, равной 82,176 и нижней границей, равной 40,048. =61,112 , будет находиться между верхней границей, равной 82,176 и нижней границей, равной 40,048. 1 2 |