ГИДРОГАЗОДИНАМИКА. Контрольная работа по дисциплине Гидрогазодинамика
 Скачать 329.05 Kb. Скачать 329.05 Kb.
|
|
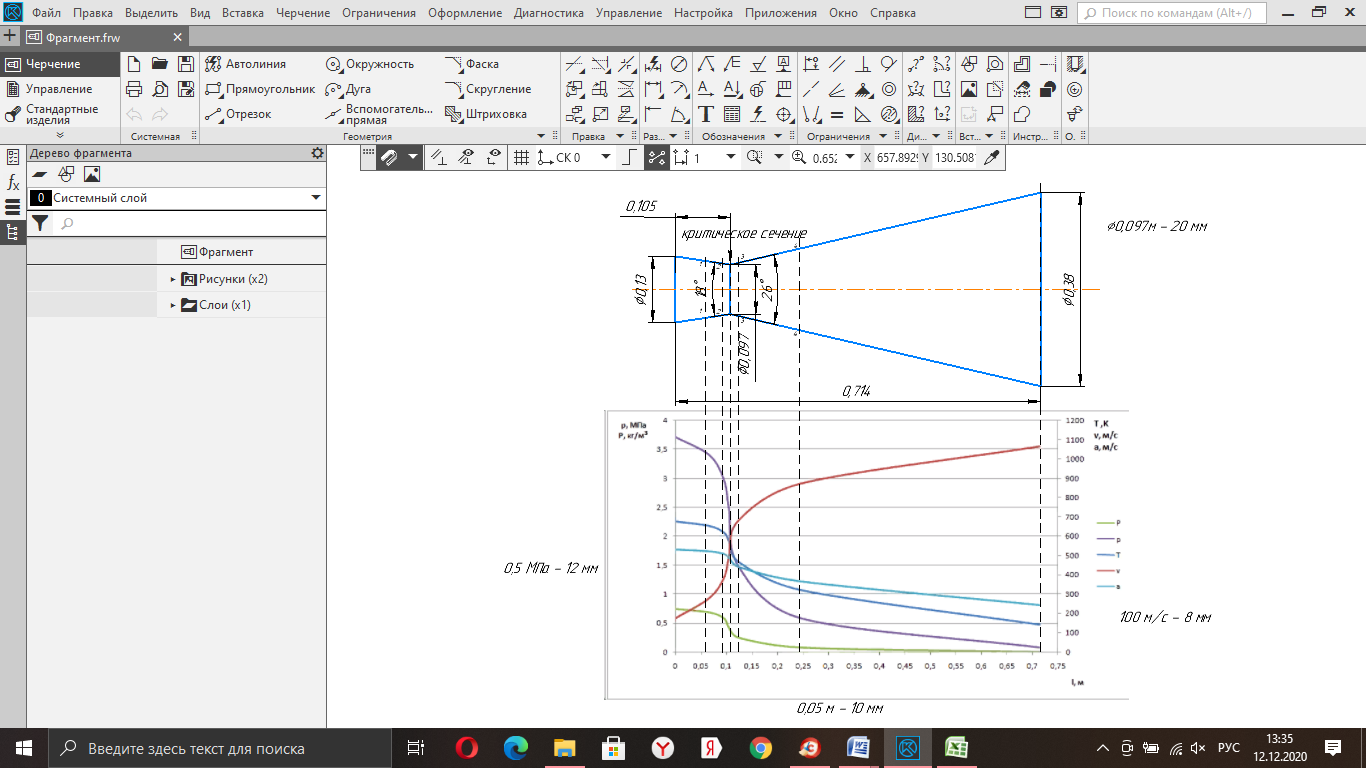
Таблица 2 Основные физические свойства газов 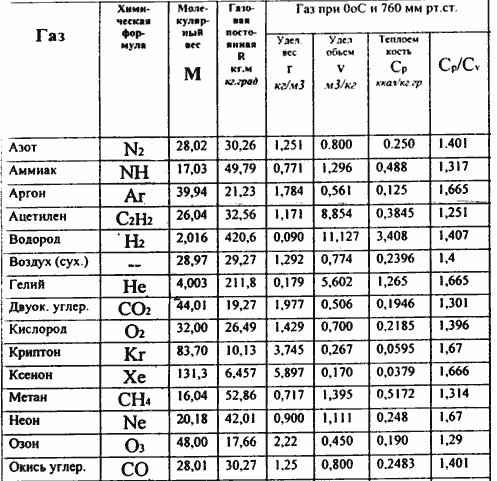  Определить: Необходимо провести газодинамический расчёт сопла Лаваля, обеспечивающего на расчётном режиме заданный расход газа. Для этого нужно провести расчёт параметров газа во входном, в критическом, в выходном и в дополнительных сечениях (1,2,3,4), определить профиль сопла и обобщить полученные результаты. Решение. Из таблицы 2 выберем недостающие термодинамические параметры для углекислого газа. В последующем расчете примем, что термодинамические параметры — удельная изобарная теплоёмкость газа 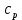 и показатель адиабаты и показатель адиабаты 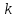 остаются неизменными в процессе расширения. остаются неизменными в процессе расширения. Теплофизические свойства 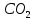 : :— молекулярная масса углекислого газа 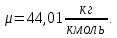 — газовая постоянная углекислого газа 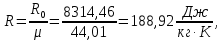 где 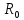 – универсальная газовая постоянная – универсальная газовая постоянная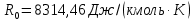 . .— показатель адиабаты углекислого газа при н.у. 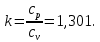 — удельная изобарная теплоёмкость углекислого газа 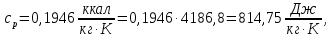 Расчёт параметров газа в критическом сечении. Из уравнения Менделеева-Клапейрона находим плотность углекислого газа при полной остановке потока (плотность торможения): 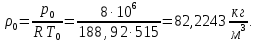 Скорость звука в заторможенном потоке: 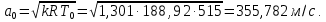 Скорость звука в критическом сечении: 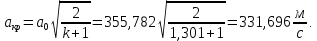 Скорость потока углекислого газа в критическом сечении: в критическом сечении число Маха 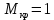 и коэффициент скорости и коэффициент скорости 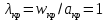 , откуда , откуда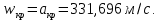 Температура, давление и плотность углекислого газа в критическом сечении: 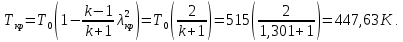 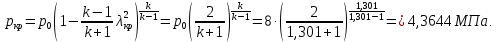 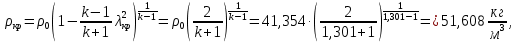 или, для проверки: 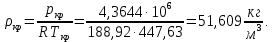 Из уравнения неразрывности потока находим площадь критического сечения: 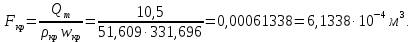 Диаметр критического сечения: 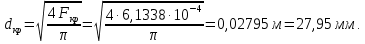 Расчёт параметров газа во входном сечении сопла Лаваля Коэффициент скорости во входном сечении: 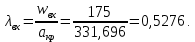 Термические параметры углекислого газа на входе в сопло: — температура углекислого газа 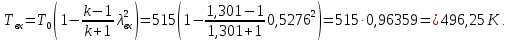 — давление углекислого газа 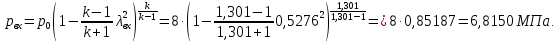 — плотность углекислого газа 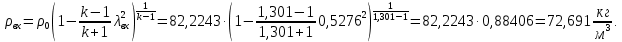 Площадь входного сечения (из уравнения неразрывности): 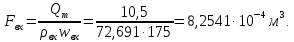 Диаметр входного сечения: 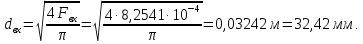 Скорость звука во входном сечении: 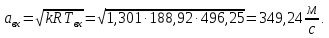 Число Маха во входном сечении: 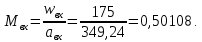 Расчёт параметров потока в выходном сечении Расчетным режимом сопла называется случай, когда статическое давление потока на выходе из сопла 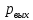 равно внешнему атмосферному давлению равно внешнему атмосферному давлению 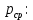 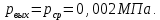 В этом случае коэффициент скорости 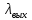 в выходном сечении сопла Лаваля находится по формуле в выходном сечении сопла Лаваля находится по формуле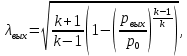 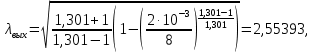 Термические параметры углекислого газа на выходе из сопла: — температура углекислого газа 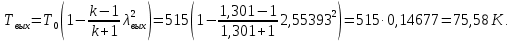 — плотность углекислого газа 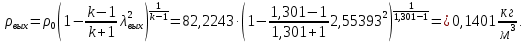 Скорость углекислого газа на выходе из сопла 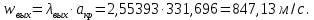 Скорость звука на выходе из сопла 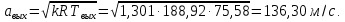 Число Маха на выходе из сопла: 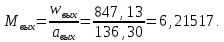 Площадь выходного сечения (из уравнения неразрывности): 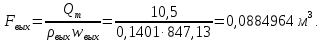 Диаметр входного сечения: 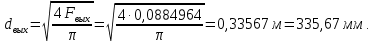 Геометрический профиль сопла. Длина суживающейся (дозвуковой) части сопла находится по формуле, связывающей катеты прямоугольного треугольника: 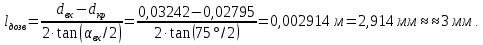 Т.о., получился очень короткий дозвуковой участок сопла Лаваля. Длина расширяющейся (сверхзвуковой) части сопла: 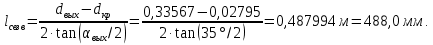 Общая длина сопла Лаваля: 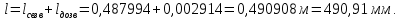 Геометрический профиль расчётного конического сопла Лаваля изображен на рис. 2. и 3. На рис. 3 масштаб по длине сопла увеличен в 100 раз из-за разных порядков длин дозвуковой и сверхзвуковой частей сопла. Расчет дополнительных промежуточных сечений. Методика расчета основных параметров потока углекислого газа в дополнительных промежуточных сечениях выполняется аналогично пункту 3 данной записки. Проиллюстрируем расчет для одного сечения, для остальных сечений представим окончательные результаты в Таблице 3. Зададимся безразмерным коэффициентом скорости, величина которого больше 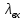 и меньше и меньше 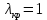 , например, , например,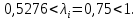 Определим скорость углекислого газа в 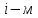 сечении сечении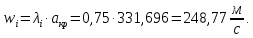 Найдем термические параметры углекислого газа в этом сечении: — температура углекислого газа 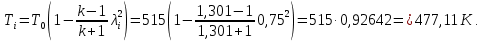 — давление углекислого газа 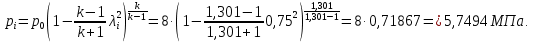 — плотность углекислого газа 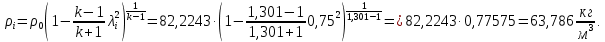 Площадь  сечения (из уравнения неразрывности): сечения (из уравнения неразрывности):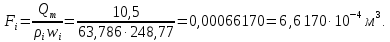 Диаметр 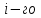 сечения: сечения: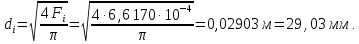 Скорость звука в 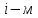 сечении: сечении: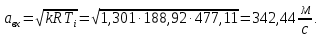 Число Маха в  сечении: сечении: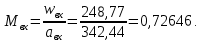 Положение  сечения: расстояние от входа в сопло до сечения: расстояние от входа в сопло до 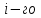 сечения (координату сечения (координату 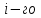 сечения) найдем из соотношения катетов прямоугольного треугольника: сечения) найдем из соотношения катетов прямоугольного треугольника: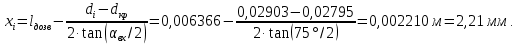 Для сечений, расположенных за критическим сечением, определение координаты сечения будет отличаться формулой: 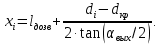 Расчеты проделаем для 2-х промежуточных сечений в дозвуковой части сопла для 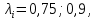 и 2-х промежуточных сечений в сверхзвуковой части сопла: 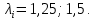 Результаты расчетов представлены в Таблице 3 и на графиках (см. рис. 4-8). По данным таблицы 3 построены графики изменения основных параметров потока (T, р, ρ, w, a, λ, M) по длине сопла, а также диаметра сопла d (рис. 4‒8). Дозвуковая и свкрхзвуковая часть сопла и изменение параметров потока вдоль неё показана в разном масштабе (масштаб для дозвуковой части взят в 100 раз больше, чем для сверхзвуковой) в силу отличного порядка геометрических размеров. Выводы: 1). Расчет сопла Лаваля был произведен для нормального режима работы, поскольку давление на срезе сопла было принято равным давлению окружающей среды и отсутствовали скачки уплотнения в сверхзвуковой части сопла, что обеспечило сверхзвуковую скорость на выходе из сопла равную 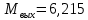 . .2). Характер изменения параметров потока вдоль оси сопла Лаваля существенно нелинейный, в области критического сечения наблюдаются максимальные градиенты всех параметров потока. 3). Сопло высотное, поэтому геометрические размеры сверхзвуковой части намного превосходят его дозвуковую часть. 4). Углекислый газ — тяжелый газ, с относительно невысоким показателем адиабаты k, а, значит, с низкой сжимаемостью. Если бы вместо него в сопле расширялся водород  ( (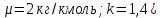 или гелий или гелий 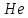 ( (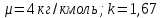 ), при таком же перепаде давлений и температуре торможения удалось бы получить гораздо большие скорости истечения на срезе сопла. ), при таком же перепаде давлений и температуре торможения удалось бы получить гораздо большие скорости истечения на срезе сопла.Таблица 3. Результаты газодинамического расчета сопла Лаваля
 |