Контрольная работа по компюторной практике. Черненко КР по компьюторному практикуму. Контрольная работа по дисциплине Компьютерный практикум вариант 2 Выполнила студентка Черненко А. В форма обучения очная
 Скачать 126.01 Kb. Скачать 126.01 Kb.
|
|
Федеральное государственное образовательное бюджетное учреждение высшего образования «Финансовый университете при Правительстве Российской Федерации» (Тульский филиал Финуниверситета) Кафедра «Математика-информатика» Контрольная работа по дисциплине «Компьютерный практикум» вариант 2 Выполнила студентка: Черненко А. В Форма обучения: очная Курс: 1 Направление подготовки: экономика Профиль: финансы и кредит Личное дело №: 100.26/180185 Проверил преподаватель: к.ф-м.н., доц. Васина М.В. Тула – 2018 г. Задание 1. Провести с помощью MSExcel полное численное исследование функции F(x)= 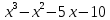 с построением графика и нахождением нулей функции, точек локальных экстремумов и перегибов. 1. Общая характеристика функции. 1.1 Область определения функции. Функция определяется для любых значений аргумента х, поэтому ее область определения ( 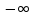 ; ; 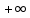 ) )1.2 Поведение функции в окрестностях точек разрыва. Данная функция не имеет точек разрыва. 1.3 Точки пересечения графика с осями координат. Ось Ох: при у = 0 нужно решить уравнение: 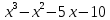 =0 =0Получили одна точка пересечения (1; 0). Ось Оу: при х = 0. Подставим это значение в уравнение функции: F(0)= 0-0+0-10=-10 (0;-10) 1.4 Симметрия графика. Определим четность функции: F(-x)= 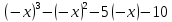 = = 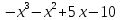 = =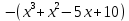 ≠ -F(x) ≠ F(x). ≠ -F(x) ≠ F(x).Следовательно, функция не является ни четной, ни нечетной. 1.5 Периодичность графика. Степенные функции не периодичны. 2. Интервалы монотонности и экстремумы функции. 2.1 Вычисление первой производной функции. F(x)’= 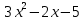 2.2 Определение критических точек. Соответственно: F(x)’= 0 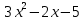 =0, отсюда =0, отсюда 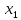 =7/3, =7/3, 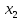 =-2/3 =-2/32.3 Нахождение интервалов монотонности. Рассмотрим поведение производной функции на трех полученных промежутках: От - ∞ до -2/3 F(-2)’= 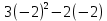 -5 > 0 – функция возрастающая. -5 > 0 – функция возрастающая.От -2/3 до 7/3 F(0)’= 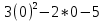 < 0 – функция убывающая. < 0 – функция убывающая.От 7/3 до +∞ F(2)= 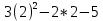 > 0 – функция возрастающая. > 0 – функция возрастающая.2.4 Определение экстремумов функции. Получаем в точке – (-2/3) точку максимума, а в точке – 7/3 точку минимума. Найдём координаты этих точек. F(-2/3) = -200/27=-7,40740741 F(7/3) = 389/27=14,4074074 3. Интервалы выпуклости и вогнутости. 3.1 Вычисление второй производной функции. F(x)’= 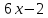 3.2 Определение точек перегиба. Вычислим точку перегиба. Соответственно: x= 1/3 – точка перегиба. 3.3 Нахождение интервалов выпуклости и вогнутости. Рассмотрим знак 2-й производной на промежутках: От -∞ до 1/3 F(-2)’’= 6(-2)-2 < 0 – функция выпукла вверх. От 1/3 до + ∞ F(2) = 6(2)-2 > 0 – функция выпукла вниз. Найдём координату точки перегиба: F(1/3) = 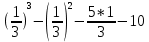 =-317/27=11,7407407 =-317/27=11,74074074. Наклонные асимптоты графика функции. Наклонных асимптот не существует. 5. График функции. 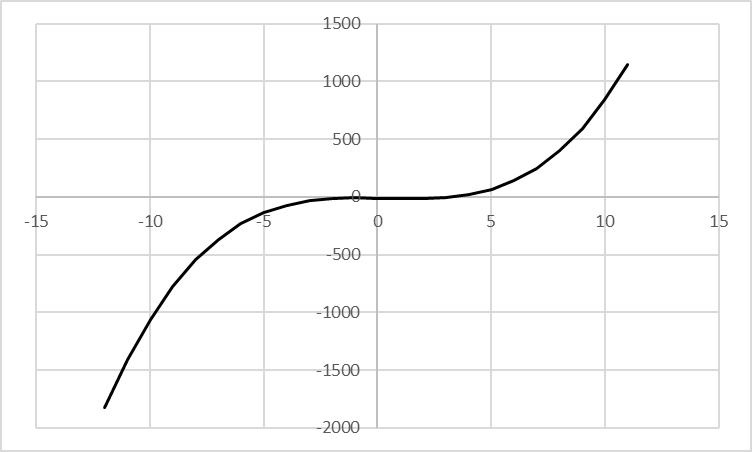 Задание 2. Вычислить с помощью R в точке 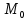 (1,2,1) значение функции (1,2,1) значение функции 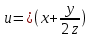 , а так же её градиент и гессиан. , а так же её градиент и гессиан.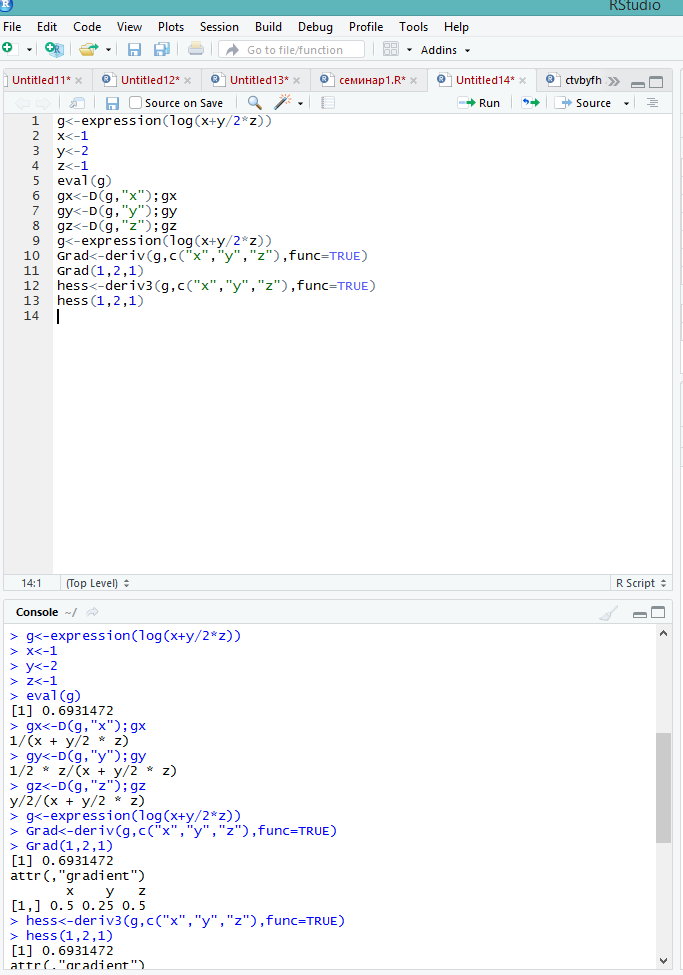 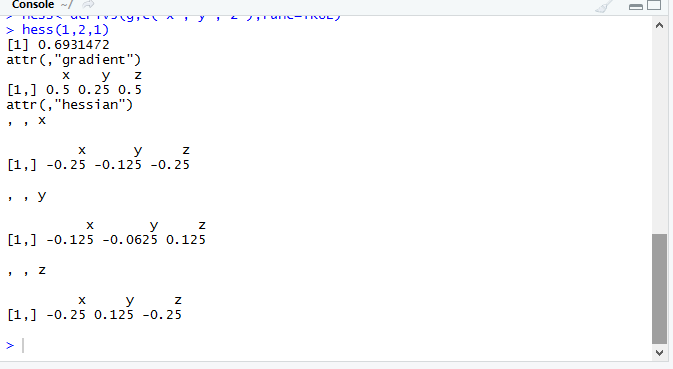 Задание 3. Вычислить с помощью R интегралы 3.1 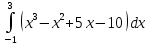 3.2 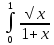 3.1 Первое, что нам требуется сделать, – это объявить в R подынтегральную функцию . 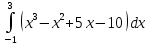 с помощью кода: f <-function(x) {х^3-x^2+5x-10} # Объявление функции f(x)=x^3-x^2+5x-10 После данного шага нажать «Run», чтобы функция была обработана компилятором R. Далее нам требуется вызвать специальную базовую процедуру численного интегрирования в R по правилу: integrate(f, -1, 3) 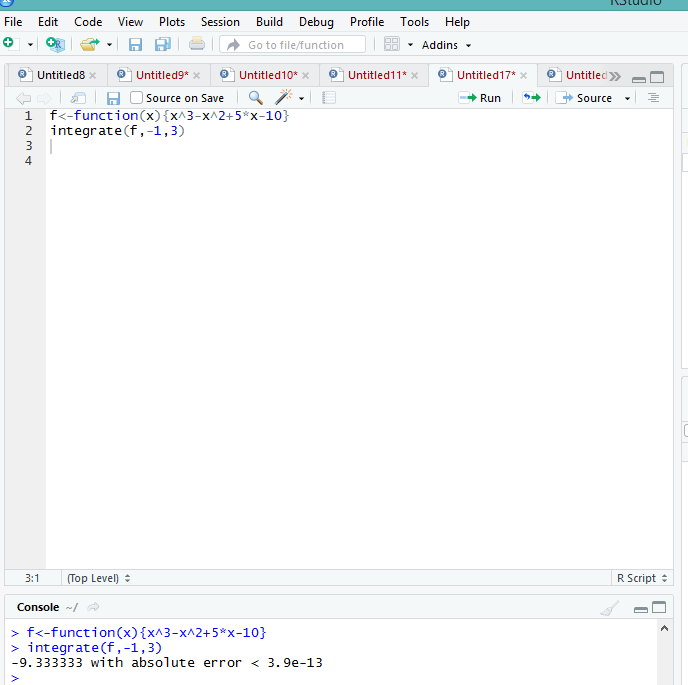 3.2 Объявляем в R подынтегральную функцию . 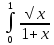 с помощью кода: h<-function(x) {(x^0.5)/(1+x} # Объявление функции h(x)=(x^0.5)/(1+x) После данного шага нажать «Run», чтобы функция была обработана компилятором R. Далее нам требуется вызвать специальную базовую процедуру численного интегрирования в R по правилу: integrate(h, 0, 1)$value # Приближенное значение интеграла … 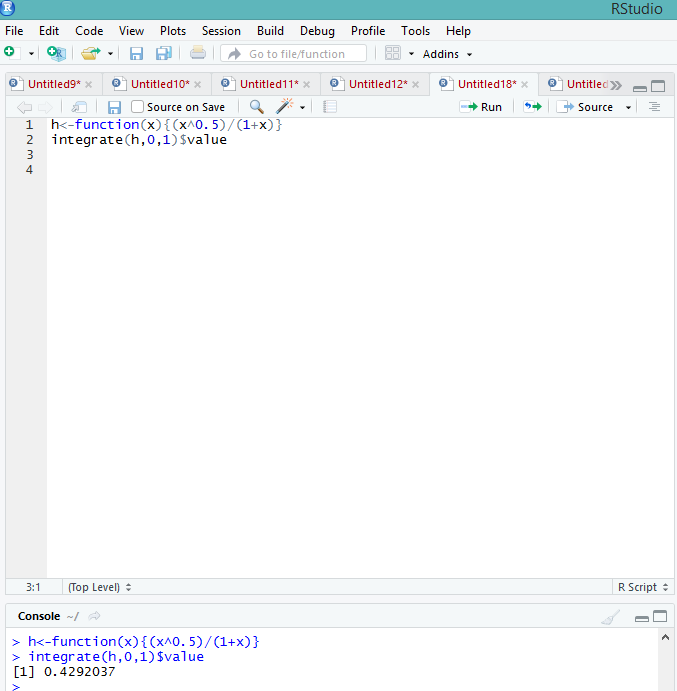 |
