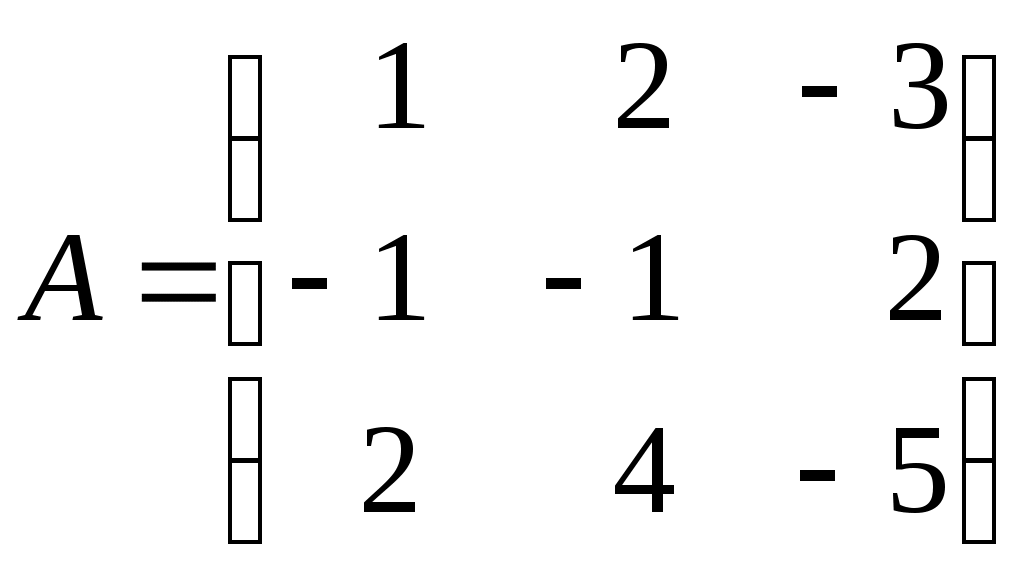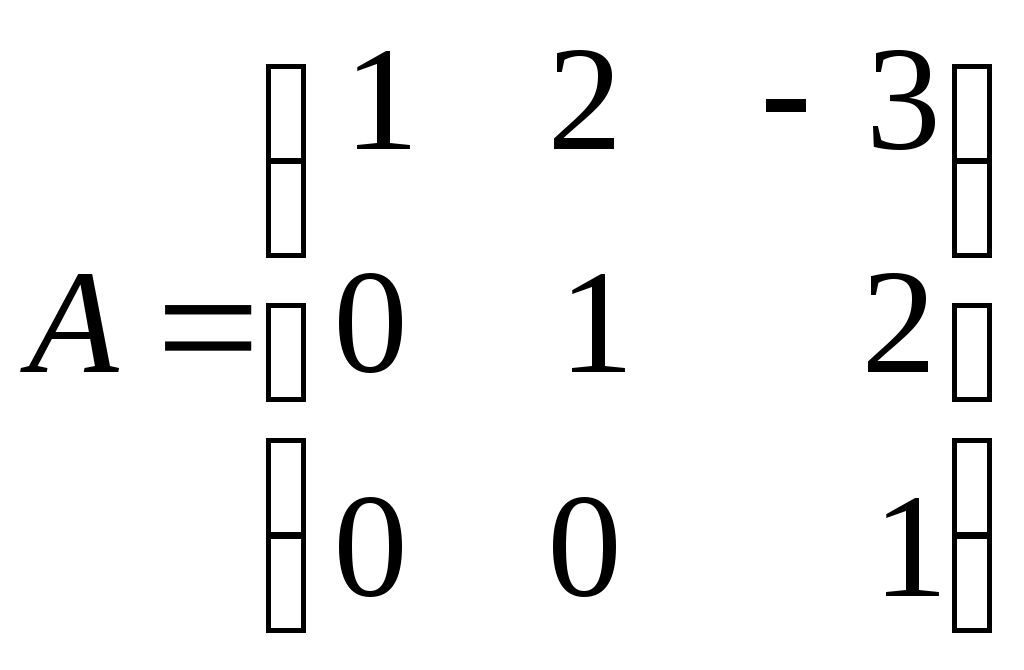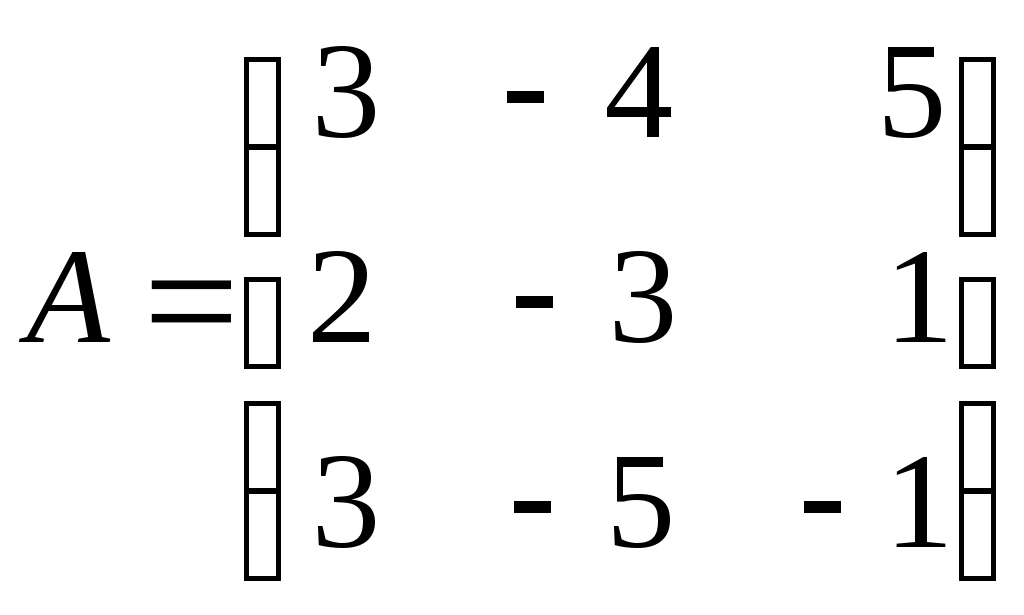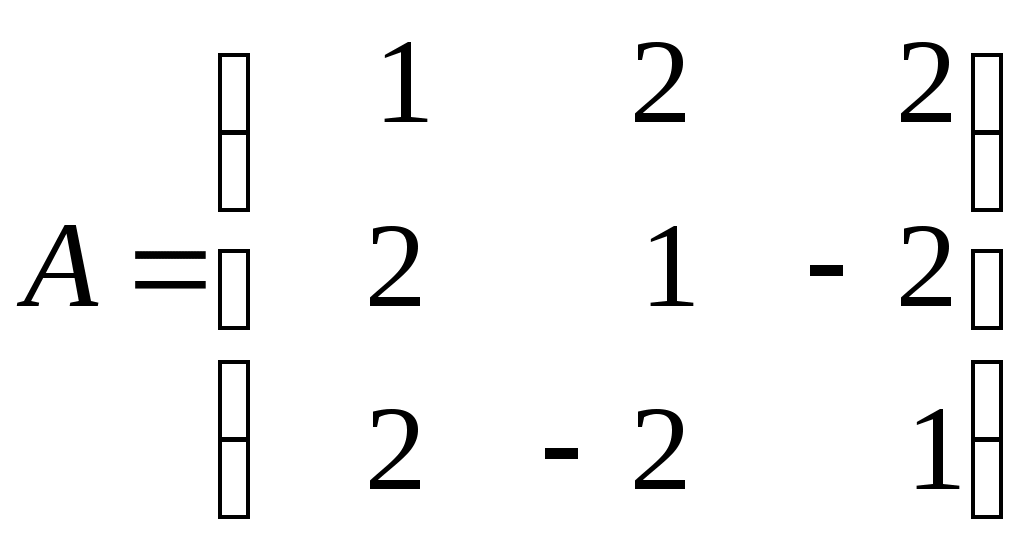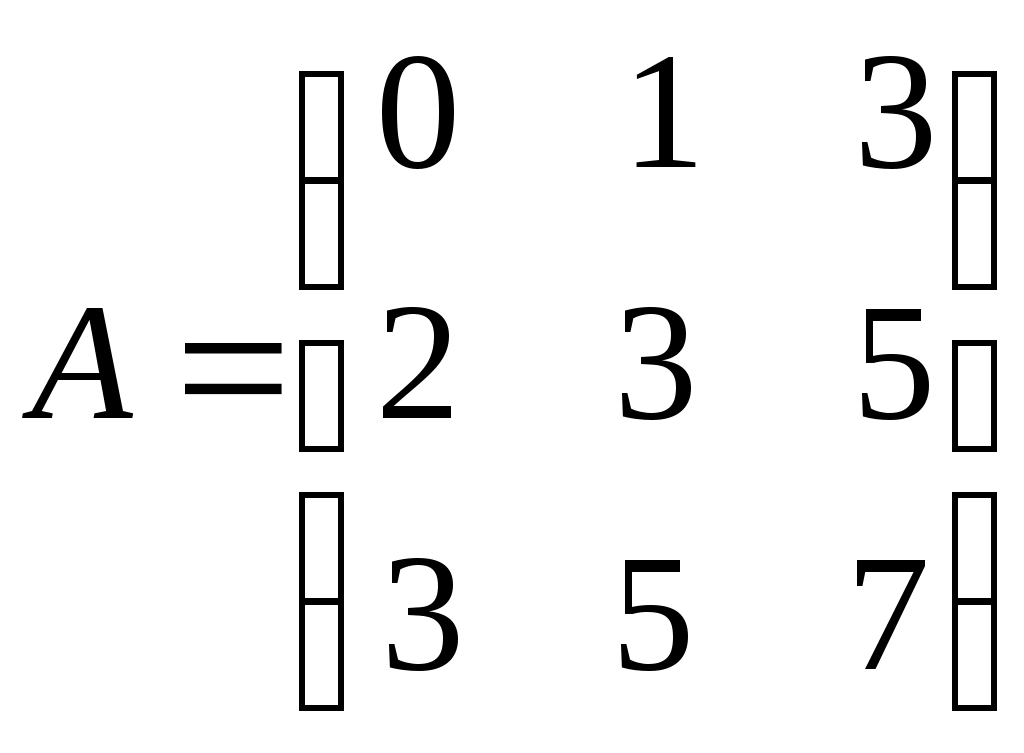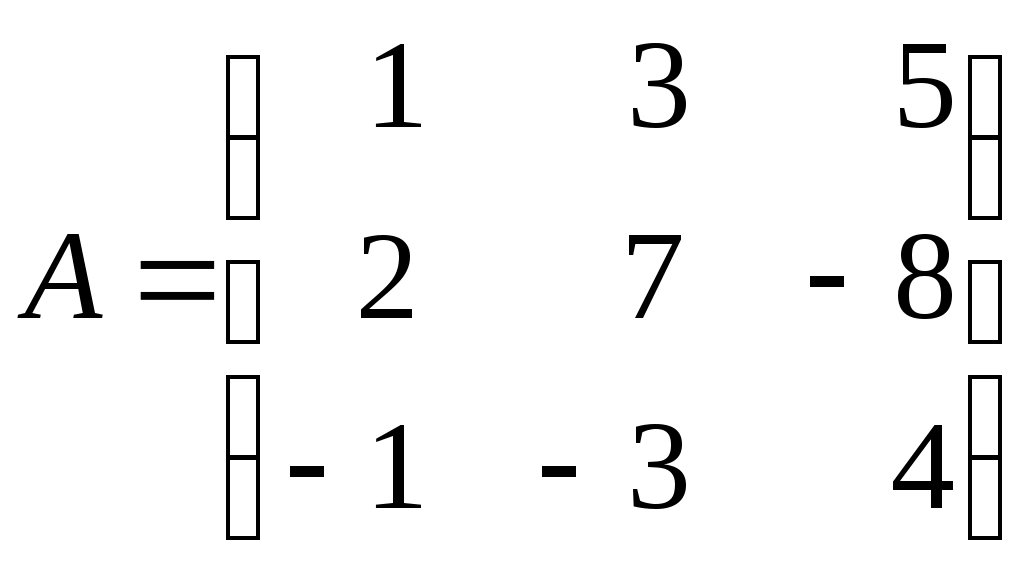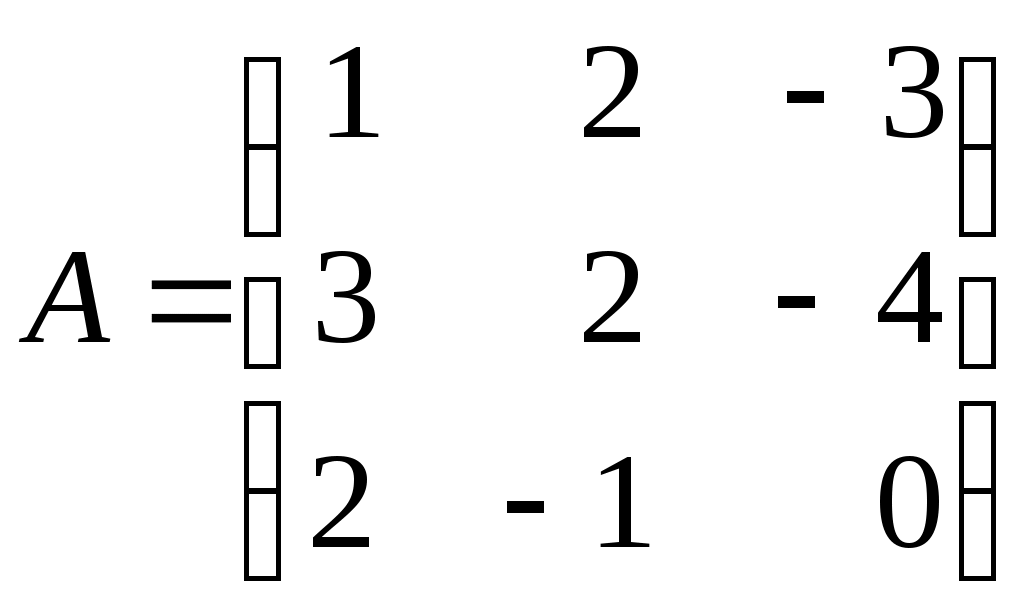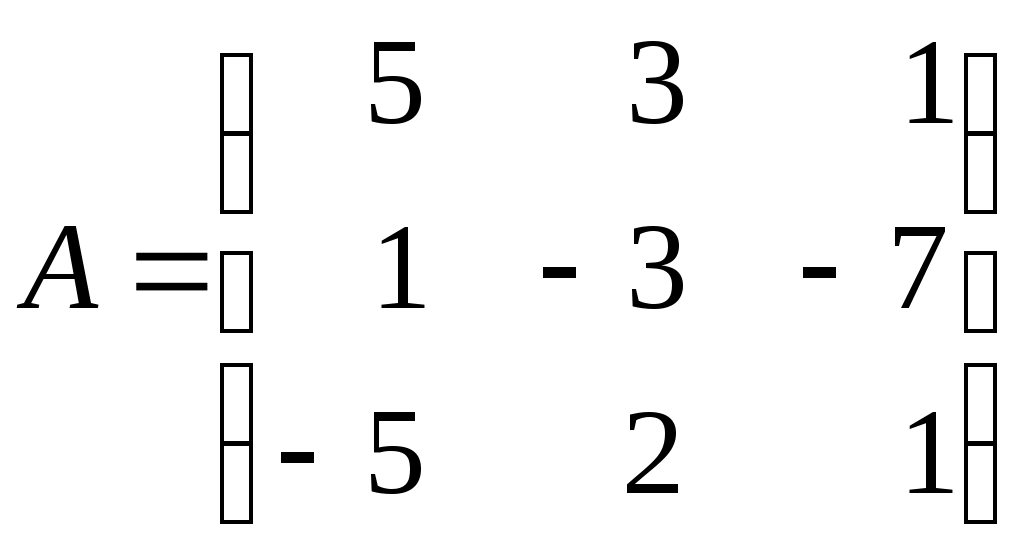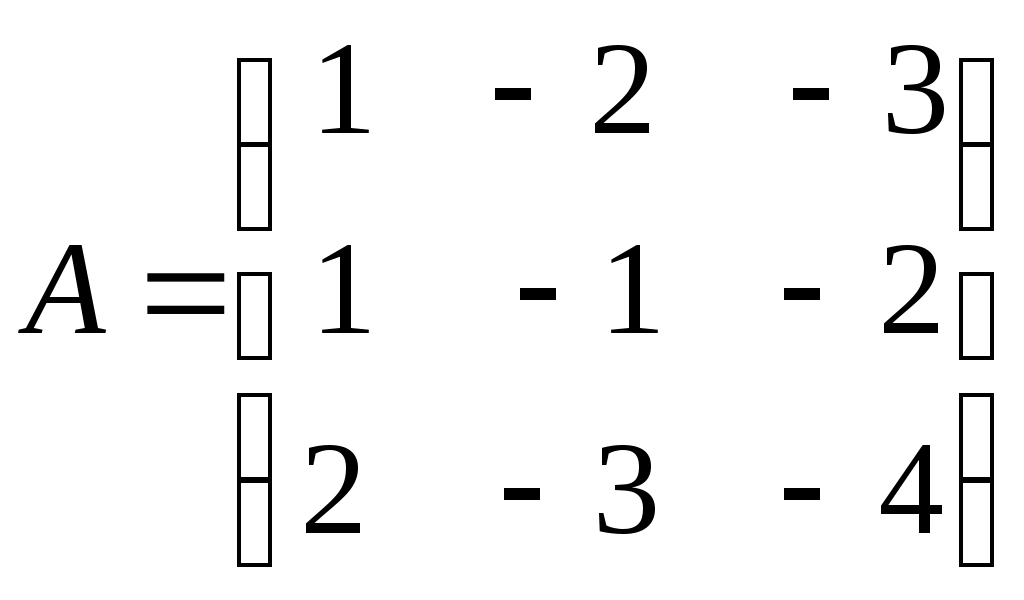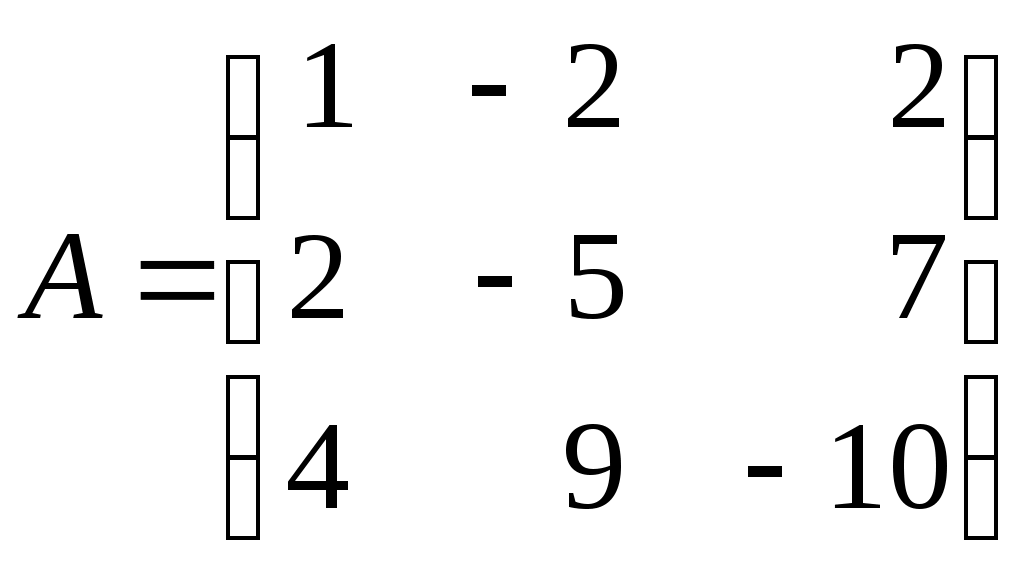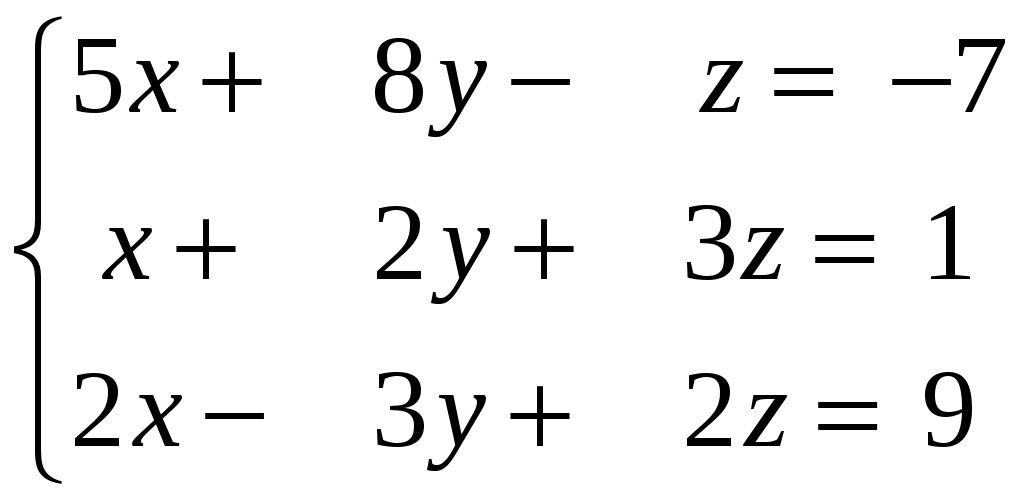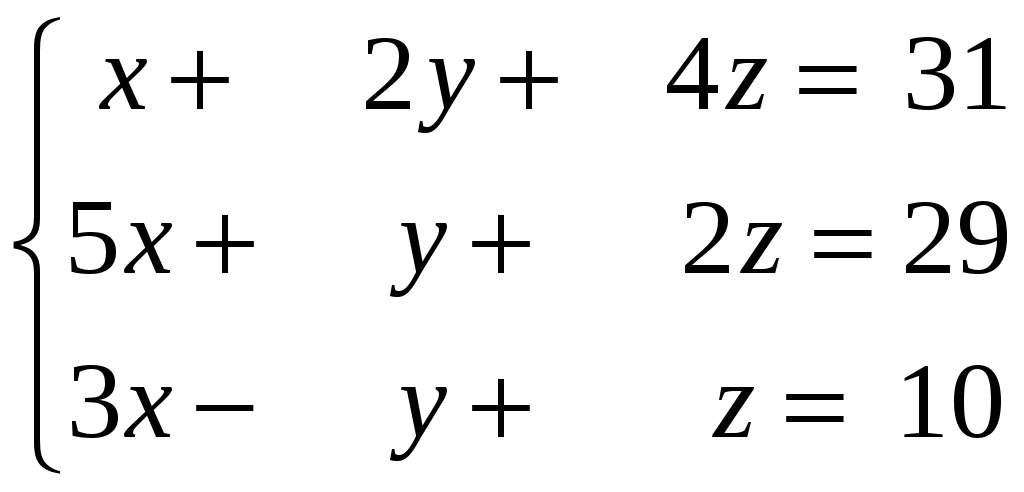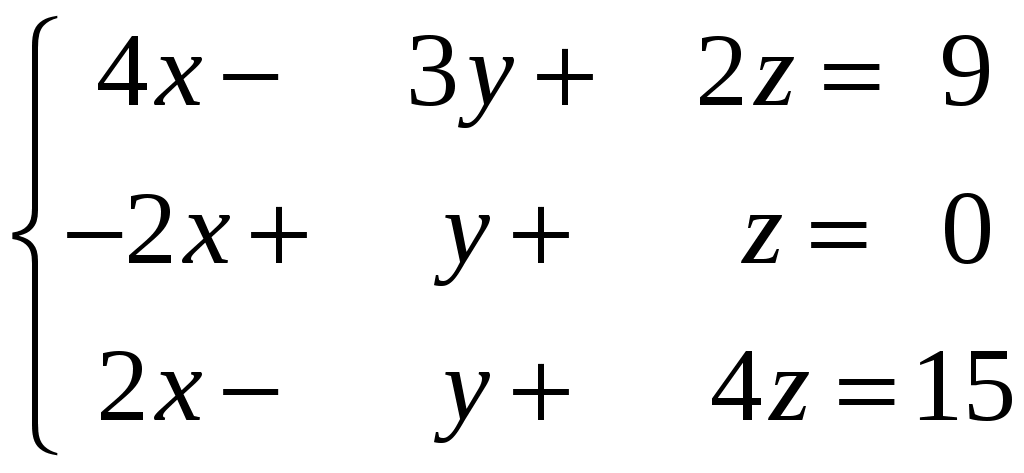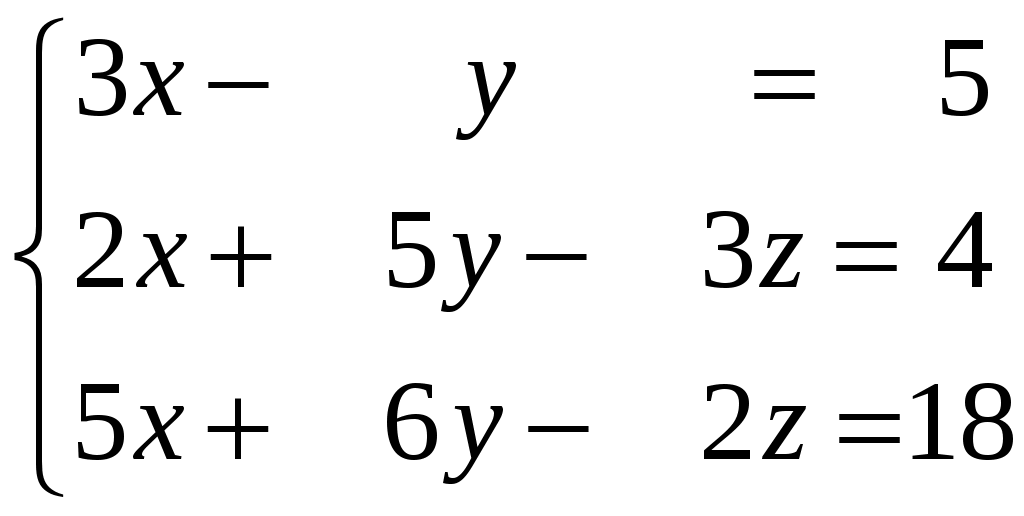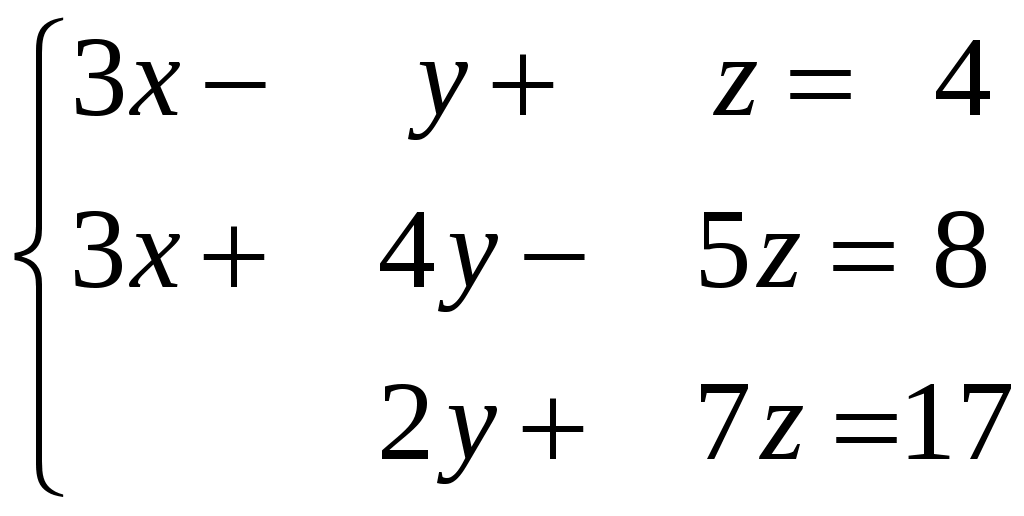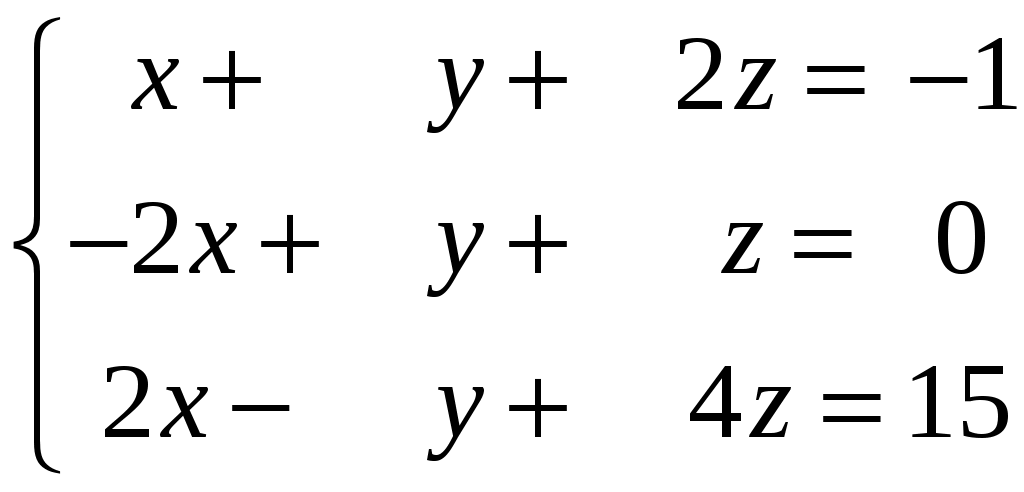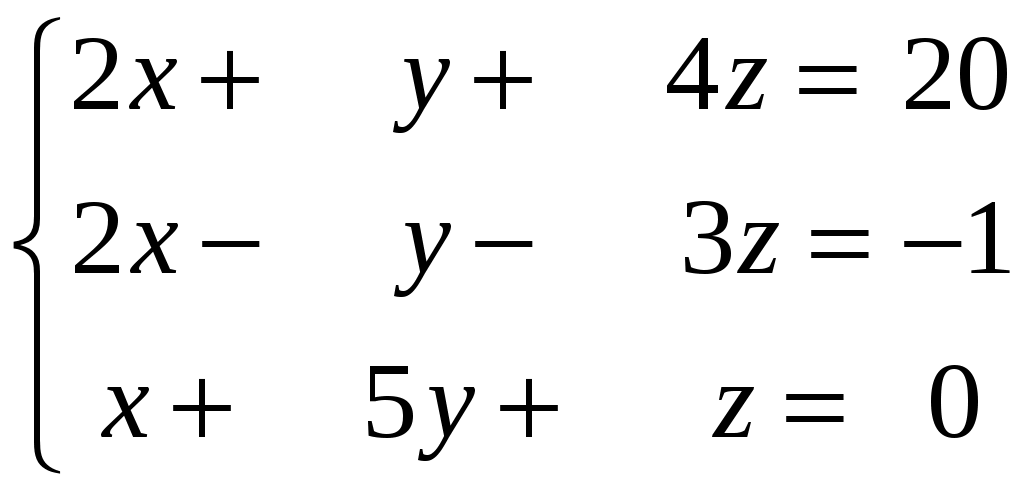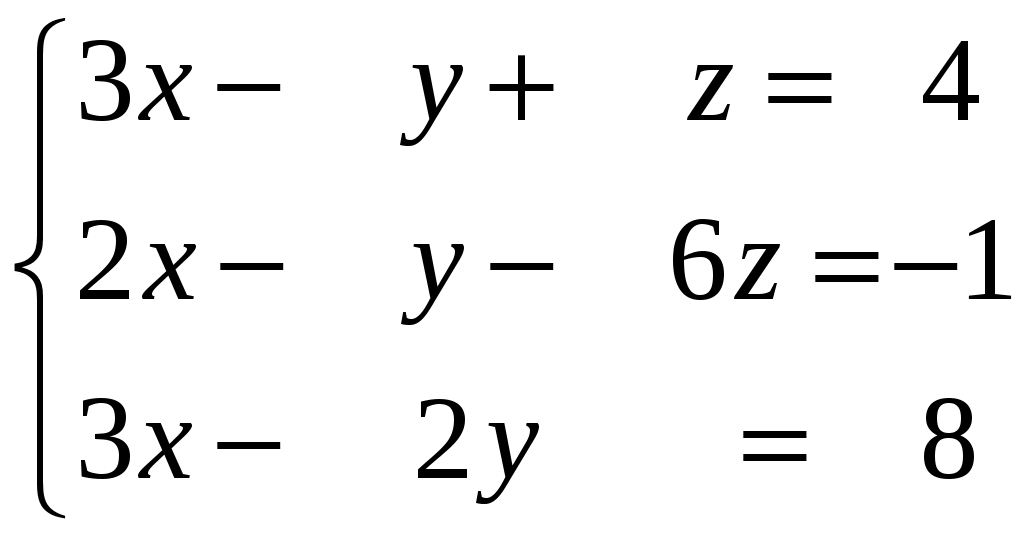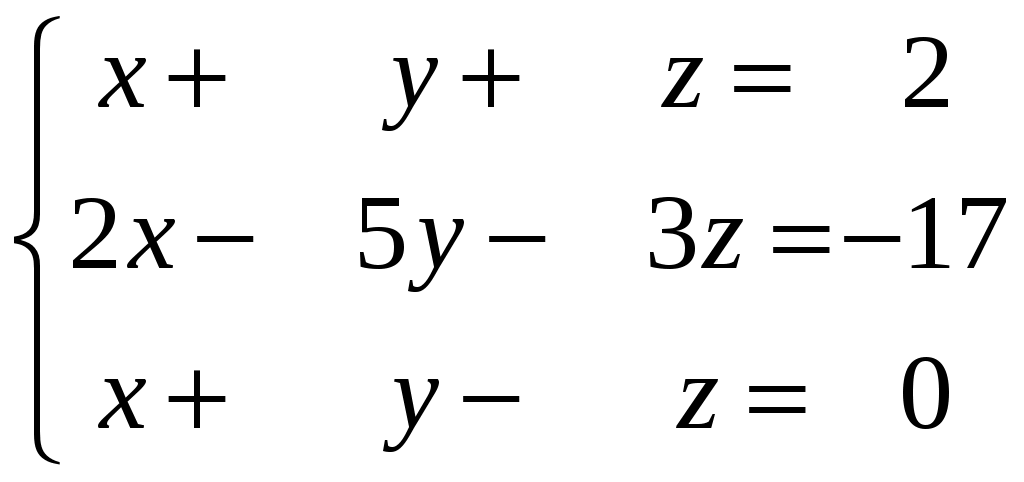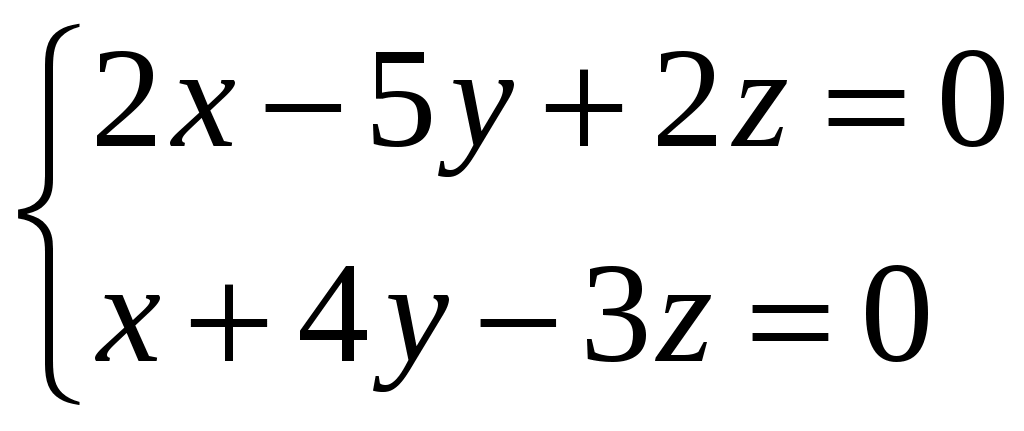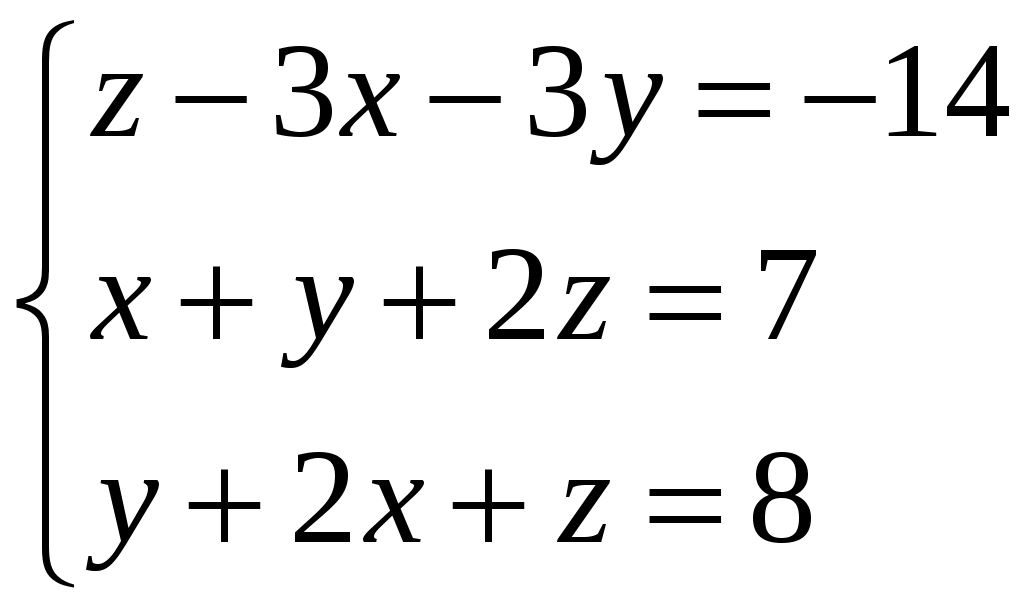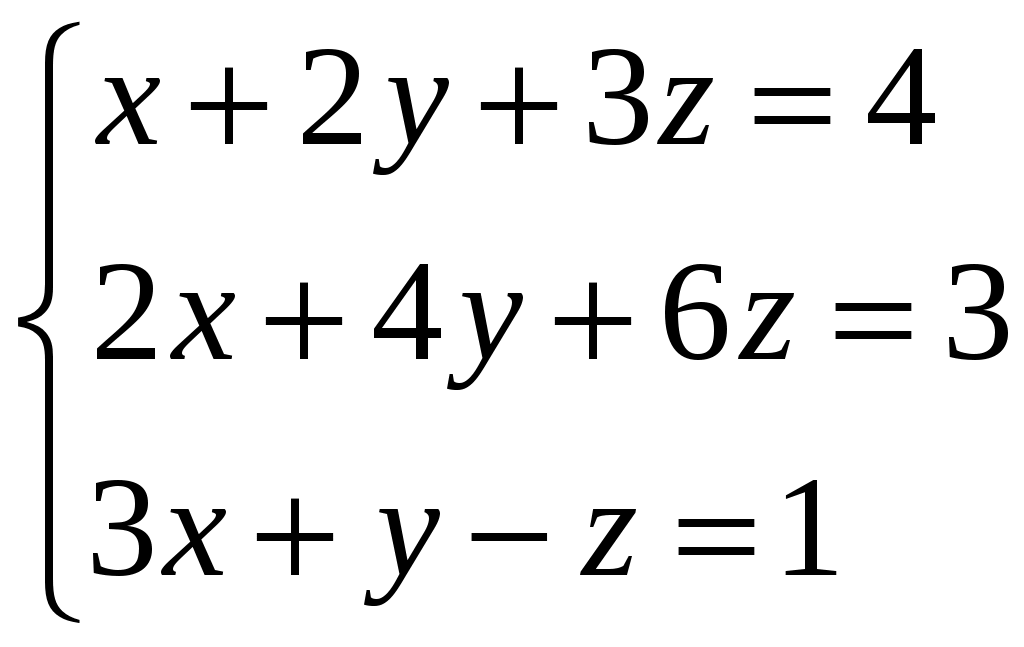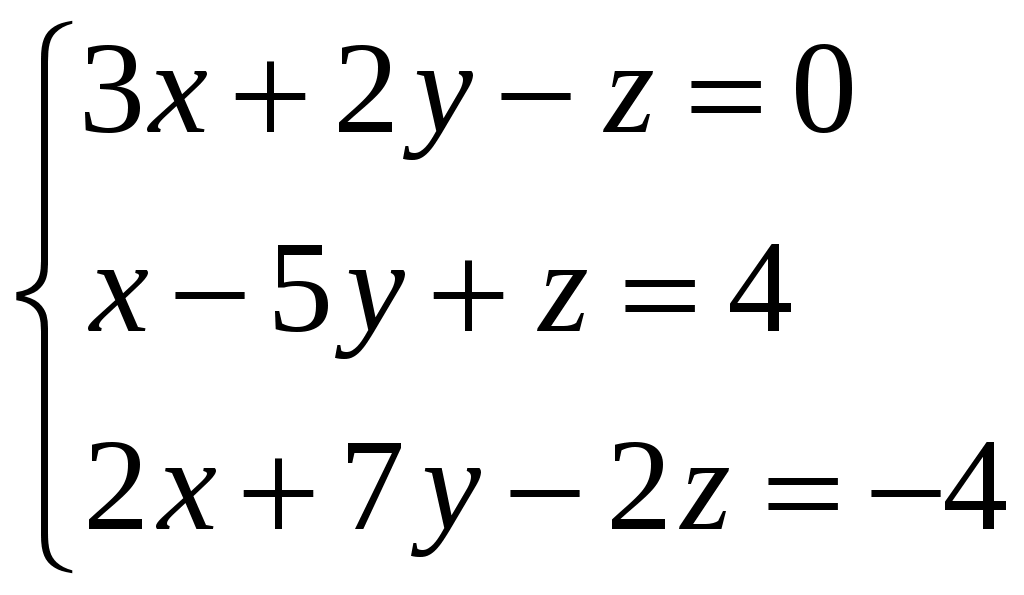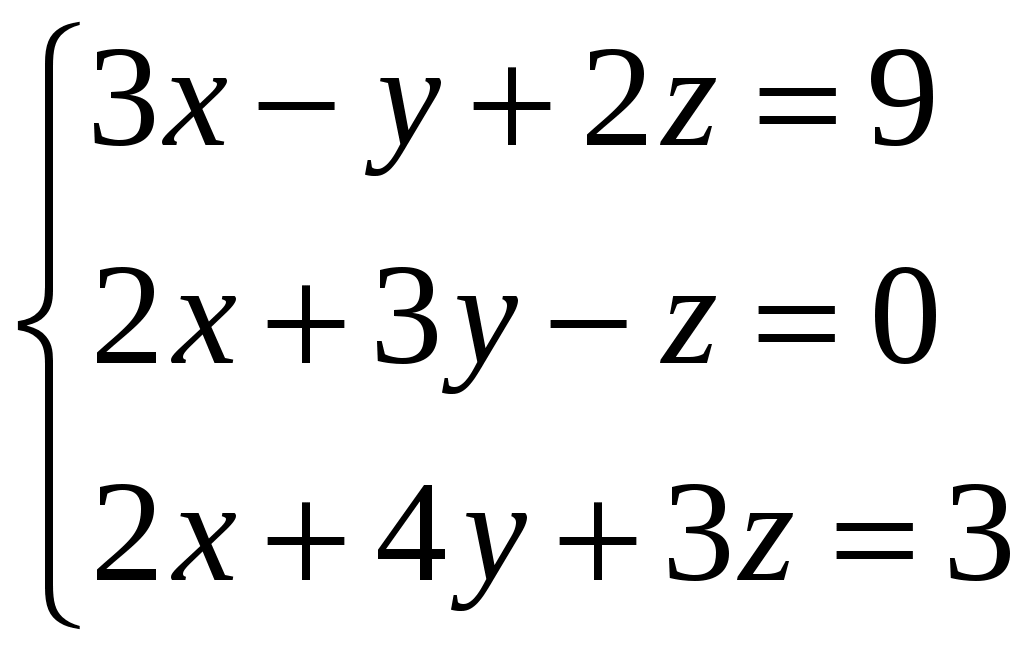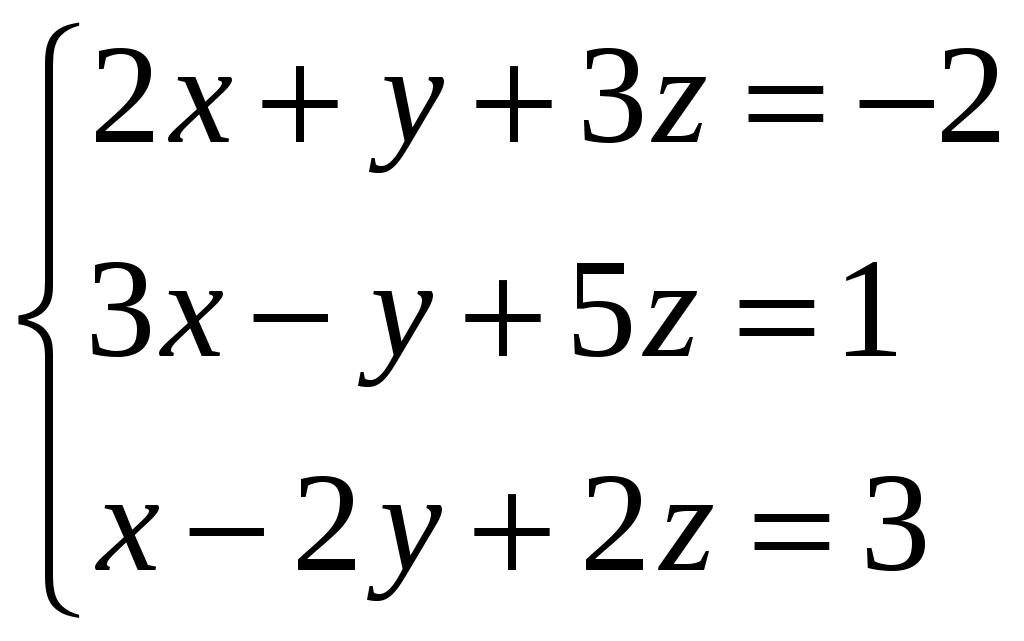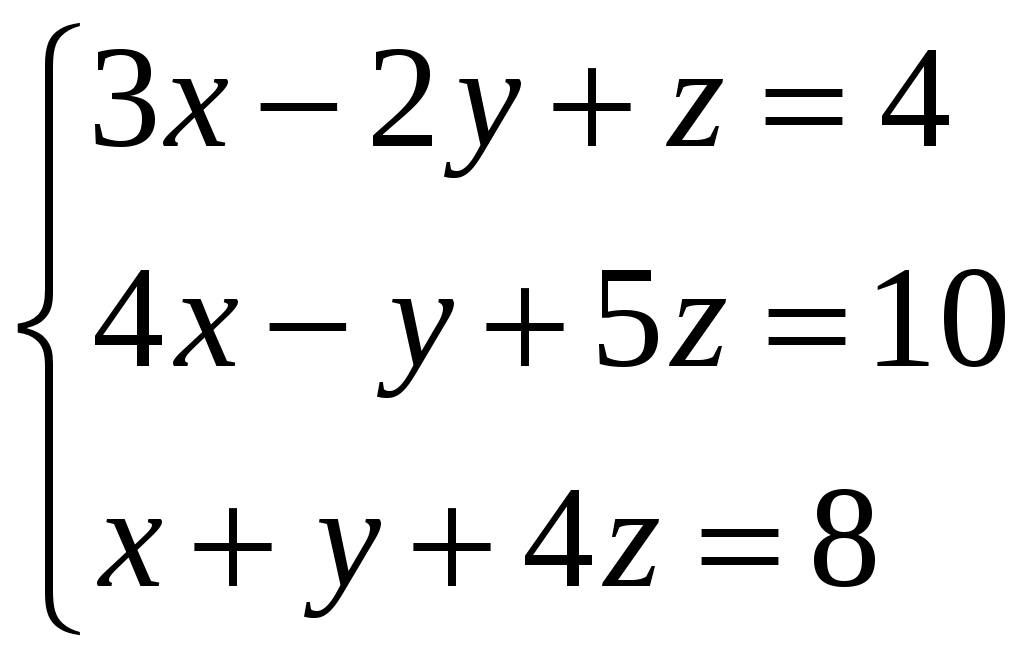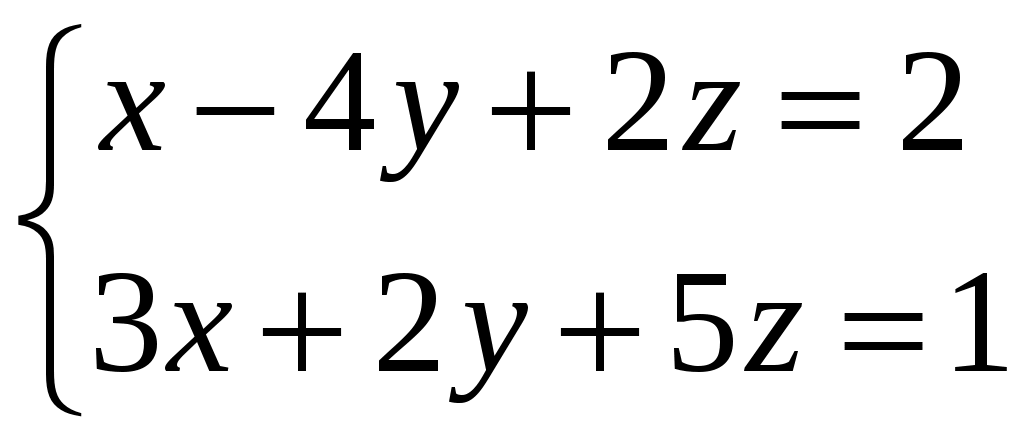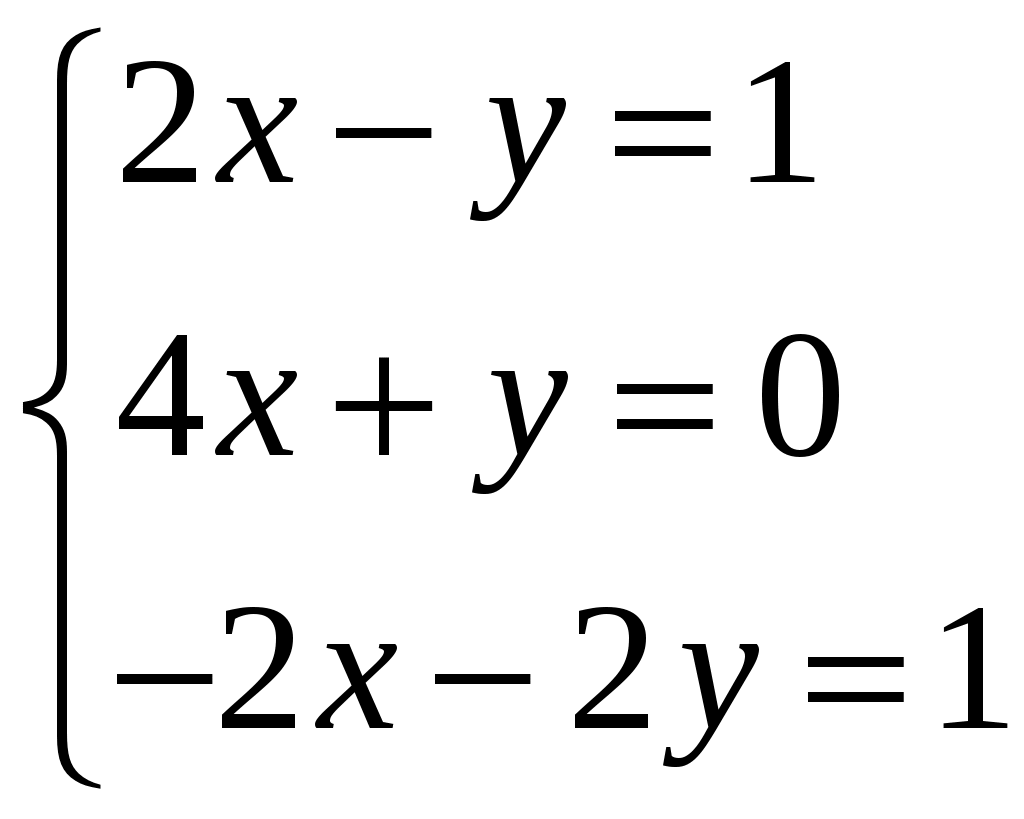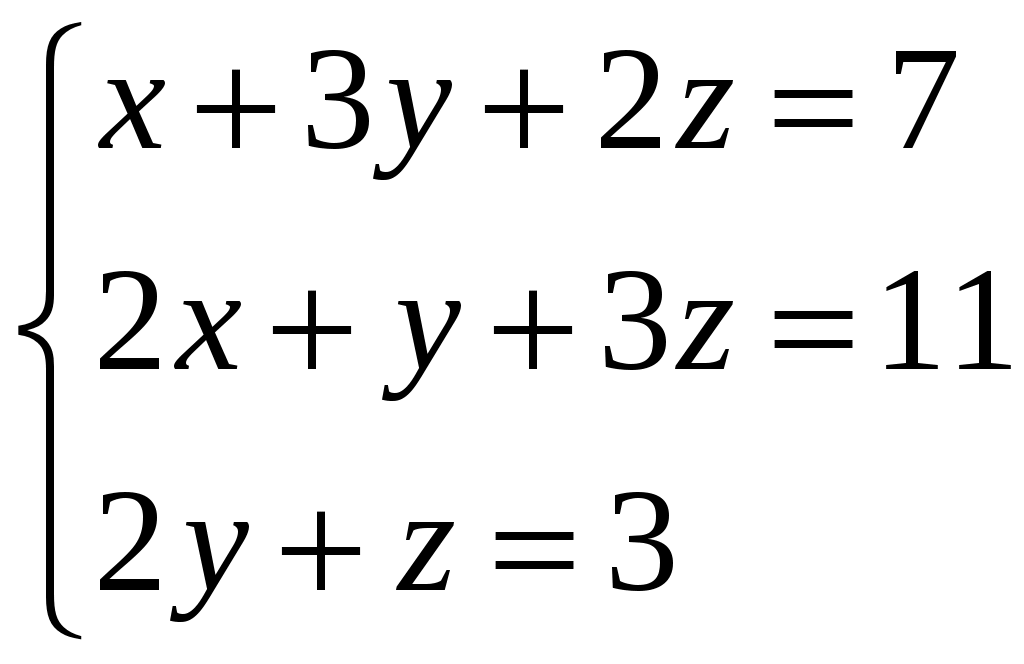Линейная алгебра контрольная. ЛинАлгАнГеом_ИАТМ_КонРаб. Контрольная работа по дисциплине Линейная алгебра и аналитическая геометрия

• Название: Контрольная работа по дисциплине Линейная алгебра и аналитическая геометрия
• Анкор: Линейная алгебра контрольная
• Дата: 11.01.2023
• Размер: 264 Kb.
• Имя файла: ЛинАлгАнГеом_ИАТМ_КонРаб.doc
• Тип: Контрольная работа; #880996

Контрольная работа по дисциплине

«Линейная алгебра и аналитическая геометрия»

для студентов ИАТМ

(1 семестр, заочное отделение)

Методические указания по выполнению контрольной работы

.

В соответствии с учебным планом студенты заочного отделения ИАТМ выполняют задания контрольной работы по дисциплине «Линейная алгебра и аналитическая геометрия». Каждый студент выполняет один вариант контрольной работы. Выбор варианта осуществляется по последней цифре в номере зачётной книжки, причем, если номер зачетки оканчивается на 0, то студент выполняет 10-й вариант.
Выполняя контрольную работу, студент должен руководствоваться следующим:

1. 
   Контрольную работу необходимо сдавать в сроки, установленные графиком учебного процесса (как минимум за 3 дня до даты экзамена (зачета)).
   
2. 
   Контрольную работу следует выполнять в отдельной тетради, указав на титульном листе свои ФИО, группу, факультет, ФИО лектора кафедры математики.
   
3. 
   К экзамену (зачету) студент допускается только с зачтенной контрольной работой.
   

Вопросы для подготовки к экзамену (зачету)

1. 
   Матрицы и действия над ними.
   
2. 
   Обратная матрица.
   
3. 
   Определители и их свойства.
   
4. 
   Решение систем линейных уравнений методами Крамера и Гаусса.
   
5. 
   Векторы и действия над ними.
   
6. 
   Скалярное произведение векторов и его свойства.
   
7. 
   Линейная зависимость и независимость векторов.
   
8. 
   Разложение вектора по базисным векторам.
   
9. 
   Уравнения прямой на плоскости (общее, каноническое, проходящей через две точки, параметрическое, с угловым коэффициентом).
   

Рекомендуемая литература

1. 
   Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М., 1995.
   
2. 
   Щипачев В.С. Высшая математика. М., 2001.
   
3. 
   Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. – 2-е изд., - М.: Айрис-пресс, 2004.
   

Задания контрольной работы
Задание 1.

Найти: а) обратную матрицу . Проверить равенство ;

б) матрицу , где получается из ее транспонированием

Вариант	Матрица	Вариант	Матрица
1.		2.
3.		4.
5.		6.
7.		8.
9.		10.

Задание 2. Решить системы уравнений: а) по правилу Крамера;

б) матричным способом.

вариант	Исходные данные
1
2
3
4
5
6
7
8
9
10

Задание 3.

Решить системы методом Гаусса. Записать общее решение системы и два частных решения (если есть).

Вариант	Система	Вариант	Система
1.		2.
3.		4.
5.		6.
7.		8.
9.		10.

Задание 4.

Коллинеарны ли вектора и ?

вариант
1	1	-2	3	3	0	-1	2	4	-1	3
2	1	0	1	-2	3	5	1	2	3	-1
3	-2	4	1	1	-2	7	5	3	2	-1
4	1	2	-3	2	-1	-1	4	3	8	-1
5	3	5	4	5	9	7	-2	1	3	-2
6	1	4	-2	1	1	-1	1	1	4	2
7	1	-2	5	3	-1	0	4	-2	-2	1
8	3	4	-1	2	-1	1	6	-3	-2	1
9	-2	-3	-2	1	0	5	3	9	-1	-3
10	-1	4	2	3	-2	6	2	-1	-6	3

Задание 5.

Исследовать на линейную зависимость систему векторов

вариант
1	1	4	6	1	-1	1		1		1	3
2	2	-3	1	3	-1	5		1		-4	3
3	5	4	3	3	3	2		8		1	3
4	1	1	1	0	1	1		0		0	1
5	1	-1	2	-1	1	-1		2		-1	1
6	1	2	3	4	5	6		7		8	9
7	1	1	1	1	2	3		1		3	6
8	3	4	-5	8	7	-2		2		-1	8
9	3	2	-4	4	1	-2		5		2	-3
10	0	1	1	1	0	1		1		1	0

Задание 6.

Написать разложение вектора по векторам .

вариант
1	-2	4	7	0	1	2	1	0	1	-1	2	4
2	6	12	-1	1	3	0	2	-1	1	0	-1	2
3	1	-4	4	2	1	-1	0	3	2	1	-1	1
4	-9	5	5	4	1	1	2	0	-3	-1	2	1
5	-5	-5	5	-2	0	1	1	3	-1	0	4	1
6	13	2	7	5	1	0	2	-1	3	1	0	-1
7	-19	-1	7	0	1	1	-2	0	1	3	1	0
8	3	-3	4	1	0	2	0	1	1	2	-1	4
9	3	3	-1	3	1	0	-1	2	1	-1	0	2
10	-1	7	-4	-1	2	1	2	0	3	1	1	-1

Задание 7. Даны координаты вершин треугольника ABC. Найти: длины сторон треугольника ABC; 2) внутренние углы данного треугольника; 3) длину медианы AE; 4) уравнения сторон AB, BC, CA (общее, каноническое, проходящей через две точки, параметрическое, с угловым коэффициентом). Сделать чертеж.

вариант	Исходные данные
1	A( 4 ; 0 ), B( 7 ; 4 ), C( 8 ; 2 )
2	A( 2 ; 2 ), B( 5 ; 6 ), C( 6 ; 4 )
3	A( 0 ; 2 ), B( 3 ; 6 ), C( 4 ; 4 )
4	A( 4 ; 1 ), B( 7 ; 5 ), C( 8 ; 3 )
5	A( 3 ; 2 ), B( 6 ; 6 ), C( 7 ; 4 )
6	A(-2 ; 1 ), B( 1 ; 5 ), C( 2 ; 3 )
7	A( 4 ; -3), B( 7 ; 1 ), C( 8 ;-1 )
8	A(-2 ; 2 ), B( 1 ; 6 ), C( 2 ; 4 )
9	A( 5 ; 0 ), B( 8 ; 4 ), C( 9 ; 2 )
10	A( 2 ; 3 ), B( 5 ; 7 ), C( 6 ; 5 )