ТУСУР высшая математика, в4. КР 1.4. Контрольная работа по дисциплине Математика. Интегральное исчисление Вариант 1. 4 Студент гр. А. С. Соломатин
 Скачать 225 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра экономики Контрольная работа по дисциплине «Математика. Интегральное исчисление» Вариант №1.4 Студент гр. А.С.Соломатин (подпись) (И. О. Фамилия) «____»____________2020 г. Томск 2020 Найти неопределённые интегралы 1.  ; Из  следует, что  Тогда:  2.  ; Из  следует, что  Тогда:  3.  ;Из  следует, что  Тогда:  4.  ; Из  следует, что  Тогда  5.  ; Используем формулу  Тогда  , значит   , значит  Тогда:  6.  ;Используем формулу Тогда 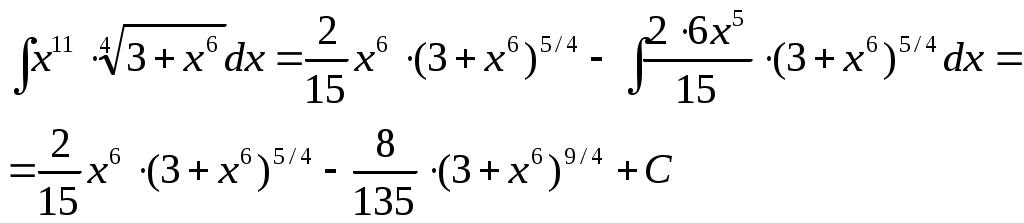 , значит   , значит   Тогда  7.  ; Делаем замену  , тогда 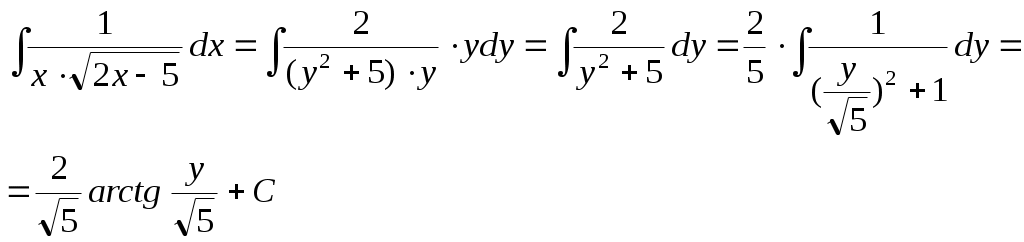 , значит  и  Тогда  Производим обратную замену:  8.  ; Преобразуем:  Для интегрирования рациональных функций вида 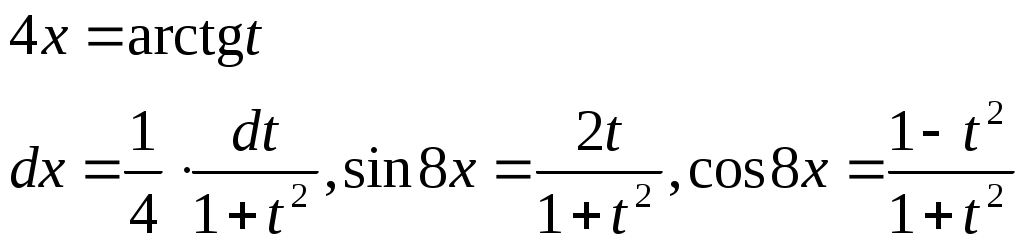 применяем универсальную тригонометрическую подстановку  .  Подставляем в исходный интеграл: 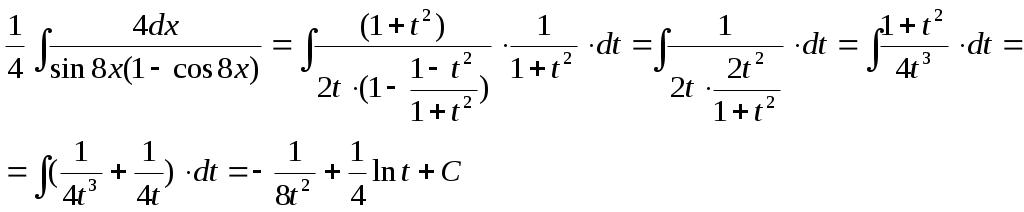 Производим обратную подстановку:  9.  .   Составляем систему: 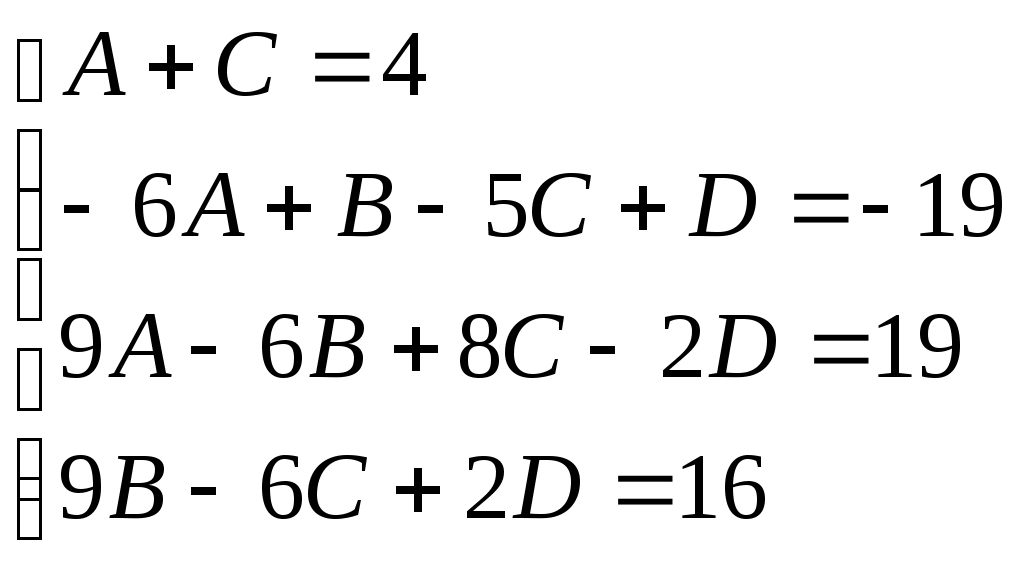 Решение: 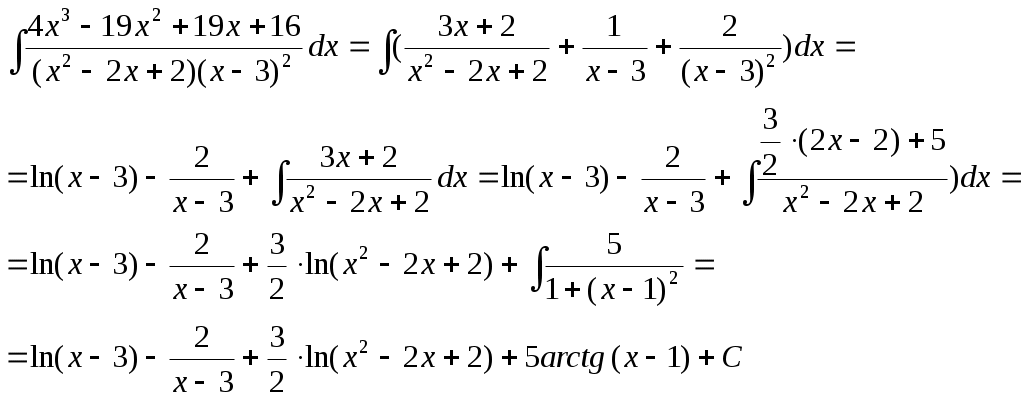   Вычислить определённые интегралы 10.  ; Находим сначала неопределенный интеграл. Используем формулу Тогда  , значи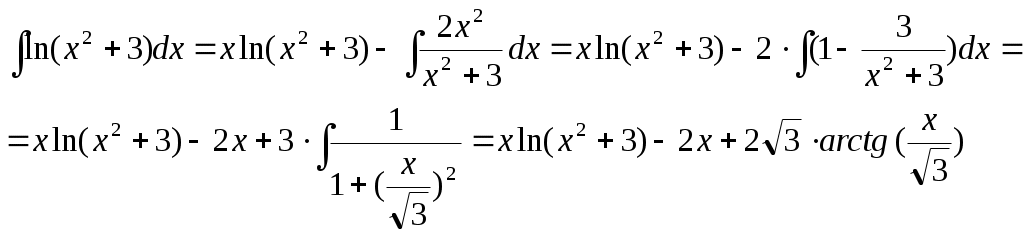т   , значит  Тогда  Теперь находим определенный интеграл: 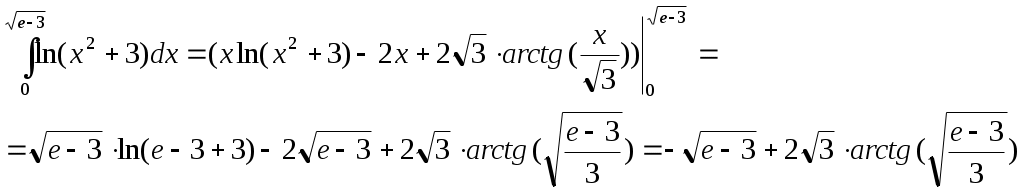 11.  .Сначала находим неопределенный интеграл:  Теперь находим определенный интеграл:  Вычислить несобственные интегралы или установить их расходимость 12.  ; Предел 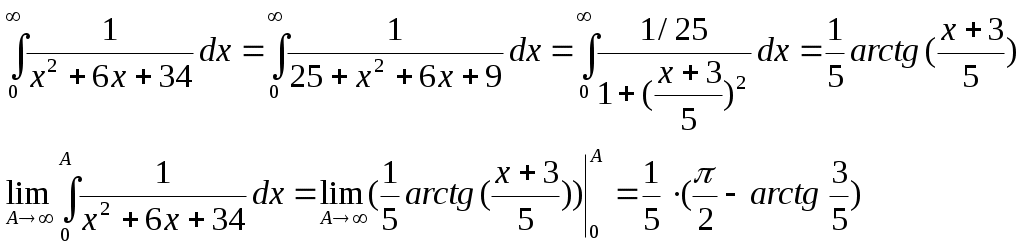 называется несобственным интегралом первого рода. Если существует и конечен, то несобственный интеграл первого рода называется сходящимся, если же он не существует или равен бесконечности, то несобственный интеграл первого рода называется расходящимся. Интеграл сходится.13.   Интеграл сходится.Выяснить сходимость несобственных интегралов 14.  Проверим на сходимость больший интеграл  .Несобственный интеграл вычисляем через предел:  Интеграл сходится, так как сходится больший интеграл.15.  .Подынтегральная функция имеет особенность в точке  . Находим порядок роста этой функции относительно 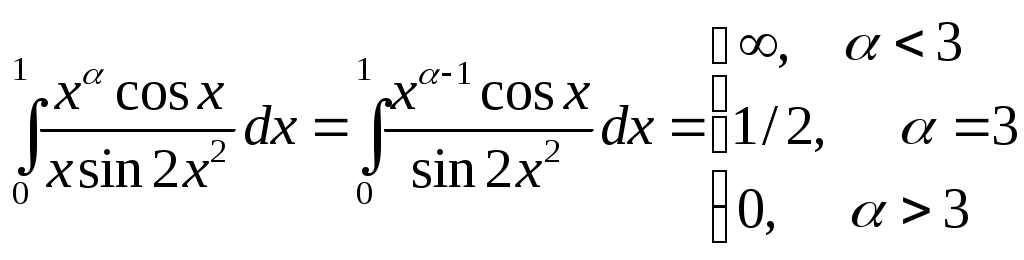 : Порядок роста равен 3, интеграл расходится.16. Найти площадь области, ограниченной линиями 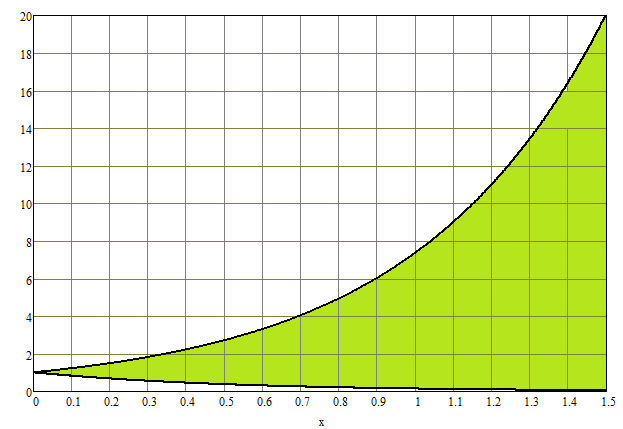   17. Найти длину дуги кривой 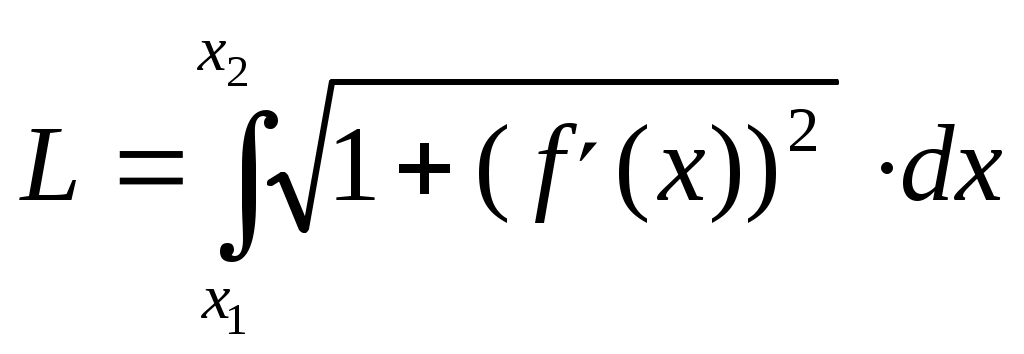  Производная:  Длина дуги кривой:  Список использованных источниковЕльцов А.А., Ельцова Т.А.Интегральное исчисление: методические указания по выполне- нию контрольных работ. — Томск: Факультет дистанционного обучения, ТУСУР, 2013. — 60 с. Ельцов А. А. Интегральное исчисление : учебное пособие / А. А. Ельцов, Т. А. Ельцова. — Томск : Эль Контент, 2013. — 138 с. |