Математика. Контрольная работа по дисциплине Математика Семестр 1 Вариант 2 студент гр. Иб360891 Богданов М. Ю
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение Высшего образования «Тульский государственный университет» Интернет-институт КОНТРОЛЬНАЯ РАБОТА По дисциплине «Математика» Семестр 1 Вариант 2 Выполнил: студент гр. ИБ360891 Богданов М. Ю. Проверил: д.ф.-м.н., проф. Христич Д. В. Тула, 2020 1. Для данного определителя 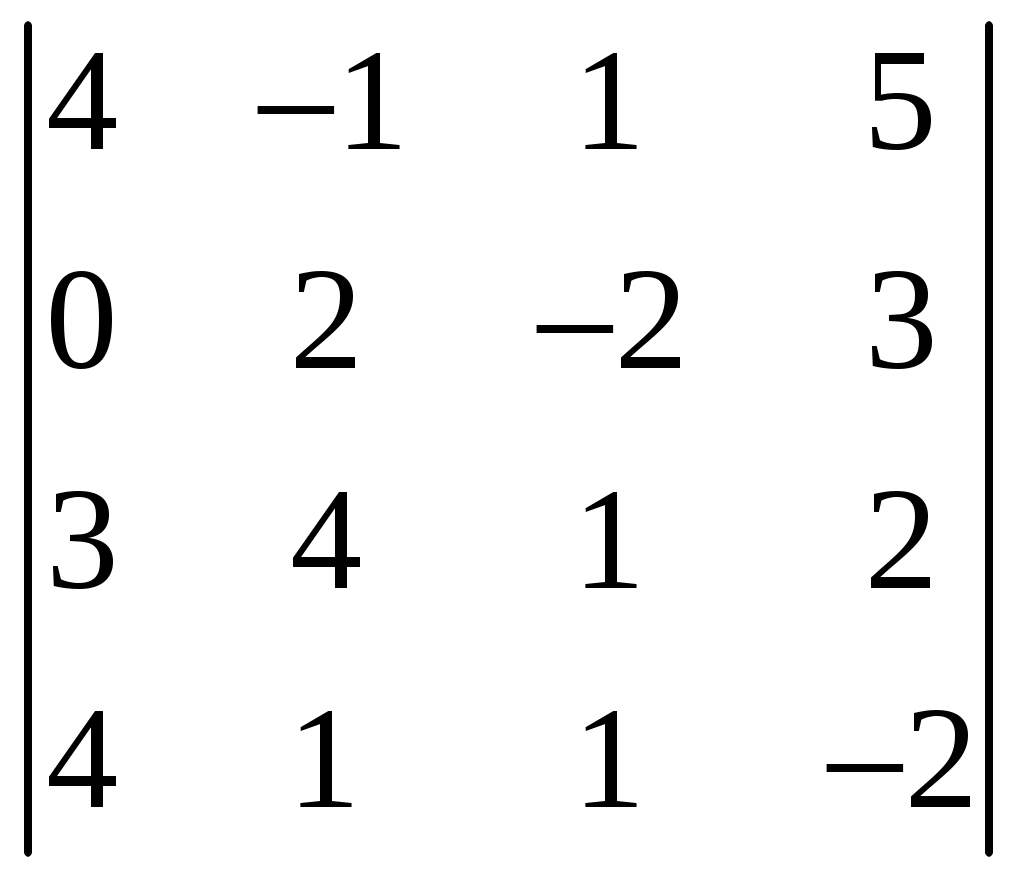 найти алгебраическое дополнение элемента найти алгебраическое дополнение элемента Решение. Минором Вычислим минор 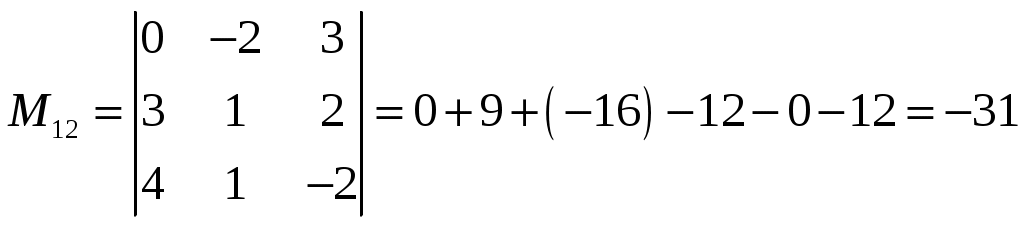 Алгебраическое дополнение Тогда Ответ: 31. 2. Найти матрицы 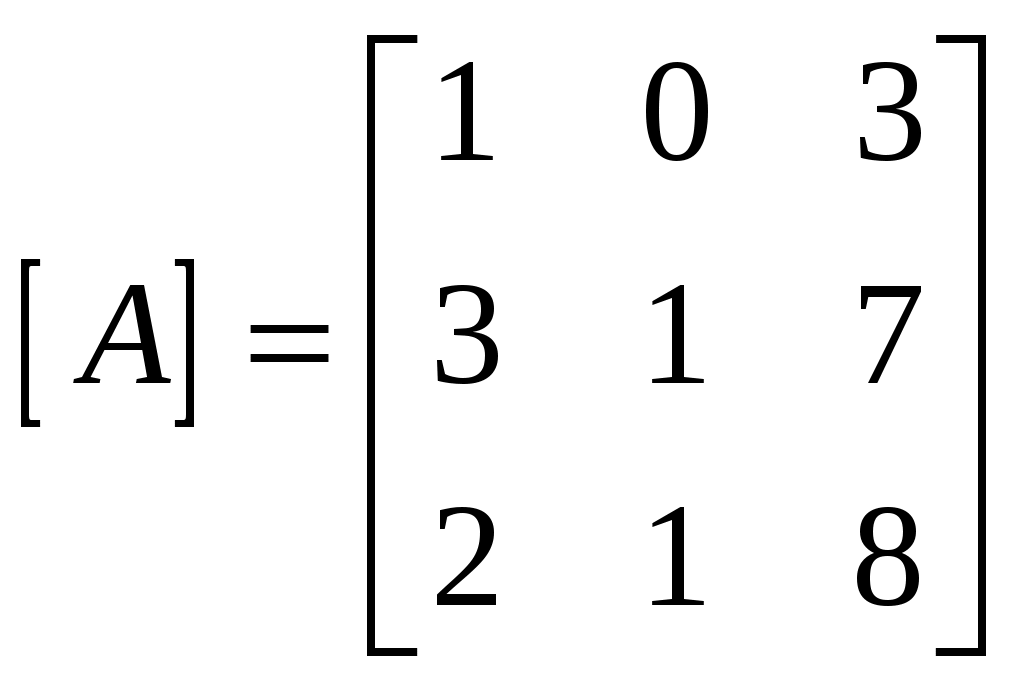 , , 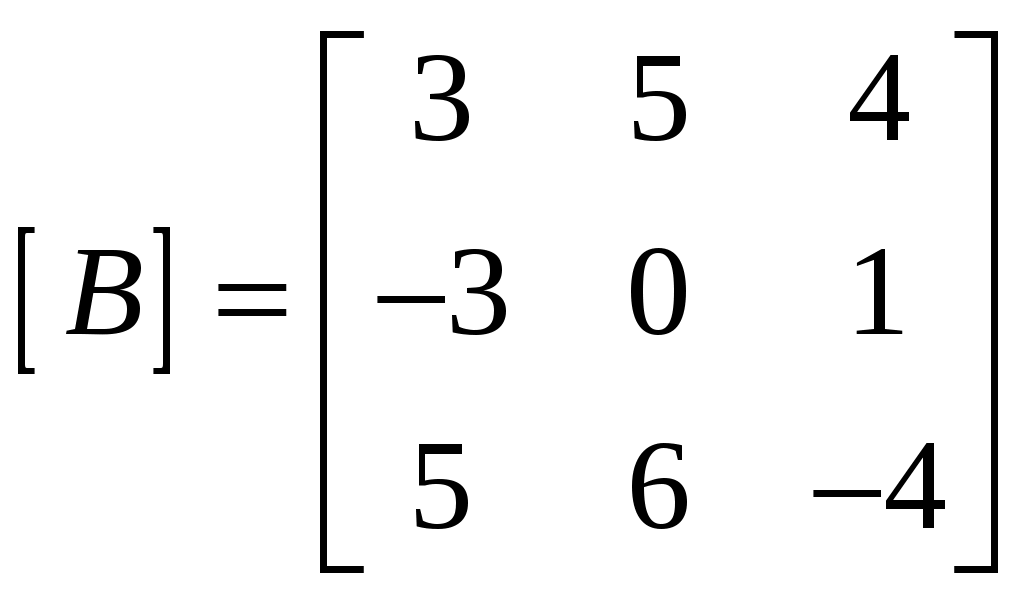 . .Решение. 1) Находим 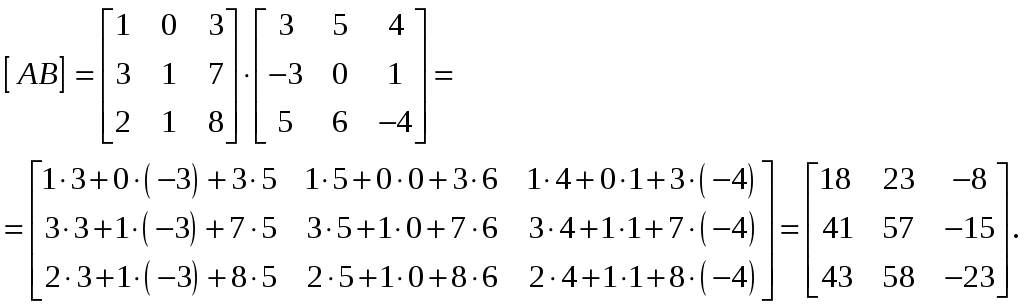 2) Находим 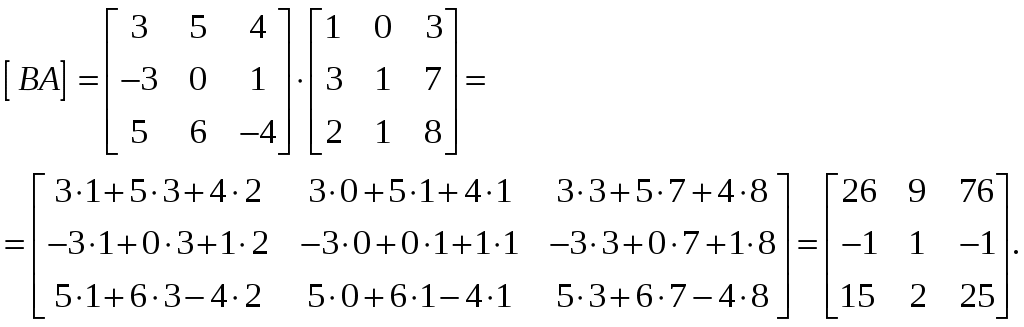 3) Найдем матрицу 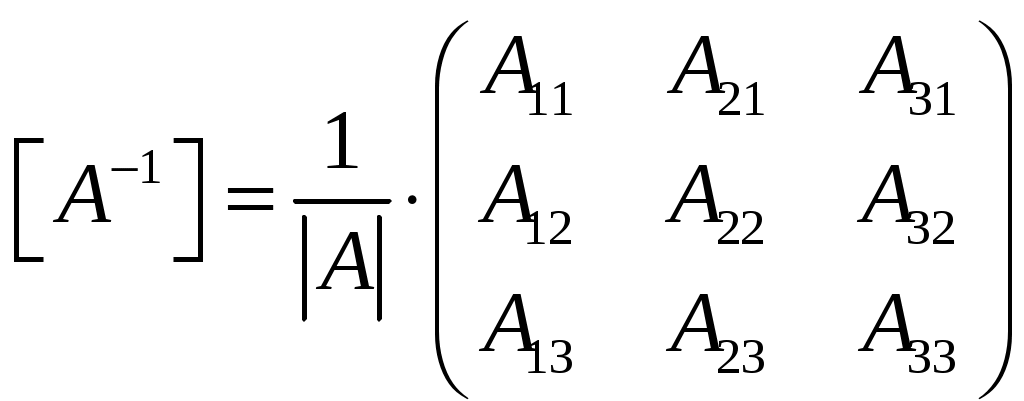 , где , где 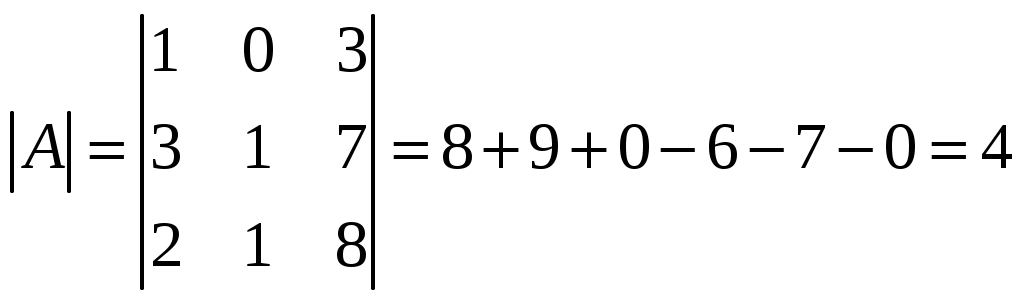 , ,
Обратная матрица имеет вид: 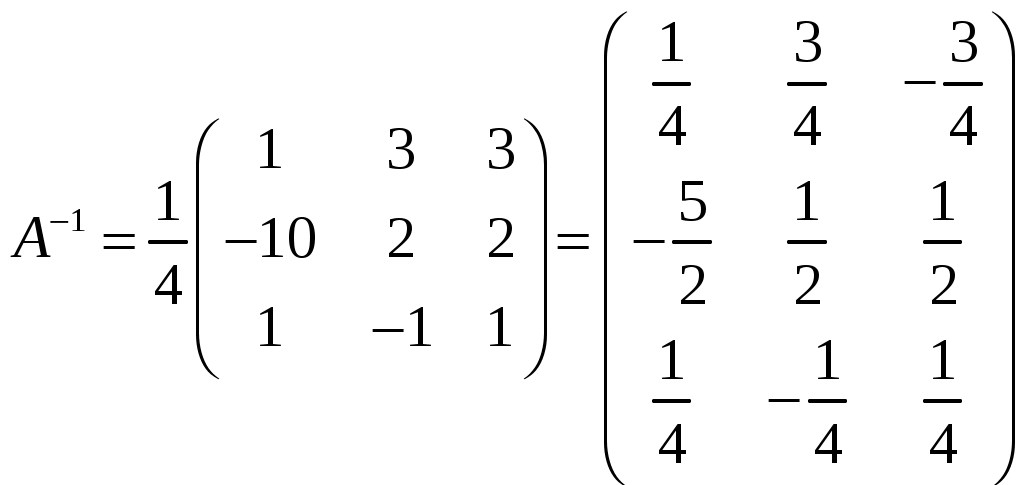 . .3. Проверить совместность системы уравнений и в случае совместности решить ее матричным методом . 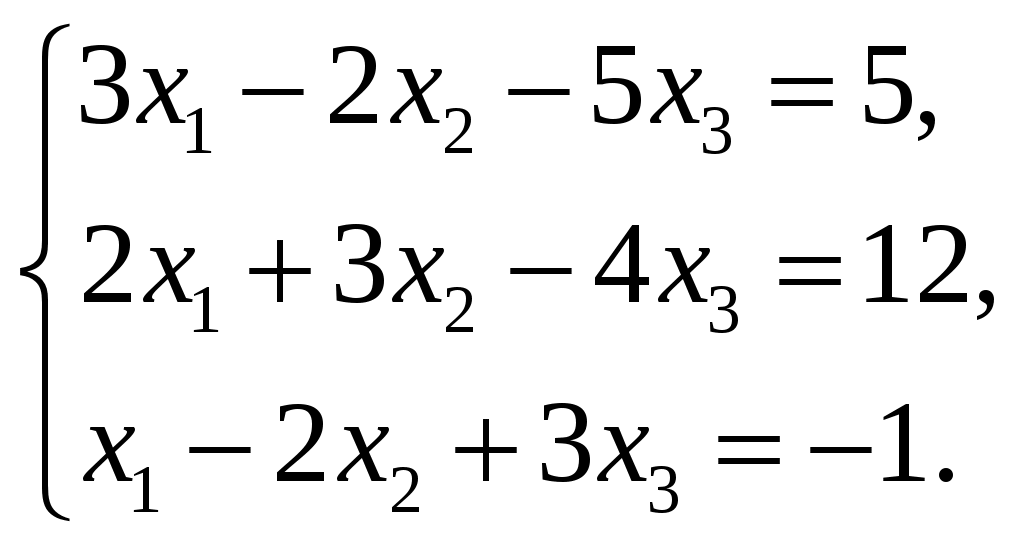 Решение. Совместность данной системы докажем, используя теорему Крамера, а именно: если главный определитель отличен от нуля, то система имеет единственное решение. Находим главный определитель системы: 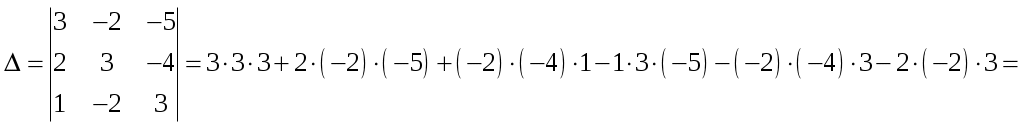 Решим заданную систему: Матричным способом. Для нахождения решения СЛАУ с помощью обратной матрицы запишем систему уравнений в матричной форме AX=B, где 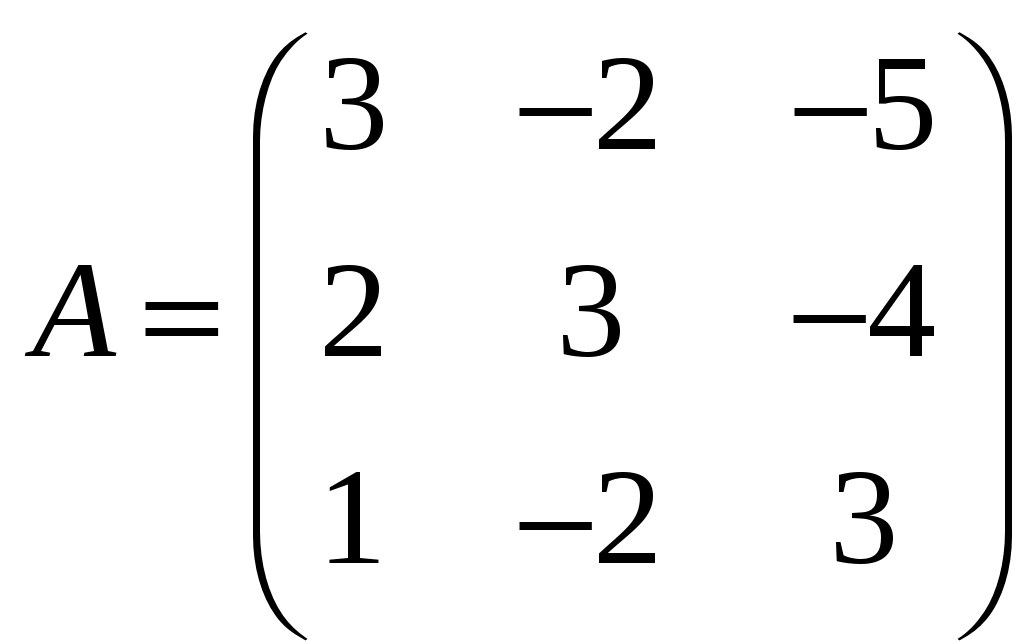 , , 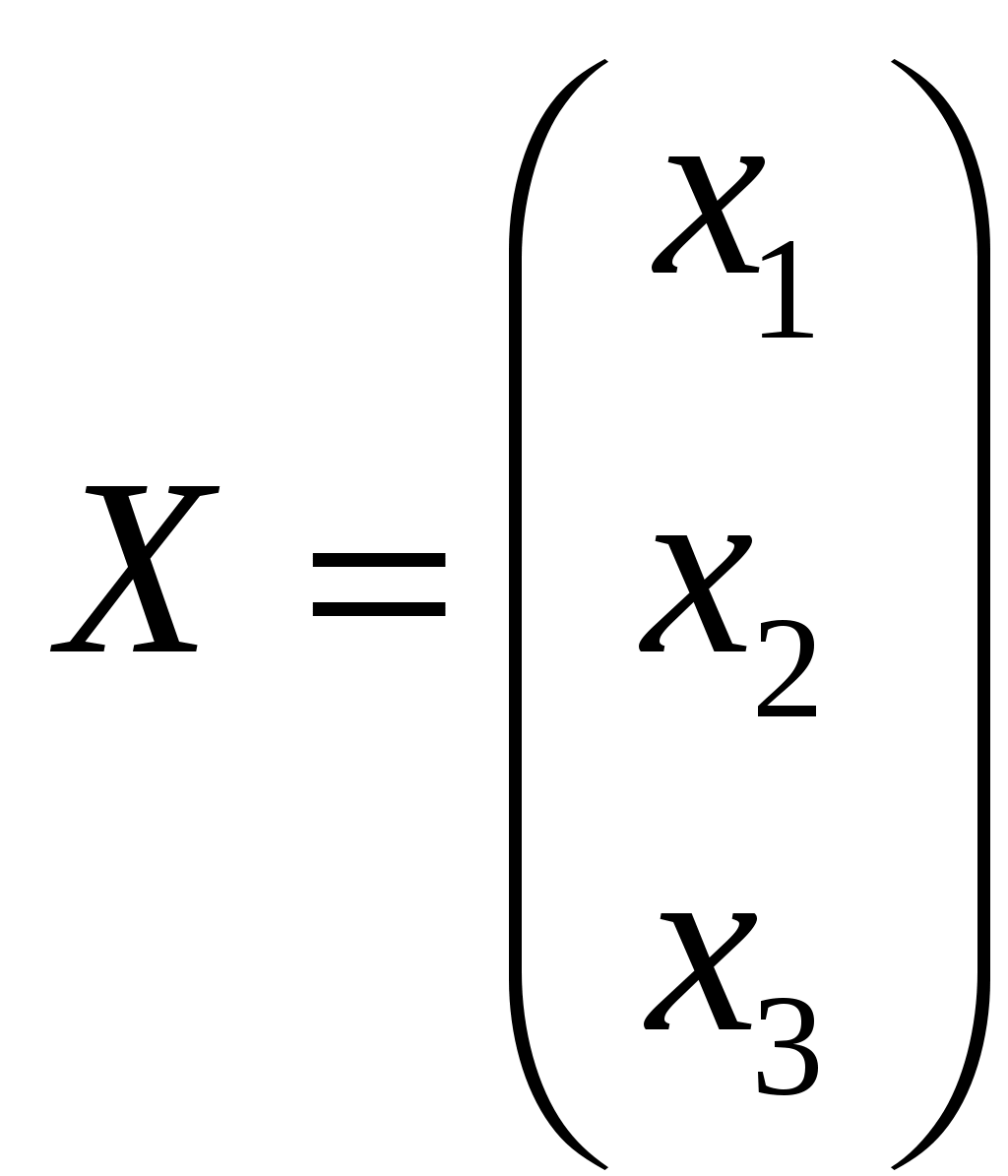 , , 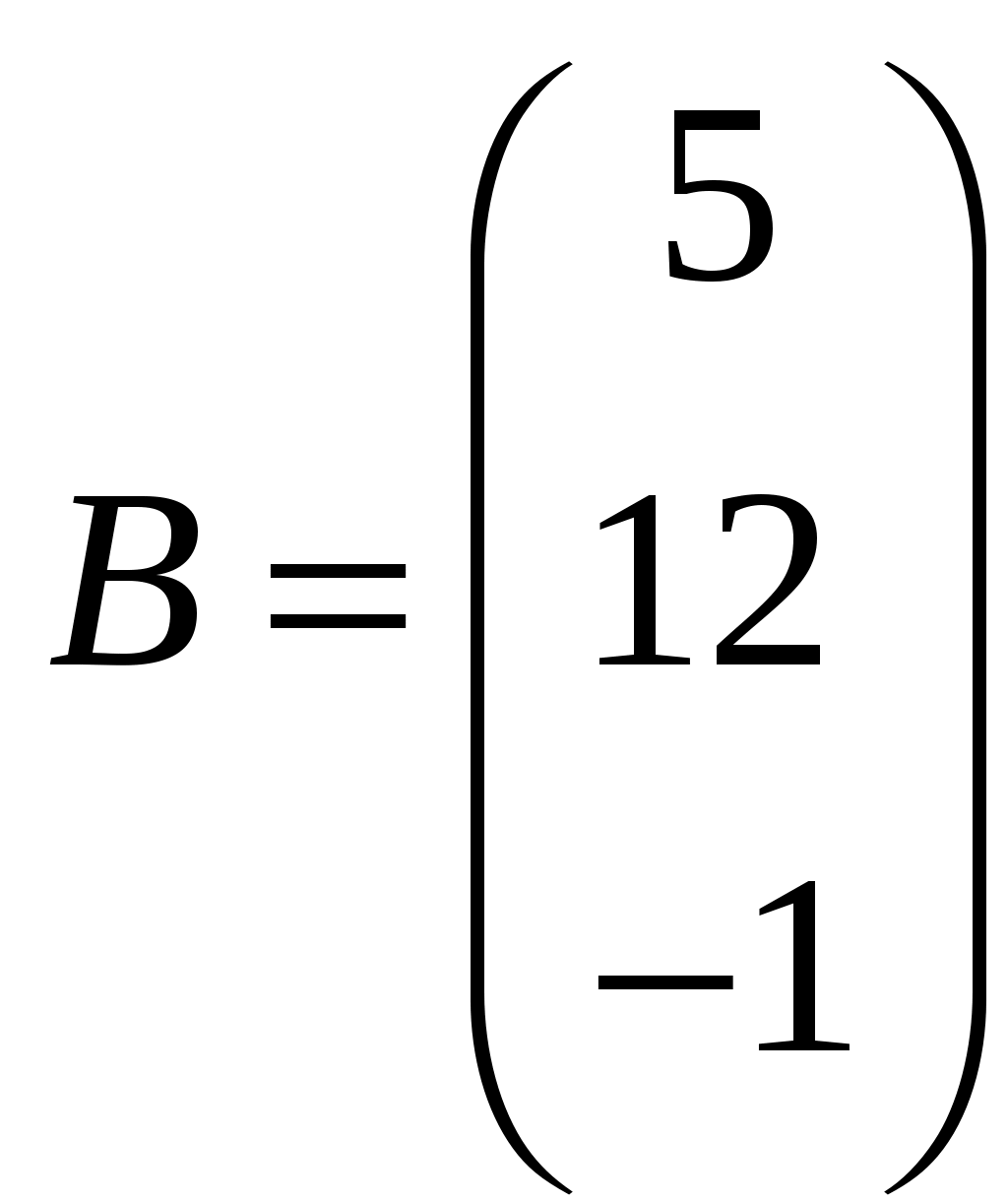 . .Решение СЛАУ в матричной форме имеет вид 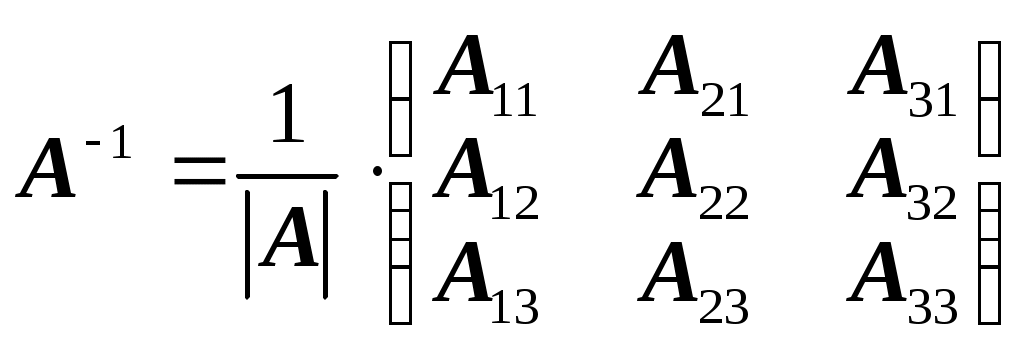 , где , где 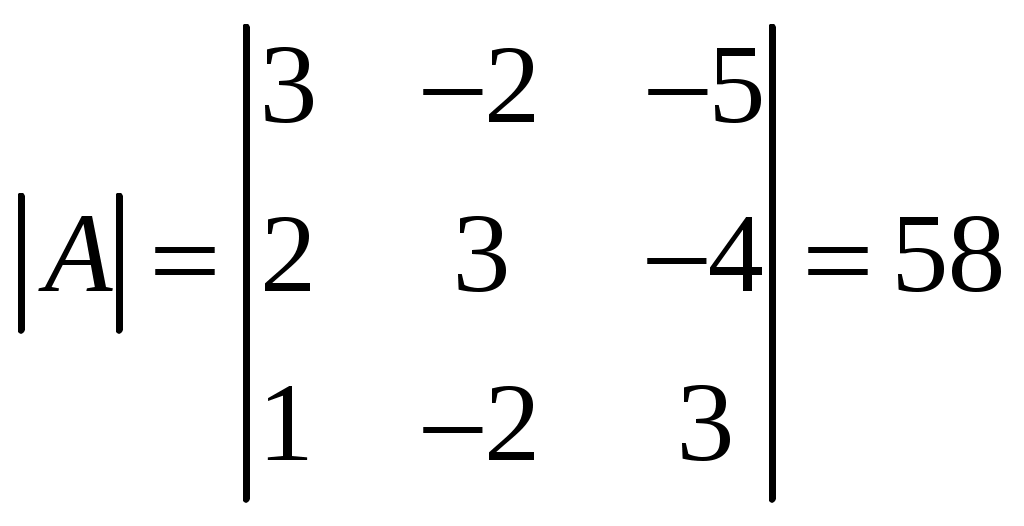 , ,
Обратная матрица имеет вид: 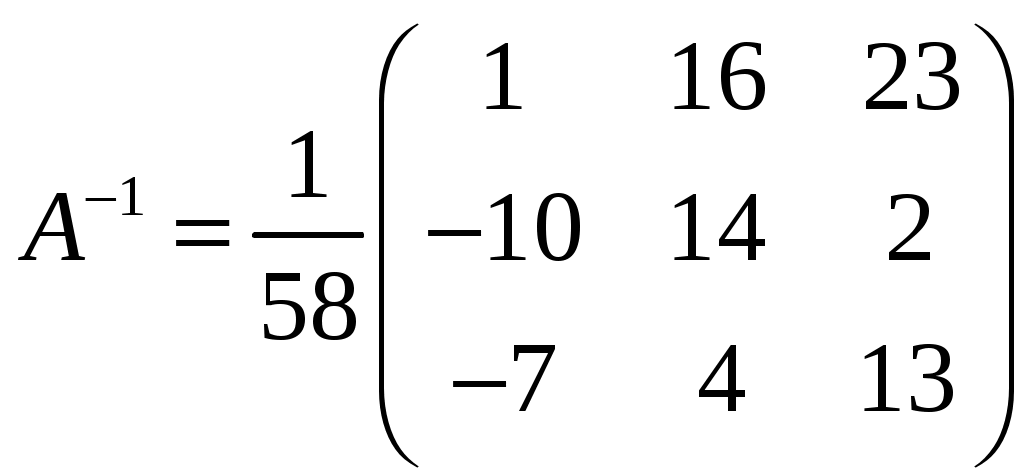 . .Итак: 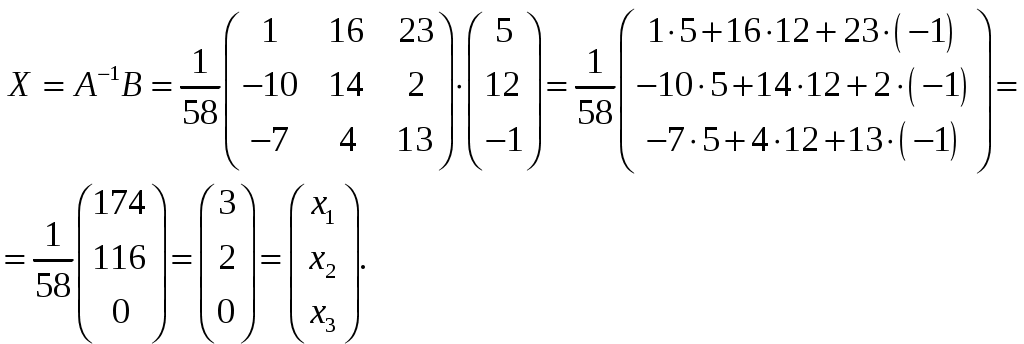 Итак, решение системы: Ответ: 4. Доказать, что векторы Решение. Векторы 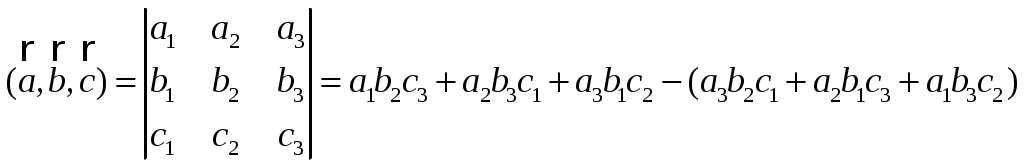 В данном случае, 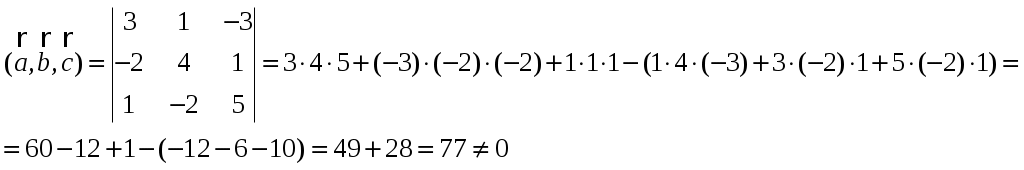 Так как Так как Для разложения вектора или в координатной форме 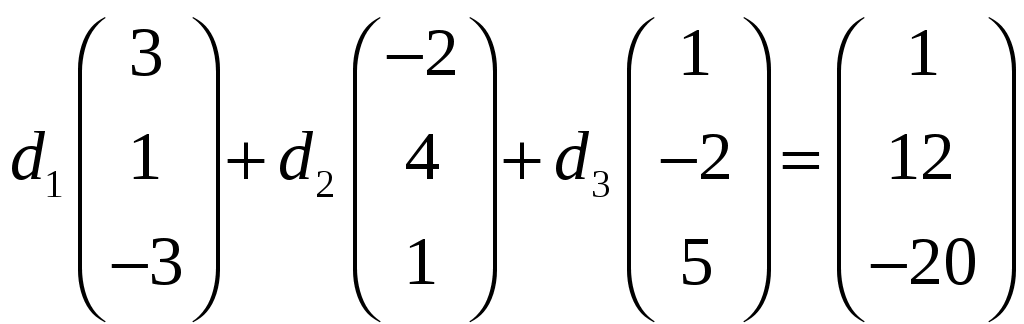 Задача сведена к решению системы 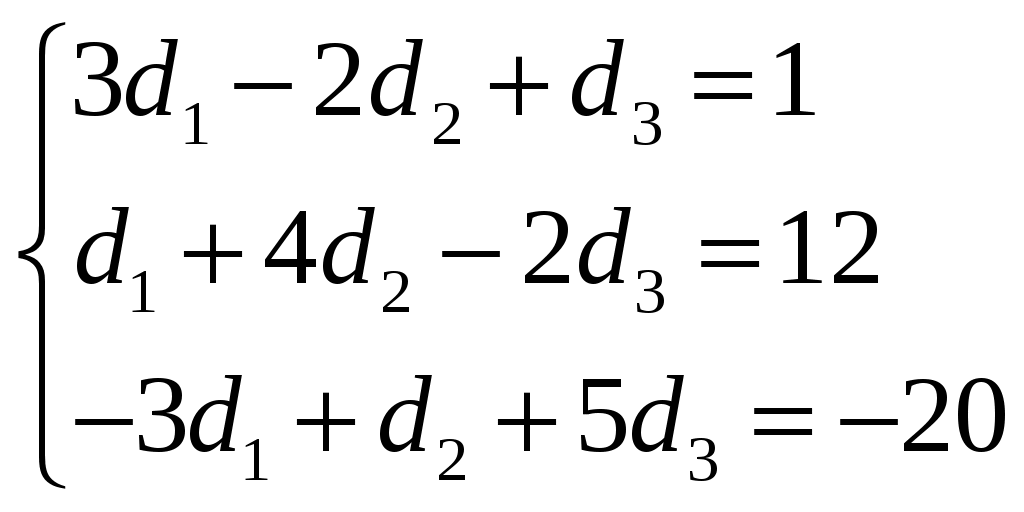 по формулам Крамера. Матрица коэффициентов и матрица-столбец свободных членов данной системы: 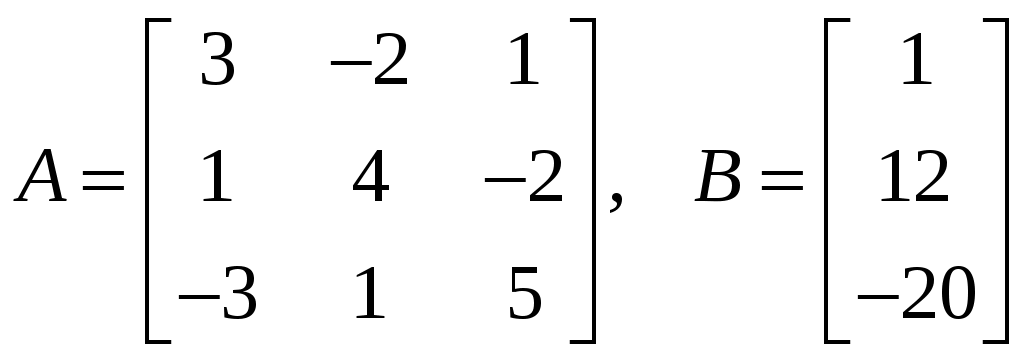 . .Определитель матрицы коэффициентов 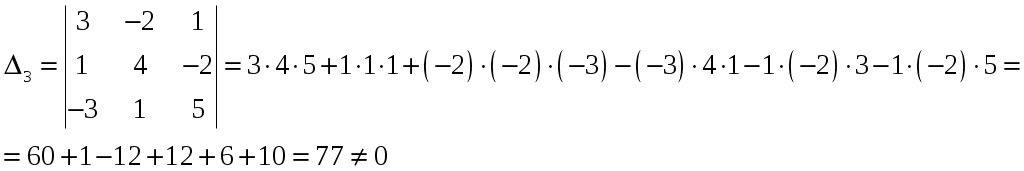 поэтому систему уравнений можно решить по формулам Крамера: Так как 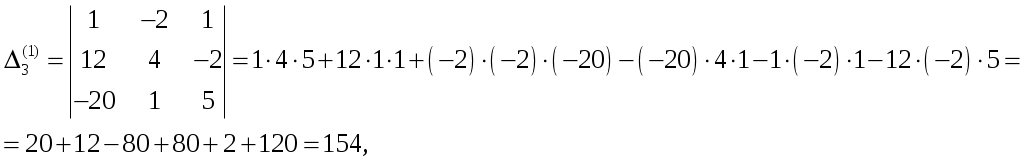 то 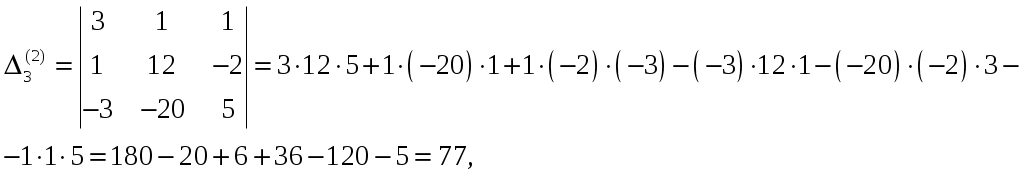 , , то 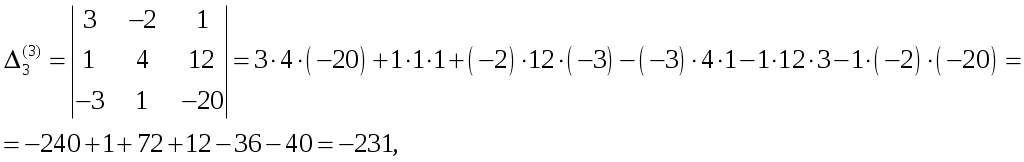 , , то Таким образом, в базисе 5. Вершины пирамиды находятся в точках А(7,4,9), В(1,−2,−3), С(−5,−3,0), D(1,−3,4). Найти объем пирамиды и длину высоты, опущенной из вершины С. Решение. Объем пирамиды находится по формуле: 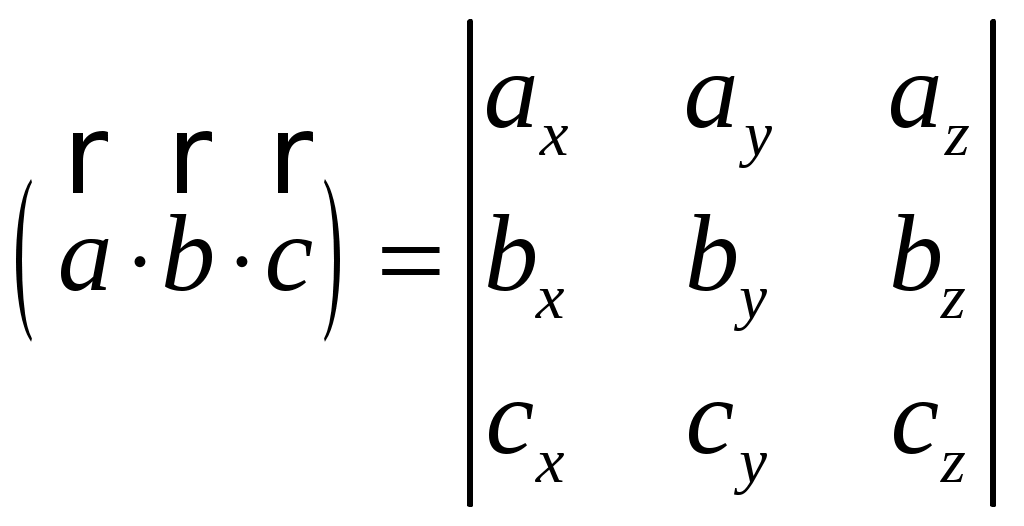 . .Найдем координаты векторов, используя формулу: 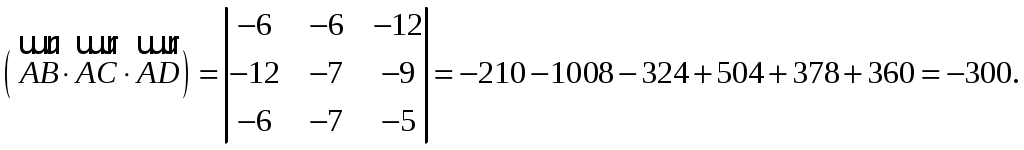 Для нахождения длины высоты, опущенной из вершины C на грань ABD найдем сначала площадь грани ABD. 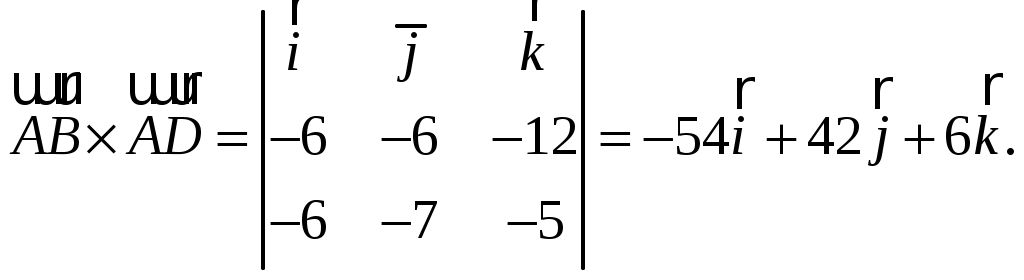 Sосн = Т.к. V = 6. Найти расстояние от точки Решение. Расстояние от точки Найдем уравнение плоскости проходящей через точки Воспользуемся уравнением плоскости, проходящей через три точки 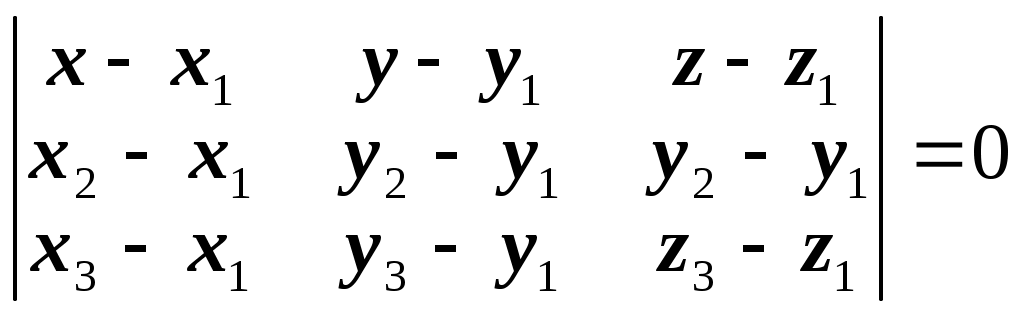 Для нашей задачи имеем: 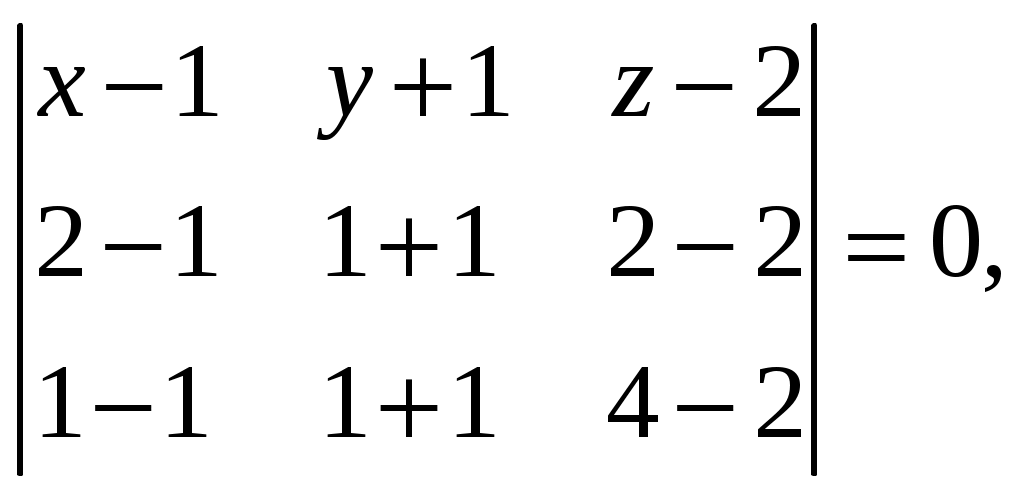 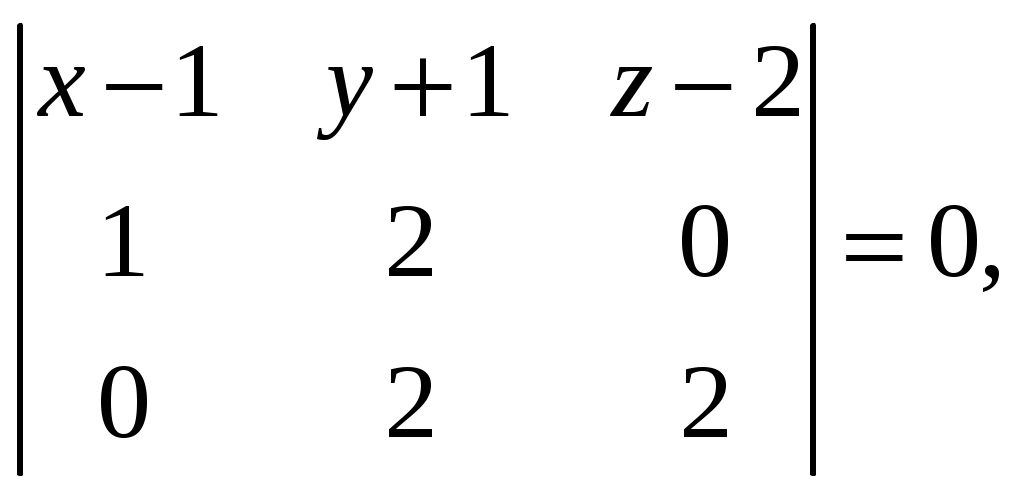 Тогда расстояние от точки 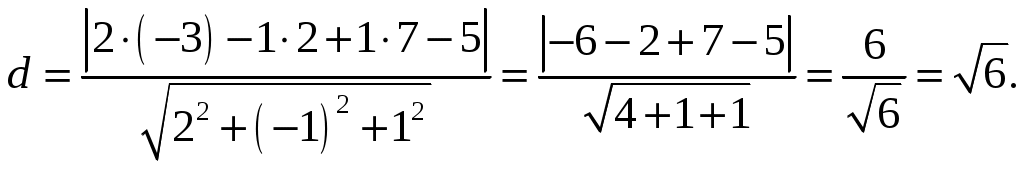 7. Написать канонические уравнения прямой Решение. Канонические уравнения прямой, проходящей через точку Перейдем к канонической форме уравнения прямой. Находим точку на данной прямой. Пусть Направляющий вектор прямой найдем из векторного произведения нормальных векторов пересекаемых плоскостей, т.е. 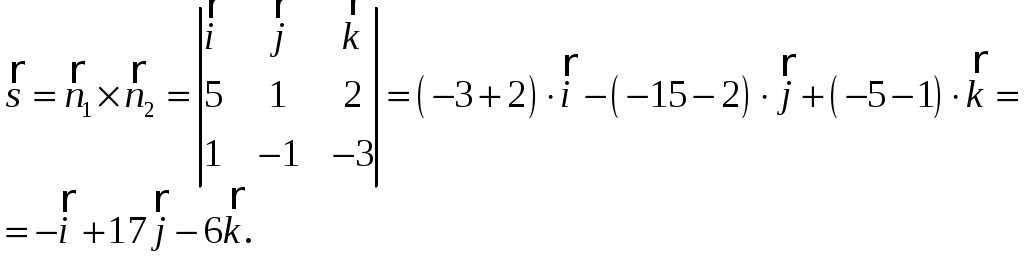 Т.е. Получаем канонические уравнения прямой: Ответ: 8. Найти точку пересечения прямой, заданной каноническими уравнениями, и плоскости. Решение. Запишем уравнение прямой, заданной каноническими уравнениями, в параметрической форме: 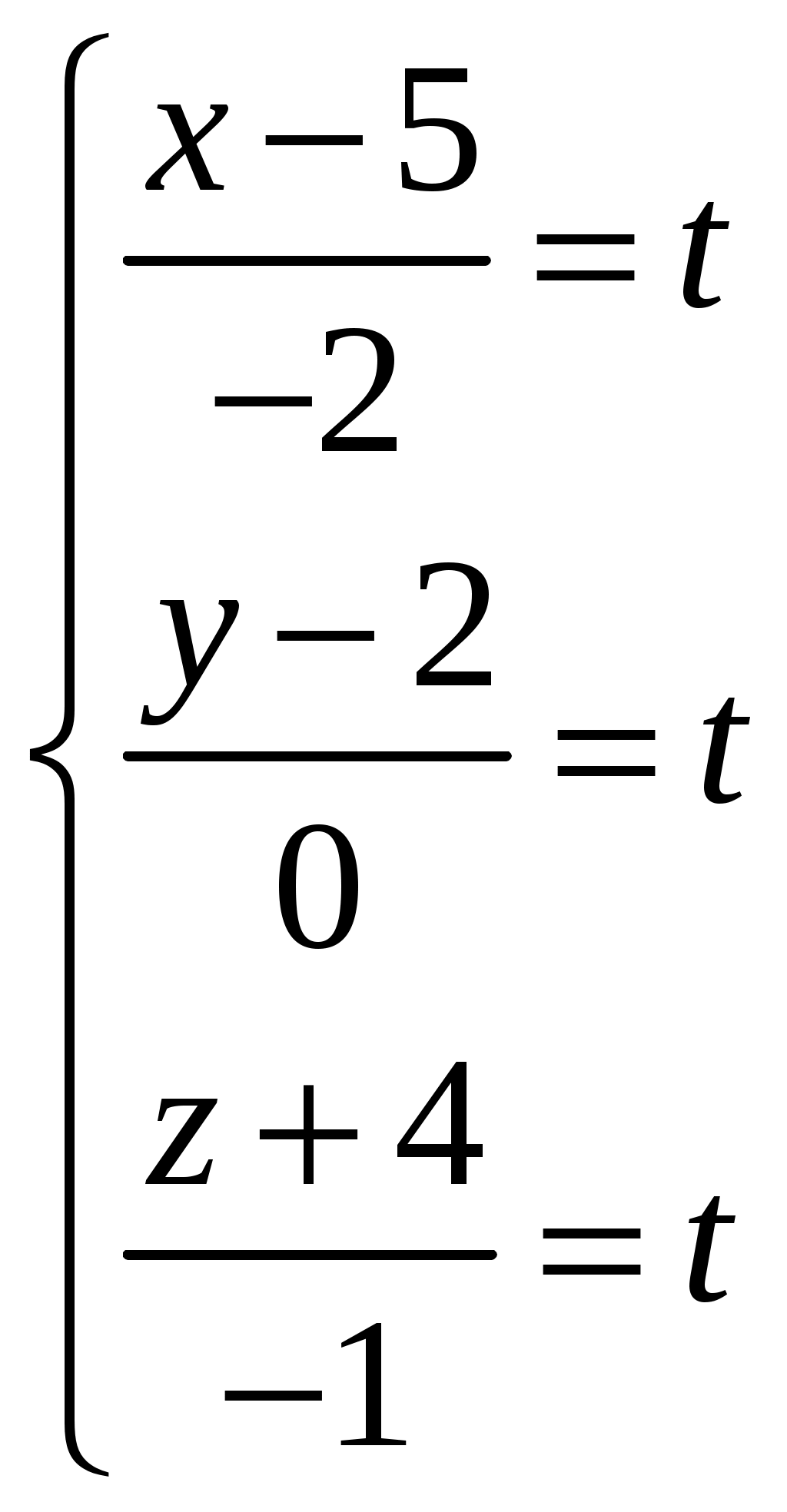 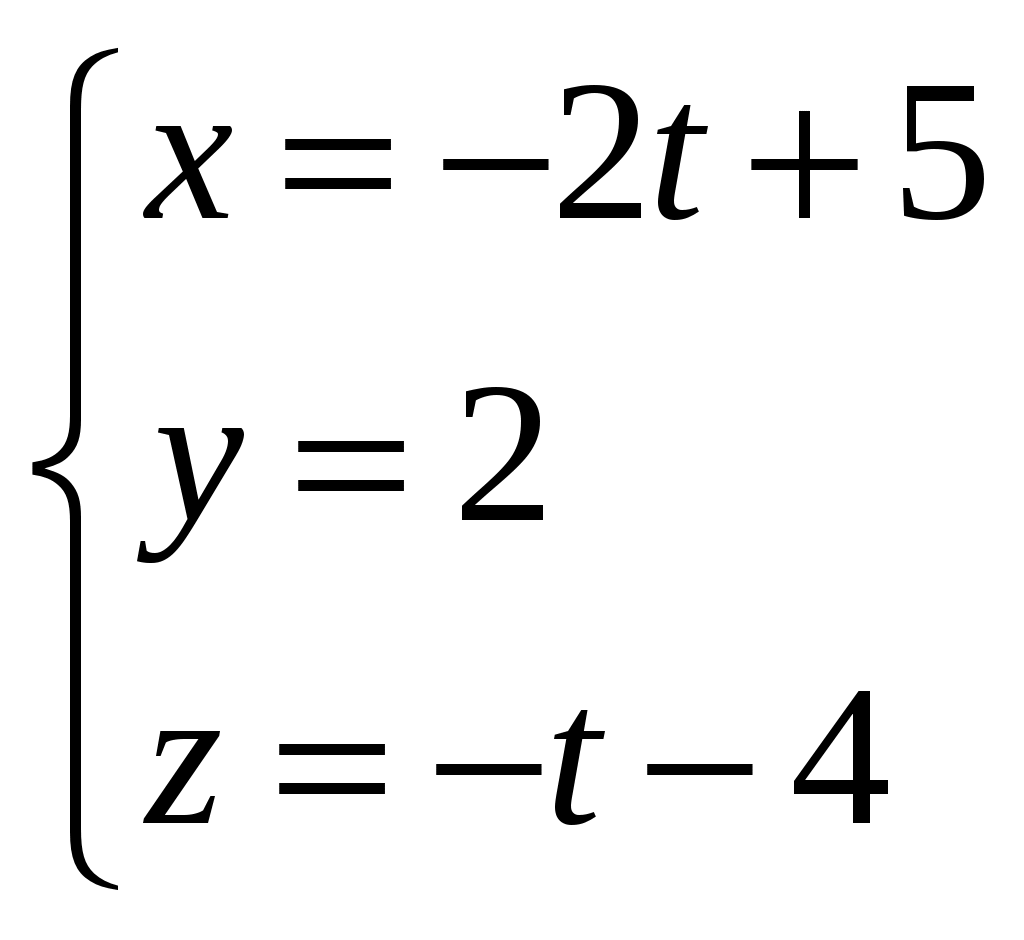 Подставляя эти выражения для x, y, z в уравнение плоскости, находим значение параметра t , при котором происходит пересечение прямой и плоскости: Подставляя в параметрические уравнения прямой найденное значение 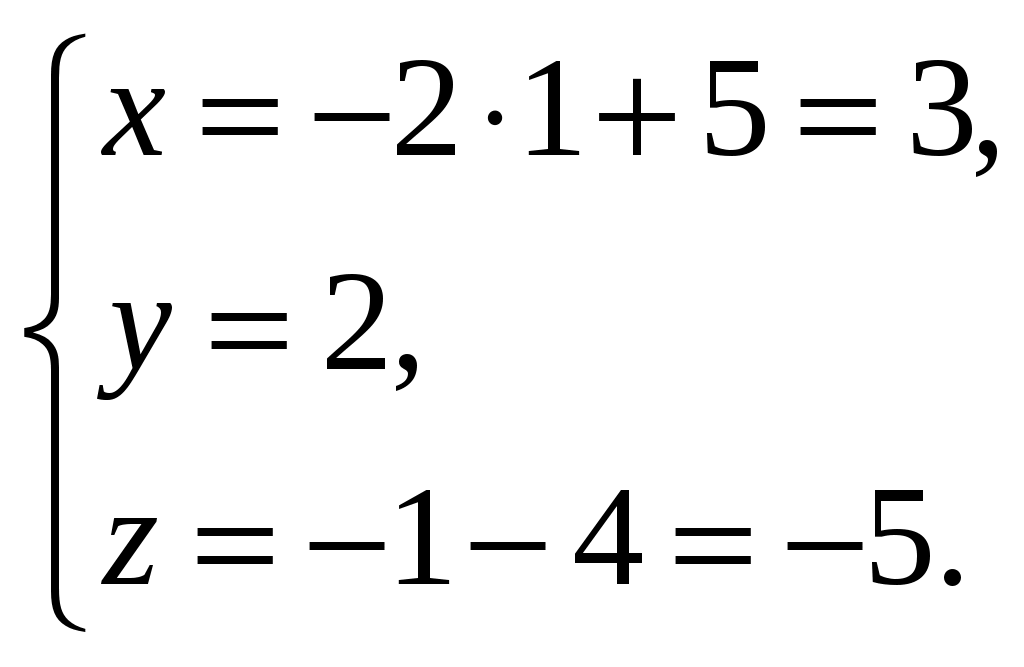 Таким образом, точка пересечения прямой и плоскости есть Ответ: 9. Вычислить предел Решение. Непосредственная подстановка предельного значения аргумента x=0 приводит к неопределенности Т.к. 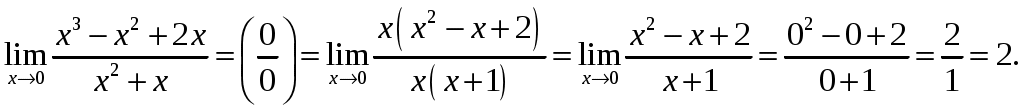 . .Ответ: 2. 10. Вычислить предел Решение. В этом случае имеем неопределенность вида 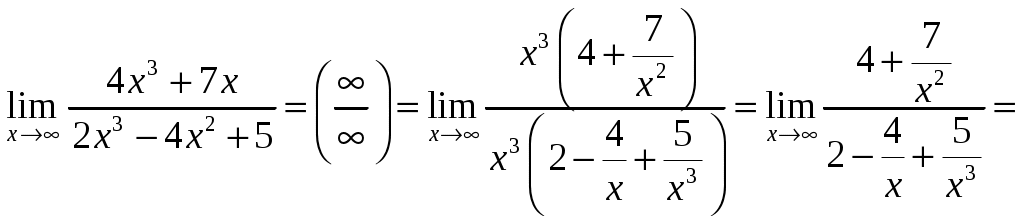 Ответ: 2. 11. Вычислить предел Решение. Под знаком предела есть иррациональность в числителе дроби. Непосредственная подстановка предельного значения аргумента x= –4 приводит к неопределенности вида Чтобы раскрыть эту неопределенность, достаточно числитель и знаменатель дроби, стоящей под знаком предела, домножить на выражение, сопряженное числителю дроби: 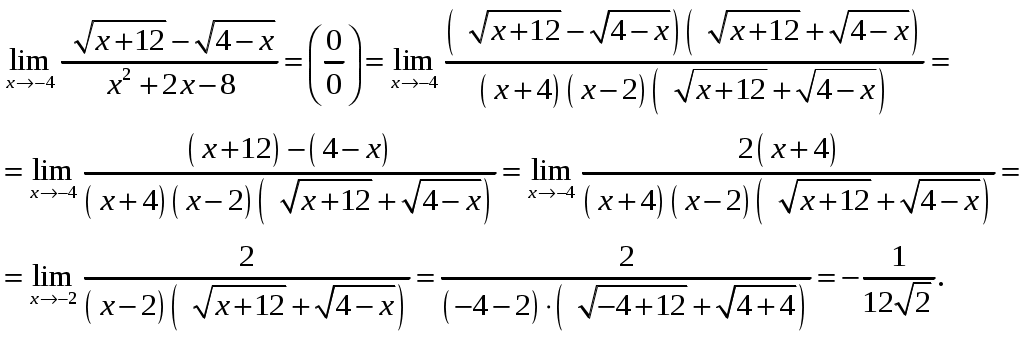 Ответ: 12. Вычислить предел Решение. При x=0 числитель и знаменатель дроби равны 0, имеем неопределённость вида 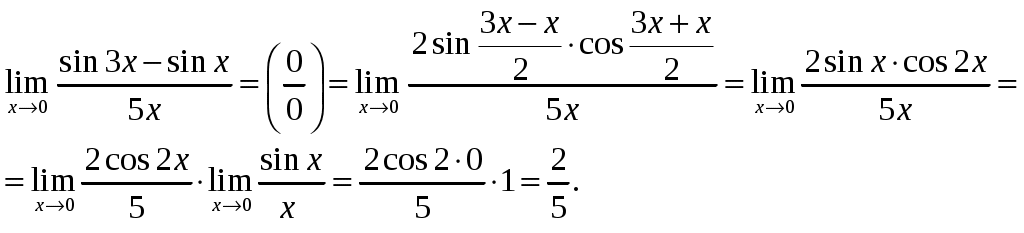 Ответ: 13. Вычислить предел Решение. 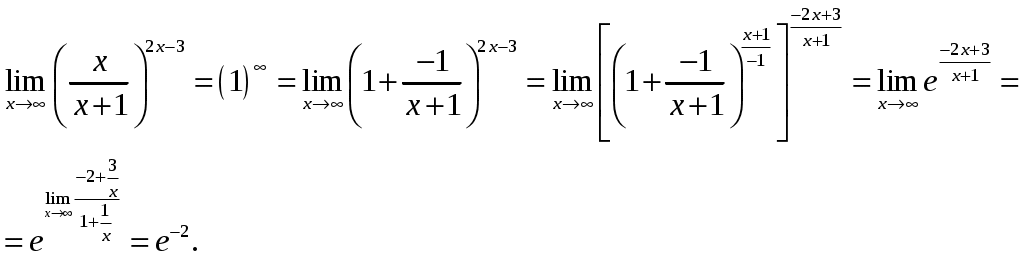 При вычислении этого предела использована обобщенная формула второго замечательного предела 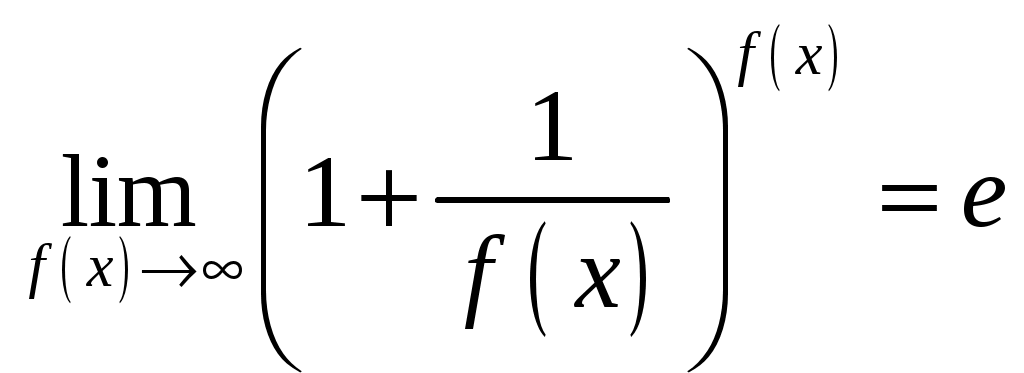 и теорема о пределе показательно-степенной функции: и теорема о пределе показательно-степенной функции: Ответ: 14. Составить уравнение касательной к данной кривой в точке с абсциссой Решение. Уравнение касательной: Находим Находим производную функции и вычисляем ее значение при Тогда уравнение касательной: Ответ: 15. Найти дифференциал функции в точке с абсциссой Решение. Дифференциал функции Находим производную функции Применим правила дифференцирования сложной функции: 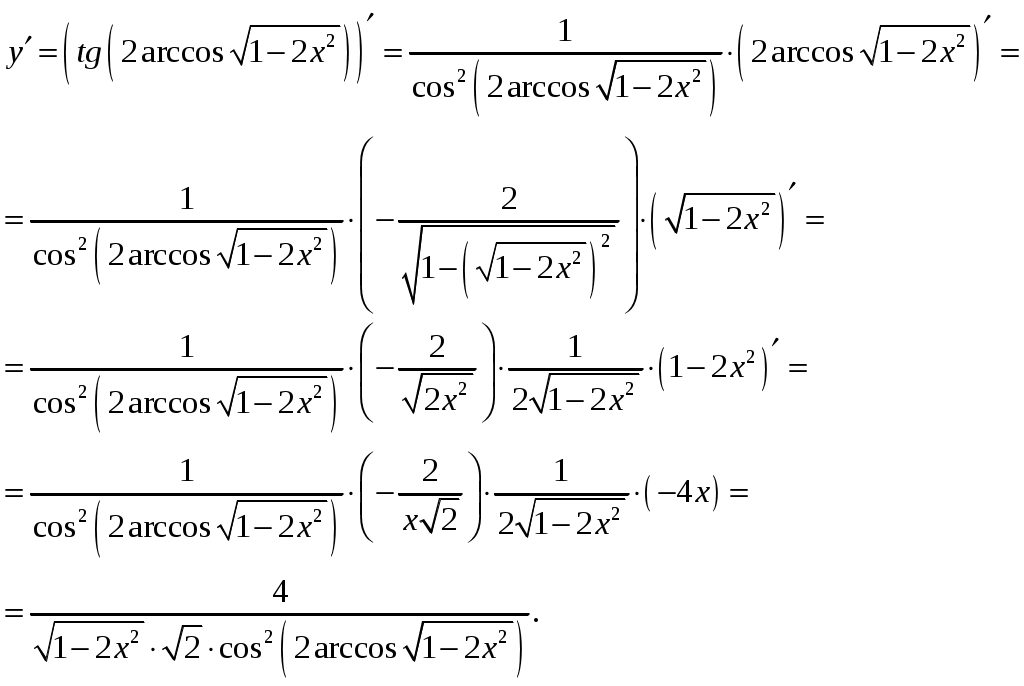 В заданной точке: 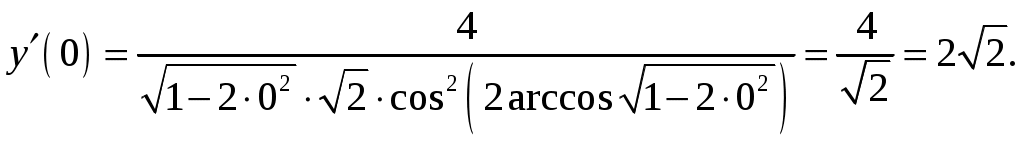 Тогда дифференциал: Ответ: |
