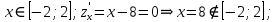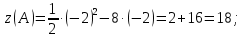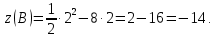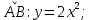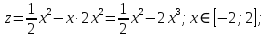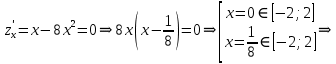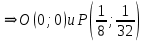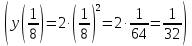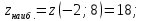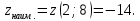математика. Контрольная работа по дисциплине Математика Семестр 2 Вариант 2 Проверил Тула 2021
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» Интернет-институт КОНТРОЛЬНАЯ РАБОТА по дисциплине «Математика» Семестр 2 Вариант 2 Выполнил: Проверил: Тула 2021 Провести полное исследование функции и построить её график: 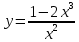 Область определения : 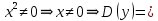 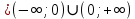 Функция не является ни чётной, ни не чётной, т.к. 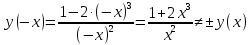 Функция непериодическая. Асимптоты. а) Исследуем точку разрыва 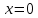 на наличие вертикальной асимптоты на наличие вертикальной асимптоты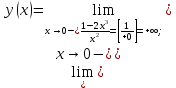 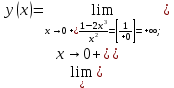 Т.к. односторонние пределы бесконечны, в точке 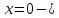 разрыв II рода; разрыв II рода;Прямая 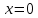  вертикальная асимптота. вертикальная асимптота.б) Найдём наклонную асимптоту 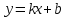 по формуле по формуле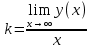 , , 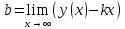 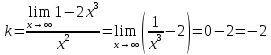 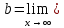 ( (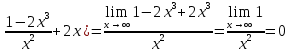 Значит, прямая 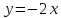 наклонная асимптота. наклонная асимптота.Интервалы монотонности и экстремумы функции 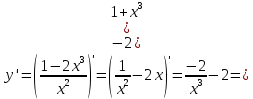 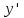 существует на существует на 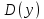 , решаем уравнение , решаем уравнение 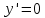 : :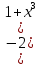 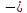 критическая точка критическая точкаПолучили: функция возрастает на интервале ( 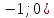 , убывает на интервале ( , убывает на интервале (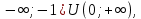 имеем минимум: имеем минимум: 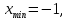 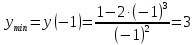 ( 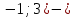 точка минимума. точка минимума.Интервалы выпуклости, вогнутости, точка перегиба. 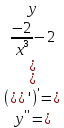 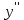 существует на существует на 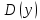 ; уравнение ; уравнение 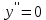 корней не имеет ⇒ корней не имеет ⇒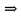 нет критических точек II рода; нет критических точек II рода;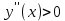 на на 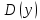 . Следовательно, график функции . Следовательно, график функции  вогнутый на всей области определения, точек перегиба нет. вогнутый на всей области определения, точек перегиба нет.Точки пересечения с осями координат. С осью 0y  точек пересечений нет, т.к. прямая точек пересечений нет, т.к. прямая 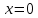 (ось 0y) (ось 0y)  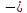 вертикальная асимптоты вертикальная асимптотыС осью 0x: 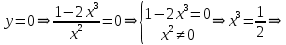 ⇒ 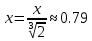 ; ;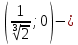 точка пересечения с осью 0x точка пересечения с осью 0xДополнительные точки: 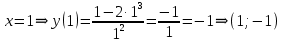 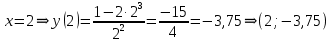 График функции. 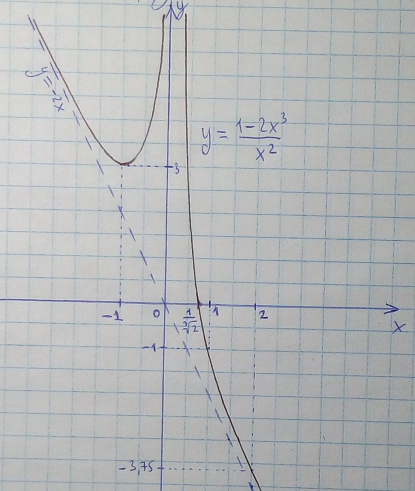 Найдите действительную часть комплексного числа 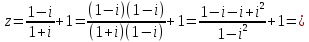 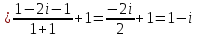 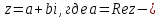 действительная часть. В данном случае: действительная часть. В данном случае: 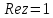 . .Ответ: 1. Найти неопределенный интеграл 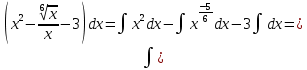 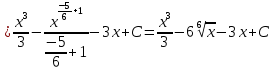 Найти неопределенный интеграл. 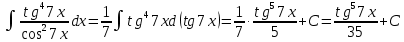 Найти неопределенный интеграл. 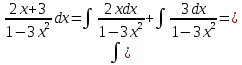 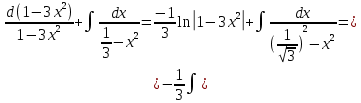 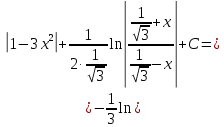 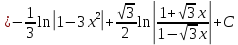 Найти неопределенный интеграл. 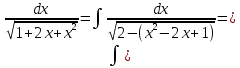 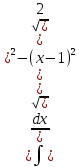 Найти неопределенный интеграл. 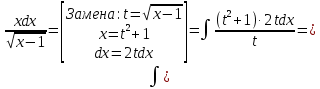 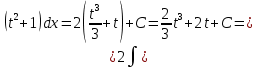 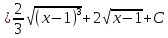 Вычислить определенный интеграл. 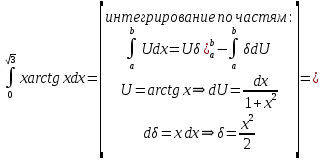 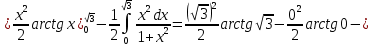 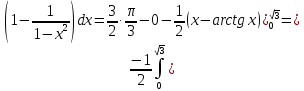 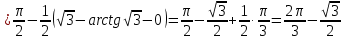 Ответ: 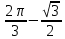 Вычислить определенный интеграл. 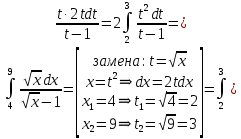 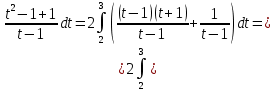 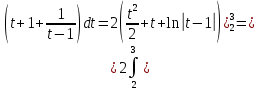 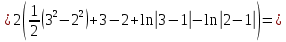 |

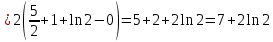
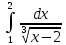
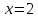
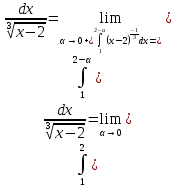
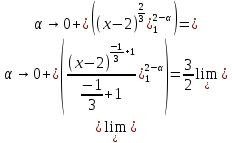
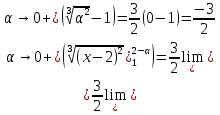
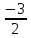 .
.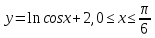
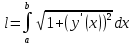
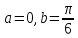
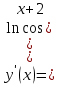
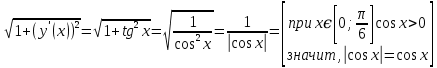 =
=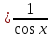
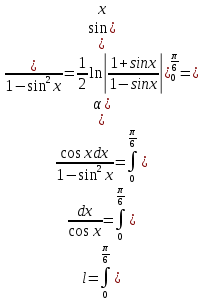
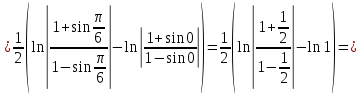
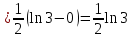
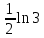 .
.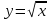 ,
, 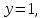
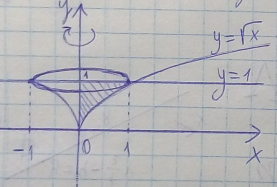
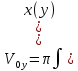
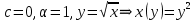
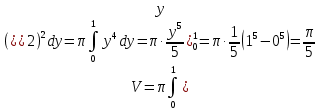
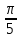 куб.ед.
куб.ед.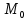 .
.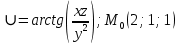
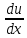 ,
,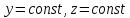
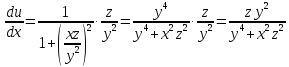
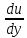 ,
,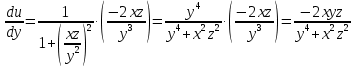
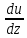 ,
,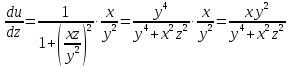
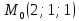 :
: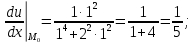
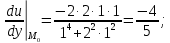
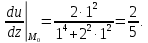
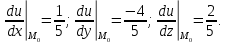
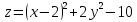
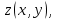 используя необходимые условия экстремума:
используя необходимые условия экстремума: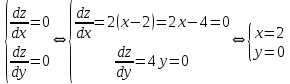
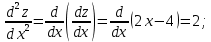
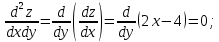
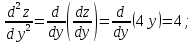
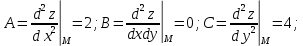
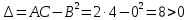
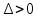 и
и 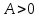 , функция
, функция 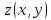 имеет в точке М минимум:
имеет в точке М минимум: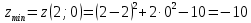
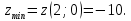
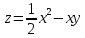 в области D:
в области D: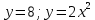
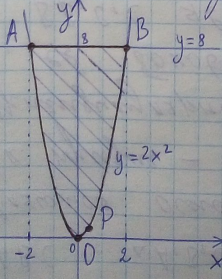
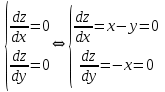
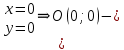 критическая точка, принадлежащая D
критическая точка, принадлежащая D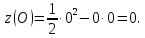
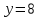 ;
; 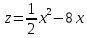 ;
;