мжг 4 вариант. МЖГ 4 вариант. Контрольная работа по дисциплине Механика жидкости и газа Вариант 1 Исполнитель
 Скачать 245.08 Kb. Скачать 245.08 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Казанский национальный исследовательский технический университетим. А.Н. Туполева-КАИ» (КНИТУ-КАИ) Лениногорский филиал (наименование института (факультета), филиала) Кафедра Машиностроения и информационных технологий (наименование кафедры) 15.03.01 Машиностроение (шифр и наименование направления подготовки (специальности)) Контрольная работа по дисциплине: «Механика жидкости и газа»______________ Вариант 1
Лениногорск 2021 Задача 1.1.1 На свободную поверхность закрытого резервуара, наполненного нефтью ( ρ=850 кг/м3), действует давление Ризб. На глубине h от свободной поверхности жидкости к резервуару присоединены: пружинный манометр М, пьезометр и U-образный ртутный манометр (δрт=13,6). Определить показания приборов.  Исходные данные Ризб = 2,4 атм = 2,4 бар h = 2,0 м; а = 0,1 м Решение Составим уравнение равновесия относительно нижней границы резервуара   = 13600 кг/м³ - плотность ртути = 13600 кг/м³ - плотность ртути = 850 кг/м³ - плотность нефти = 850 кг/м³ - плотность нефтиТогда показание ртутного U –образного манометра составит  м м Показание пьезометра составит   м мПоказание пружинного манометра М,  Па=252,1 кПа Па=252,1 кПаЗадача 1.1.2 Какую силу Р2 необходимо приложить к большому поршню, чтобы система находилась в равновесии? Трубки заполнены водой (γв = 9,81·103 Н/м3), весом поршней пренебречь. 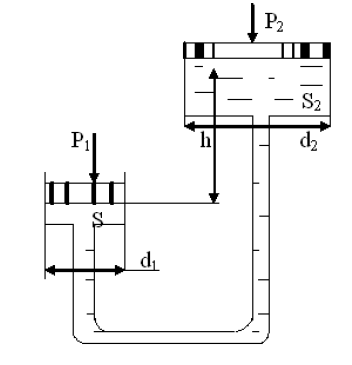 Исходные данные: Р1 = 250 Н; d1 =20 мм = 20·10-3 м; d2 =150 мм = 0,15 м; h = 450 мм = 0,45 м. Решение Составим уравнение равновесия относительно плоскости сравнения: 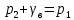 Давление под левым поршнем:  где  – площадь сечения малого поршня. – площадь сечения малого поршня.Тогда  ; ;Тогда давление под правым поршнем:  Тогда необходимое усилие на большом поршне: 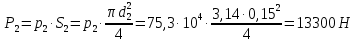 Задача 2.1.1 По напорному трубопроводу перекачивается загрязненная жидкость. Известно, что осаждение загрязнений в трубопроводе будет исключено, если жидкость будет двигаться со скоростью V ≥ 1,5 м/с. Найти максимально допустимый диаметр трубопровода, при котором не будет наблюдаться отложение взвеси, если вода, вытекая из трубопровода, заполняет резервуар объемом W за время t. Исходные данные: W = 1,5 м3; t = 5 мин = 300 с. Решение Расход жидкости определяется по формуле:  Так же расход жидкости можно найти по формуле: где Подставляя выражение (2) в выражение (1), получаем: откуда находим максимально допустимый диаметр трубопровода   Задача 2.2.1 Для измерения расхода воды, протекающей по трубопроводу диаметром d, установлено сопло диаметром d1. Разность уровней в пьезометрах h. Определить расход воды Q. Изменится ли перепад h, если вместо воды в трубе будет протекать нефть при том же расходе? Потерей напора между сечениями, в которых присоединены пьезометрические трубки, пренебречь.  Исходные данные d = 80 мм d1 = 35 мм h = 1,3 м Решение Составим уравнение неразрывности и уравнение Бернулли для сечений 1-1 и 2-2. 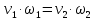 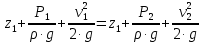 Или   так как  . .Преобразуя эти уравнения, получим  Откуда 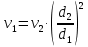  Подставляем и получаем  или или 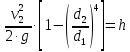 Отсюда  Расход определим по формуле  м3/с. м3/с.Ответ: Q=0,0049 м3/ч. Так как расход зависит от диаметра трубок пьезометров и разностью уровней в них, то перепад h не изменится, если вместо воды в трубе будет протекать нефть при том же расходе. Задача 2.3.2 Вода вытекает из закрытого сосуда с избыточным давлением Ризб под напором h по горизонтальной трубе переменного сечения d1, d2, d3, оканчивающейся вентилем. Определить расход воды Q, построить линии пьезометрического, скоростного и полного напоров. При расчете учесть потери напора на местные сопротивления. Исходные данные Ризб =2,0·105 Па; h = 0,5 м; d1 = 75 мм; d2 = 50 мм; d3 = 25 мм.  Решение Выберем линию сравнения 0-0, проходящую через центр выходного сечения трубопровода. Составим уравнение Бернулли для сечений 0-0 (вход в трубу) и 3-3 (выход в атмосферу из вентиля):  (1) (1)где z0, z3 – геометрический напор в сечении 0-0 и 3-3, соответственно, м; р0, р3 – давление жидкости в сечении 0-0 и 3-3, соответственно, Па; v0, v3 - средняя скорость потока в сечении 0-0 и 3-3, соответственно, м/с; α0, α3- коэффициент Кориолиса в сечении 0-0 и 3-3, соответственно; ρ – плотность воды, кг/м3; ΣhW0-3 – суммарные потери напора между сечениями 0-0 и 3-3 . Геометрическая высота в сечениях z0 =z3= 0. Давления в сечениях: 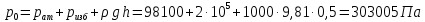 Р3 = рат =98100Па. Плотность воды ρ =1000 кг/м3 . Примем коэффициенты Кориолиса для сечений α0= α3 =1. Скорость потока в сечении 0-0 примем равной нулю v0=0, считая, что жидкость не движется до входа в трубу. С учетом известных величин выразим из уравнения (1) скорость течения жидкости в сечении 3-3 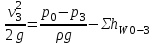 (2) (2)Суммарные потери напора в рассматриваемом трубопроводе складываются из потерь на местных сопротивлениях, т.к. потерями на трение по длине пренебрегают. Тогда можно записать равенство  (3) (3)где hвх0 – местные потери напора на входе в трубу; hвс1, hвс2 – местные потери напора на внезапном сужении в сечениях 1-1 и 2-2; hвых3 – местные потери напора на вентиле. Местные потери напора по формуле Вейсбаха: 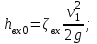 (4) (4) (5) (5)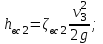 (6) (6) (7) (7)где  = 0,5– коэффициент местного сопротивления входа в трубу из напорного бака; = 0,5– коэффициент местного сопротивления входа в трубу из напорного бака; 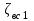 и и  – коэффициент местного сопротивления внезапного сужения трубопровода в сечениях 1-1 и 2-2; – коэффициент местного сопротивления внезапного сужения трубопровода в сечениях 1-1 и 2-2; 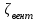 = 5,0 – коэффициент местного сопротивления нормального вентиля; = 5,0 – коэффициент местного сопротивления нормального вентиля; v1 , v2, v3 - скорость течения воды на участке трубопровода с диаметром d1,d2,d3. Коэффициент местного сопротивления при внезапном сужении трубопровода в сечении 1-1   (8) (8)где ωу, ωш-площадь узкого и широкого сечения трубы соответственно. 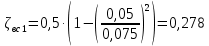 Коэффициент местного сопротивления при внезапном сужении трубопровода в сечении 2-2   (9) (9)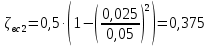 Выразим скорость на участках трубопровода через расход. 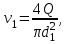 (10) (10) (11) (11)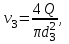 (12) (12)где Q – расход через трубопровод. Учитывая выражения (10-12) выразим скоростной напор на участках трубопровода 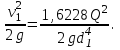 (13) (13) (14) (14) (15) (15)6. Учитывая выражения (11-13) формулу (3) можно записать в виде:  (14) (14)Подставляем (13, 14) в (3) и определяем расчетную формулу расхода воды через трубопровод  (15) (15) Определим скоростной напор на каждом участке по формулам (10-12) 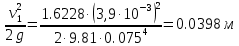   Построим напорную линию для всех участков трубопровода. Напорная линия показывает, как изменяется полный напор по длине трубопровода. Полный напор на входе в трубу (перед сечением 0-0)  (16) (16)Полный напор после входа в трубу(после сечения 0-0)  (17) (17)Полный напор перед сечением 1-1 равен полному напору  , т.к. по условию задачи потери напора на трение не учитываются. Тогда полный напор после сечения 1-1 , т.к. по условию задачи потери напора на трение не учитываются. Тогда полный напор после сечения 1-1  (18) (18)Полный напор после сечения 2-2  (19) (19)Полный напор после сечения 3-3  (20) (20)Построим пьезометрическую линию для всех участков трубопровода. Пьезометрическая линия показывает, как изменяется удельная потенциальная энергия по длине трубопровода. В пределах каждого участка пьезометрическая линия параллельна напорной и ниже ее на величину скоростного напора. Пьезометрический напор на входе в трубу (перед сечением 0-0) равен полному  Пьезометрический напор после входа в трубу  Пьезометрический напор после сечения 1-1 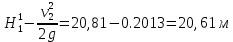 Пьезометрический напор после сечения 2-2  Пьезометрический напор в сечении 3-3 обращается в нуль.  Задача 3.2.1 Вода под постоянным напором Н вытекает в атмосферу через внешний цилиндрический насадок диаметром d. Принимая коэффициент сжатия струи в насадке равным ε=0,63; коэффициент сопротивления входа в насадок ζвх=0,06, определить расход воды. Какими будут при этом вакуум в насадке и потери напора? Потери на трение в насадке не учитывать. Исходные данные Н=5 м; d=20 мм. 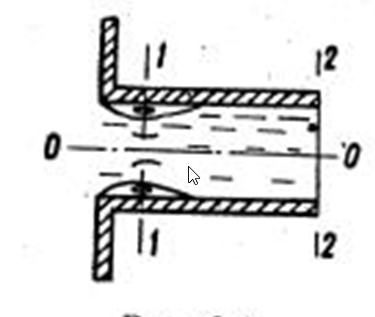 Решение Из уравнения Бернулли, записанного для сечения, совпадающего со свободной поверхностью и сечения 2-2 получаем  Где потери напора включают потери на вход и потери на внезапное расширение   Скорость струи в сжатом сечении при истечении через отверстия и насадки в общем случае определяется по формуле  Коэффициент скорости φ  Скорость истечения 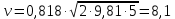 м/с м/сРасход воды через насадок  см3/с см3/сПотери напора в насадке  м, м,что составляет 33,4% от напора Н=5,0 м. Для определения вакуума в насадке рассмотрим уравнение бернулли для сечений 1-1 и 2-2 относительно оси 0-0.  Где р1=р2, α  1, 1,  Отсюда находим  м мЧто составляет 78,2% напора Н=5,0 м. |
