Контрольная работа по методам математической физики. ИКР-Ефимов. Контрольная работа по дисциплине Методы математической физики студент Ефимов С. И. (Оат 1901) Проверил к ф. м н. Завалий М. В
 Скачать 36.57 Kb. Скачать 36.57 Kb.
|
|
Министерство науки и образования Российской Федерации филиал федерального государственного автономного образовательного учреждения высшего образования «Российский государственный университет нефти и газа (национальный исследовательский университет) имени И. М. Губкина» в г. Оренбурге (филиал РГУ нефти и газа НИУ имени И. М. Губкина» в г. Оренбурге) Отделение (автоматизация технологических процессов и производств) Индивидуальная контрольная работа по дисциплине: Методы математической физики Выполнил: студент Ефимов С.И. (ОАТ 19-01) Проверил: к.ф.-м.н. Завалий М. В. Задача 1. Построить функции Грина для внутренней и внешней задач Неймана для шара, круга и полупространства. Решение Шар. Рассмотрим внутреннюю задачу Неймана:  (1) (1)Функция G(M, Q) называется функцией Грина внутренней задачи Неймана для оператора Лапласа, если: 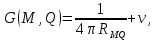 где где  – гармоническая функция в D; – гармоническая функция в D;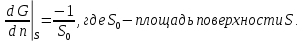 По формуле:   Подставляя функцию Грина в (2), получим выражение для решения задачи (1):  Решение задачи Неймана для шара в форме, найденной самим Нейманом из физических соображений:  Функция G(M, Q) называется функцией Грина оператора Лапласа для внешней краевой задачи в области De, если: 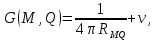 где где  – гармоническая функция в D; – гармоническая функция в D;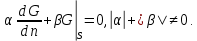  Решение внешней задачи Неймана для шара V дается следующей формулой: 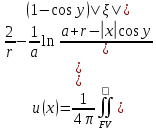 Для круга 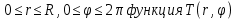 удовлетворяет уравнению удовлетворяет уравнению 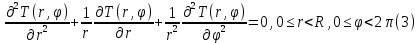 и граничному условию 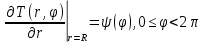 Функция 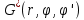 удовлетворяет уравнению удовлетворяет уравнению 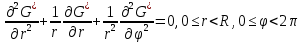 и граничному условию 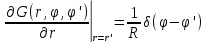 Искомое решение 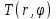 имеет вид (интеграл Дини) имеет вид (интеграл Дини)  Решением внешней задачи (при 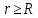 ) для уравнения (3) с граничным условием ) для уравнения (3) с граничным условием   Является интеграл вида 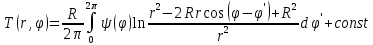 Для полупространства 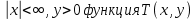 удовлетворяет уравнению Лапласа внутри D удовлетворяет уравнению Лапласа внутри D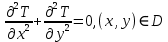 и согласно граничному условию 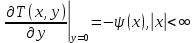 Функция 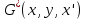 удовлетворяет уравнению и граничному условию удовлетворяет уравнению и граничному условию 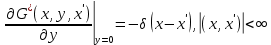 и имеет вид 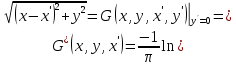  Искомое решение 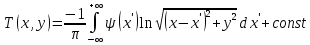 Задача 2. Вычислить объемный потенциал для шара радиуса R с центром в начале координат О с плотностями: 1)  , 2) , 2) 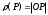 , 3) , 3)  . .Решение: Найдём объёмный потенциал, решая прямым вычислением объемного интеграла. Известно, что объёмный потенциал  где V- объём шара, является функцией, гармонической вне сферы (при r>R), удовлетворяющей уравнению 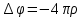 внутри шара и непрерывной вместе с нормальной производной на его границе. Так как ρ0=const, то потенциал обладает сферической симметрией. Данная задача сводится к вычислению объёмного интеграла 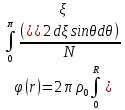 где 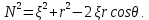 Вводя новую переменную интегрирования N вместо θ и учитывая, что 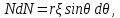 получаем:  Если r > R, то r > ξ всегда и  Если r < R, то 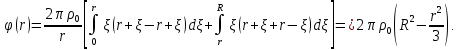 Объёмный потенциал однородного шара φ:  где R - радиус шара, 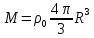 - его масса. - его масса.Список литературы Бабич В.М., Капилевич М.Б., Михлин С.Г. и др. Линейные уравнения математической физики. М.: Наука, 1964. - 368 с. Карташов Э.М. О новом подходе в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа. Инженерный журнал: наука и инновации, 2013, вып. 13. Макаров А.П. Уравнения математической физики. Череповец, 2004 – 175 с. Оренбург-2022 |
