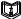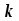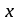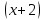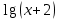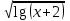Фёдоров ЭО-1-19 4 практика ММИ. Решение для уравнения 1) на отрезке. Говорят, что функция удовлетворяет на отрезке условию Липшица с постоянной, если для любых выполняется неравенство
 Скачать 141.53 Kb. Скачать 141.53 Kb.
|
Кафедра Инженерная кибернетика Отчет по практической работе № 4 Решение систем линейных алгебраических уравнений методом итераций 19 вариант Выполнил(-а): Фёдоров Д.В. студент группы ЭО-1-19 Проверила:Филимонова Т.К. Казань 2021 Решение нелинейного уравнения первого порядка методом итераций Пусть дано нелинейное уравнение с одной неизвестной 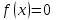 , полагая , полагая 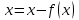 приходим к эквивалентному уравнению: приходим к эквивалентному уравнению: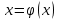 , (3.1) , (3.1)где 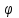 - заданная функция от - заданная функция от 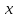 , например , например 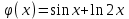 . .Уравнение (3.1) может иметь либо одно решение, либо некоторое конечное число решений (больше одного), либо совсем не иметь решений. Обычно возникают два вопроса: о наличии решений и о том, как найти решение. Требуется найти решение 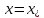 для уравнения (3.1) на отрезке для уравнения (3.1) на отрезке 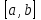 . .Говорят, что функция 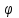 удовлетворяет на отрезке удовлетворяет на отрезке 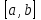 условию Липшица с постоянной условию Липшица с постоянной 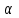 , если для любых , если для любых 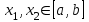 выполняется неравенство выполняется неравенство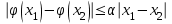 . (3.2) . (3.2)В частности, если функция 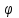 непрерывно дифференцируема на отрезке непрерывно дифференцируема на отрезке 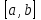 , то она удовлетворяет на , то она удовлетворяет на 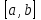 условию Липшица с постоянной условию Липшица с постоянной 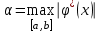 , (3.3) , (3.3)что следует из формулы конечных приращений Лагранжа 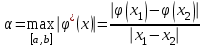 Условия сходимости итераций. Теорема. Пусть функция 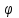 удовлетворяет на отрезке удовлетворяет на отрезке 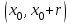 условию Липшица с постоянной условию Липшица с постоянной 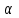 , причем , причем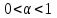 , (3.4) , (3.4)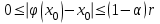 . (3.5) . (3.5)Тогда уравнение (3.1) имеет на отрезке 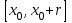 единственное решение единственное решение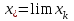 , (3.6) , (3.6)где 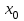 - левый конец отрезка - левый конец отрезка 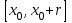 . .Итерационный процесс считается по формуле 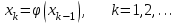 , (3.7) , (3.7)при этом имеют место оценки итераций 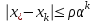 , (3.8) , (3.8)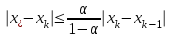 , (3.9) , (3.9)где 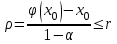 , , Если задано нелинейное уравнение 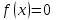 или или 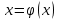 и для и для 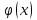 условия (3.4) и (3.5) не выполняются, то преобразуем исходное уравнение условия (3.4) и (3.5) не выполняются, то преобразуем исходное уравнение 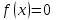 следующим образом: следующим образом: 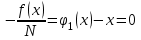 . .Таким образом, берется другая функция, связанная с функцией 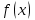 соотношением соотношением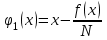 . (3.10) . (3.10)Считая, что 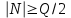 где где 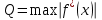 , число , число 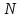 имеет тот же знак, что и имеет тот же знак, что и 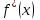 на отрезке на отрезке 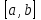 . Снова проверяются условия (3.4) и (3.5) для функции . Снова проверяются условия (3.4) и (3.5) для функции 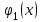 . .Геометрическая интерпретация метода итерации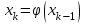 , , 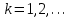 решение 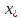 уравнения уравнения 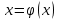 является абсциссой точки пересечения прямой является абсциссой точки пересечения прямой 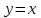 и кривой и кривой 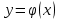 . Сходящиеся итерации приведены на рис. 2.1, 2.2. . Сходящиеся итерации приведены на рис. 2.1, 2.2.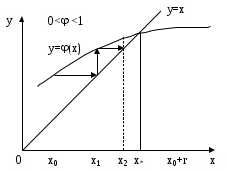 Рис.2.1 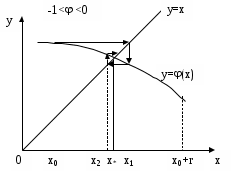 Рис.2.2 y=lgx+3) Геометрически видно, рис.2.1, если в окрестности решения 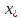 выполняется неравенство выполняется неравенство 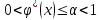 , то последовательность , то последовательность 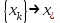 , причем с той стороны, с которой расположено начальное приближение. В случае , причем с той стороны, с которой расположено начальное приближение. В случае 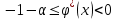 последовательные приближения расположены поочередно с разных сторон. Из рисунков видно, что сходимость тем быстрее, чем меньше последовательные приближения расположены поочередно с разных сторон. Из рисунков видно, что сходимость тем быстрее, чем меньше 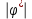 . .Практическое Задание. Решить уравнение 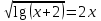 с точностью с точностью 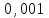 . . Найдем приближенное значение корней графически. Пусть 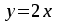 и и 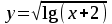 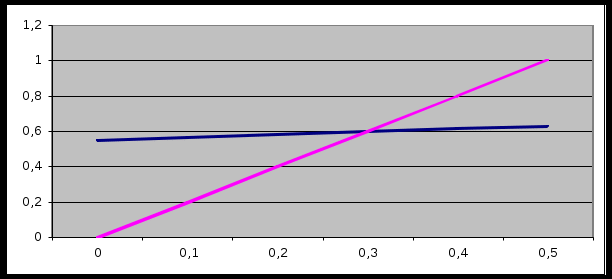 Следовательно, на основании графика выше можно установить, что уравнение 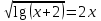 имеет один корень на отрезке имеет один корень на отрезке 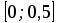 . Для уточнения этого корня используем итерации. Приведем уравнение к виду . Для уточнения этого корня используем итерации. Приведем уравнение к виду 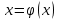 . . Так как 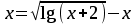 , то , то 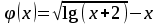 . .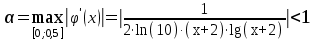 ; ; 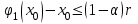 условие (3.4) выполняется, а (3,5) нет, значит необходимо преобразовать исходное уравнение 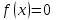 . .Преобразуем исходное уравнение 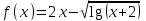 . .Следующим образом 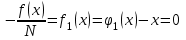 . .Или 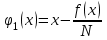 . .Считая, что 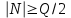 где где 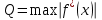 , число , число 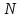 имеет тот же знак, что и имеет тот же знак, что и 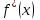 на на 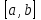 . .Находим 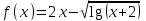 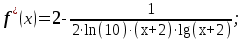 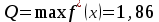 Примем 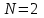 , тогда , тогда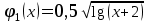 Проверяем условия сходимости итераций (3.4) и (3.5) 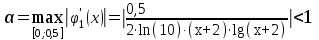 ; ; 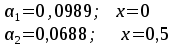 (3.4) (3.4) 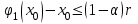 (3.5) (3.5)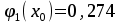 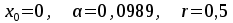 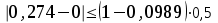 ; ; 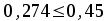 . . Условия сходимости Липшица (3.4) и (3.5) выполняются. Итерацию проведем по формуле (3.7) в таблице 3.1, 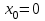 (левый конец отрезка) (левый конец отрезка)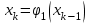 или или 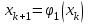 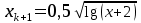 , , 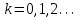 Таблица
Ответ: 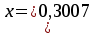 Проверка: 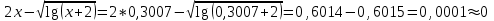 4 и 5 итерации отличаются менее чем 0,001. |