Шпоры по ВМ. Вопрос 10. Вопросы приближения функций. Постановка задачи. Многочлен Ньютона с распределяющими разностями. 8

• Название: Вопрос 10. Вопросы приближения функций. Постановка задачи. Многочлен Ньютона с распределяющими разностями. 8
• Дата: 19.12.2021
• Размер: 1.12 Mb.
• Имя файла: Шпоры по ВМ.doc
• Тип: Решение; #309079
• страница: 1 из 3

ВОПРОС №1. Основные понятия вычислительной математики. 1

ВОПРОС №2. Решение не линейного уравнения методом простейшей итерации. Понятие сжимающего отображения. Теорема о сходимости метода. Геометрическая интерпретация. 3

ВОПРОС №3. Уравнение МПИ. Условие на выбор числа r. Геометрическая интерпретация. 3

ВОПРОС №4. Метод Ньютона для решения не линейного уравнения. Условие сходимости метода. Геометрическая интерпретация. 4

ВОПРОС №5. Метод секущих. Условие сходимости. Геометрическая интерполяция. 4

ВОПРОС №6. Метод Стеффенсена. Условие сходимости. Геометрическая интерполяция. 4

ВОПРОС №7. Методы решения СЛАУ. Прямые и итерационные методы. Условие сходимости итерационных методов. 5

ВОПРОС №8. Метод простой итерации для решения СНУ. Теорема о сходимости методов. 6

ВОПРОС №9. Вопросы приближения функций. Постановка задачи. Понятие точной и интерполяционной аппроксимации. Интерпретационный многочлен Лагранжа. Теорема о единственности. 7

ВОПРОС №10. Вопросы приближения функций. Постановка задачи. Многочлен Ньютона с распределяющими разностями. 8

ВОПРОС №11. Вопросы приближения функций. Постановка задачи. Многочлен Ньютона с конечными разностями для интерполяции вперёд. 8

ВОПРОС №12. Многочлен Ньютона с конечными разностями для интерполяции назад. 9

ВОПРОС №13. Многочлен Ньютона с конечными разностями для интерполяции Сплайны. 10

ВОПРОС №14. Многочлен Ньютона с оконченными разностями для интерполяции. Характер экспериментальных данных. Понятие аппроксимации. Метод выбранных точек и средних. 11

ВОПРОС №15. Метод наименьших квадратов. 12

ВОПРОС №17. Численное интегрирование и дифференцирование. 12

ВОПРОС №18. Общая постановка задачи Коши. Метод Эйлера для её решения. 13

ВОПРОС №19. Общая постановка задачи Коши. Метод Рунге – Кутта для её решения. Метод Рунге – Кутта 4-го порядка точности. 14

ВОПРОС №21. Вычисление собственных чисел матрицы. 15

ВОПРОС №1. Основные понятия вычислительной математики.

Численные методы. Решение подавляющего большинства инженерных и научно-технических задач в настоящее время тесно связано с применением вычислительной техники и основывается на описании реальных процессов математическими моделями, которые представляют собой совокупности обычных, интегральных и дифференциальных уравнений.

Всякая математическая модель представляет собой математическое преобразование вида

Y=F(x,u)

где x = (x1,...,xn) - совокупность входных параметров;

y = (y1,...,yn) - совокупность выходных параметров объекта;

U = (U1,...,Un) - совокупность входных управляющих воздействий, с помощью которых осуществляется управление процессами;

F - оператор преобразования.

Для решения математических задач в САПР применяются три группы методов: графические, аналитические, численные.

Графические методы предполагают искать решение с помощью геометрических построений.

Аналитические методы предполагают искать решение задачи в виде формулы.

Численные методы являются основными методами в САПР. В их основе лежит процедура сведения решения задачи к конечному числу арифметических действий над числами, и получить результат в виде численных значений.

Основные требования и показатели численных методов:

1) устойчивость;

2) сходимость;

3) эффективность (скорость сходимости);

4) погрешность.

Алгоритм считается устойчивым, если он обеспечивает нахождение существующего и единственного решения при различных исходных данных.

Сходимость является основным критерием оценки алгоритма. Алгоритм сходится, если итерационная последовательность приближений.

x¹,x²,...,x^k x^* , k   , т. е.



Скорость сходимости. (эффективность) – обозначает количество итераций, затраченных алгоритмом для достижения приемлемой точности решения задачи. Сущ. 3 оценки скорости сходимости: линейная и сверх линейная. Пусть x^kx^* , k  

Говорят, что алгоритм обладает линейной скоростью сходимости, если g э [0;1] и R0

|x^k+1-x^*|g_k |x^k-x^*| , при kk₀

Алгоритм обладает сверх линейной скоростью сходимости, если выполняется условие

|x^k+1-x^*|g_k |x^k-x^*| , g 0 , k  

Алгоритм обладает квадратичной скоростью сходимости, если

|x^k+1-x^*|c |x^k-x^*| , c 0

ВОПРОС №2. Решение не линейного уравнения методом простейшей итерации. Понятие сжимающего отображения. Теорема о сходимости метода. Геометрическая интерпретация.

Алгоритмы решения нелинейного уравнения. Метод итераций.

Пусть требуется решить уравнения вида f(x)=0 (*), где f(x) - непрерывная функция.

Чтобы методом итераций найти решение уравнения (*) его необходимо преобразовать к виду

x⁽¹⁾ = (x⁽⁰⁾) (**)

Зададим начальное приближение x₀ и подставим его в правую часть уравнения (**).

Получим значение х₁

Подставив значение х₁ в правую часть уравнения (**) получим х₂

Продолжая этот процесс, неограниченно получим последовательность приближений к корню

x^k+1=(x^k) , k 0 (***)

Условие сходимости метода. Теорема. Пусть в некоторой  - окрестности корня х^* функция (x) непрерывна и дифференцируема и удовлетворяет неравенству | ' (x)| g, (5) где 0 < g < 1 - константа. Тогда независимо от выбора начального приближения х⁽⁰⁾ из указанной  - окрестности корня итерационная последовательность не выходит из этой окрестности и справедлива следующая оценка погрешности: Неравенство (5) означает, что метод простой итерации обладает линейной скоростью сходимости.

Геометрическая интерпретация метода. На рис.1 (а) видно, что корень уравнения (1) является абсциссой точки пересечения графиков двух функций y = x и y =  (x). В случаях (а) и (б) метод простой итерации сходится при произвольном начальном приближении. В случаях (в) и (г) метод расходится при любом начальном приближении. Замечено, что в случаях (а) и (б)    (x)  < 1, а в случаях (в) и (г)    (x)  > 1.

Сжимающее отображение. Понятие с.о. позволяет решать вопрос о сходимости итерационного процесса аналитически, а не геометрическими построениями. Возьмем непрерывную  (x), заданную на отрезке  a; b . Каждой т. x   a; b соответствует y =  (x ) на оси ординат.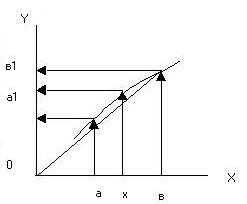

Т.е. функция  (x) задает отображение отрезка  a; b на оси ординат. Чтобы сравнить образ отрезка с самим отрезком необходимо отобразить точки на оси 0y через прямую y = x на ось 0x. Если образ отрезка  a; b  является частью  a; b , то  (x) отображает  a; b в себя. Построим последовательность  a; b ;  a ; b  ;  a ; b  и т.д. Если после каждого отображения отрезок уменьшается в М>1 раз, то отображение называется сжимающим.

Расстояние между двумя т. x1 и x2 =  x2 - x1  . Условие сжатия формулируется: отображение  (x) является сжимающим на отрезке  a; b , если существует 0
  (x2 ) -  (x1 )    x2 - x1  ,  = 1/М.

ВОПРОС №3. Уравнение МПИ. Условие на выбор числа r. Геометрическая интерпретация.

Модификация итерационного процесса.

Применение метода итераций x =(x); часто затрудняется тем, что  (x) несжимающая функция. Помимо этого можно потребовать увеличение скорости сходимости.

Рассмотрим исходное уравнение

f (x) = 0, (1) где f (x) =  (x) – x. Решение x итерационного процесса будет и решением (1).

Преобразуем (1) следующим образом f (x) = 0  r f (x) = 0  x = x + r f (x) или x =  (x) (2)

где f (x) = x + r f (x), r  0.

Итерационный процесс происходит по формуле

x =  (x ) или x = x + r f (x ),  = 0,1,2, ... (3)

Решение (2) является решением (1).

В предложенном варианте существование решения и сходимость x , x , x , ... , x , ... обеспечивается условиями теоремы сжатия относительно  (x). При этом r может быть выбрана таким методом, что условие сжатия выполняется для  (x) в тех случаях, когда  (x) несжимаема.

Пусть    (x)  >1 для итерационного процесса x =  (x). Будем искать решение (1) решая (2) с помощью алгоритма (3), а число r выберем из условия сжатия для  (x) при x = x*.

   (x*) < 1, или  1+ r f  (x*) < 1,  1+ r(  (x*) – 1)  < 1 (4)

-1<1+ r(  (x*) – 1) < 1 

 -2< r(  (x*) – 1) < 0

 -2/  (x*) – 1< r< 0,

r< 0 и  r < 2 /  (x*) – 1, если   - 1> 0

r> 0 и  r < 2 /  (x) – 1, если   - 1> 0

Из условия сжатия функции  (x) получим рекомендации для выбора числа r в уравнении (2) и алгоритма (3), обеспечивающих сходимость (3). Можно потребовать наиболее сильного сжатия,   (x*) = 0 (5) Отсюда получаем значение r = -1/   (x*) – 1 (6)

Геометрическая интерпретация.

Касательная в т. Bn y – f(x ) = f (x )(x-xn ).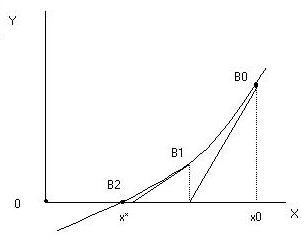



ВОПРОС №4. Метод Ньютона для решения не линейного уравнения. Условие сходимости метода. Геометрическая интерпретация.

Метод Ньютона. В предложенной методике есть недостаток: r = const на протяжении всего процесса поиска корня. Однако нет препятствий для изменения этого значения в процессе выполнения итерационного процесса. Сделаем r функцией x и подставим в алгоритм:

x = x + r(x ) f (x ), n = 0,1,2, ... .(7)

Потребуем, чтобы   (x) была = 0 в достаточно большой окрестности корня x*:

  (x) = 1 + r f  (x) = 0,

отсюда r(x) = -1/ f  (x) = -1/  (x) –1.

Тогда алгоритм будет иметь вид:

x(n+1) = x^(к) - f(x^(к)) / f  (x^(к)) – метод Ньютона.

Условие сходимости метода. Для вывода сходимости метода потребуем сжатия функции (x)=x-f(x) / f ‘(x) на произвольном отрезке: x ∊ [a;b]. Если ф-я f(x) – сжимающая, то для люб. x₀, x₁ из отрезка [a;b] должно происходить уменьшение длины (x₁ – x₀) при каждом новом отображении ф-и (x). Запишем условие сжатия след. образом: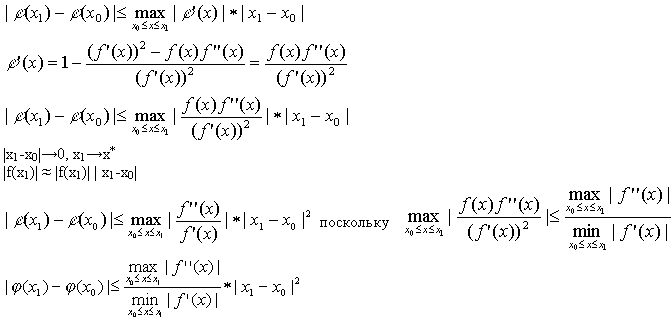



В ф-ле сжимающегося отобр-я x<1 отсюда если вып. M/m*|x₁-x₀|<1, то метод сходится. |x^k+1-x^*|  M / m |x^k-x^*|²

Геометрическая интерпретация.

Касательная в т. Bn y – f(x ) = f (x )(x-xn ).




ВОПРОС №5. Метод секущих. Условие сходимости. Геометрическая интерполяция.

М 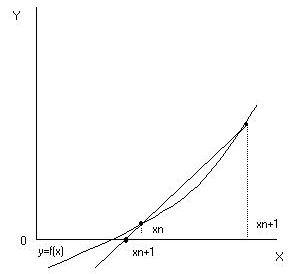етод секущих. Полагая y = 0, x = xn+1 получим формулу для метода Ньютона. Если значения производной вычислять приближенно, как приращение f(x) в т. x и xn-1, то получим метод секущих.



При условии x = x и y(x) = 0 получим (1).

Оценка скорости сходимости (***).

Условие сходимости метода. Для вывода сходимости метода потребуем сжатия функции (x)=x-f(x) / f ‘(x) на произвольном отрезке: x ∊ [a;b]. Если ф-я f(x) – сжимающая, то для люб. x₀, x₁ из отрезка [a;b] должно происходить уменьшение длины (x₁ – x₀) при каждом новом отображении ф-и (x). Запишем условие сжатия след. образом: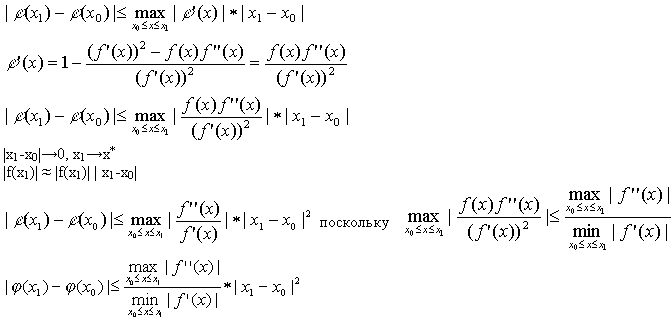



В ф-ле сжимающегося отобр-я x<1 отсюда если вып. M/m*|x₁-x₀|<1, то метод сходится. |x^k+1-x^*|  M / m |x^k-x^*|²


ВОПРОС №6. Метод Стеффенсена. Условие сходимости. Геометрическая интерполяция.

Метод Стеффенса. В формулу метода Ньютона сделаем замену f  (x )  f(z ⁿ ) - f(x ⁿ )/ z ⁿ - x ⁿ при условии z ⁿ  x ⁿ и следует из определения производной f  (x ) = lim z x f(z)-f(x)/z-x.

Заменив z ⁿ = x ⁿ + f(x ⁿ ), x ⁽ⁿ⁺¹⁾ = x ⁿ - f²(x ⁿ )/ f(x ⁿ + f(x ⁿ ))- f(x ⁿ ), n  0.

Г 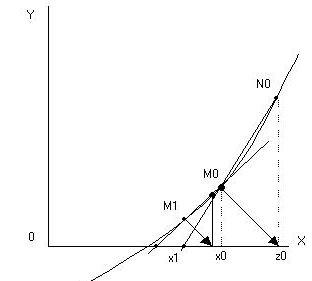еометрическая иллюстрация.

Приближение x ⁿ получается как абсцисса т. пересечения с 0 x секущей, проходящей через т. М ⁿ и N ⁿ c координатами (x ⁿ , f(x ⁿ)) и (z ⁿ , f(z ⁿ )).Значение z ⁿ соответствует абсциссе т. пересечения с осью 0x прямой y = f(x ⁿ ) – (x - x ⁿ ), проходящей через т. Мⁿ и параллельной прямой y = - x.

ВОПРОС №7. Методы решения СЛАУ. Прямые и итерационные методы. Условие сходимости итерационных методов.

Численные методы линейной алгебры. К численным методам линейной алгебры относятся численные методы решения систем линейных алгебраических уравнений, обращения матриц, вычисления определителей и нахождения собственных значений и собственных векторов матриц.

Методы решения систем ЛАУ разбиваются на две группы. К первой группе точные или прямые методы – алгоритмы, позволяющие получить решение системы за конечное число арифметических действий. К этой группе относится метод Гаусса.

Вторую группу составляют приближенные методы (итерационные) решения СЛАУ.

Метод Гаусса Предназначен для решения СЛАУ вида:



или Ах=в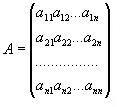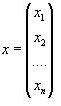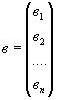

, ,

Предположим, что матрица А - невырожденная, т.е. det А не равно 0. В этом случае решение системы существует и оно единственно, а рассматриваемая задача корректна.

Вычисления с помощью метода Гаусса. Состоят из двух шагов, называемых прямым и обратным ходом. Прямой ход метода Гаусса заключается в последовательном исключении неизвестных из системы с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода. Рассмотрим простейший вариант метода Гаусса, называемый схемой единственного деления. Прямой ход состоит из (n-1) шагов исключения.

1-й шаг. Целью этого шага является исключение неизвестного x₁ из уравнений с номерами i = 2,3,...,n. Предположим, что коэффициент a₁₁  0 (главный элемент первого шага)

Вычислим величины _i1=a_i1 /a₁₁(i=2,3,...,n), называемые множителями 1-го шага. Вычтем из второго, третьего и ... до n-го уравнений системы (1) первое уравнение, умноженное соответственно на  ₂₁,₃₁,..., _n1.Это позволит обратить в нуль коэффициенты при х₁ во всех уравнениях , кроме первого. В результате получим эквивалентную систему.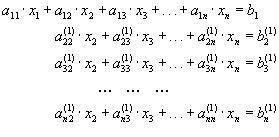



в которой a_ij⁽¹⁾=a_ij-_i1 a_ij , b_i⁽¹⁾=b_i-_i1 b₁.

2-й шаг. На этом шаге производится исключение х₂ из уравнений с номерами i = 3, 4, . . . , n.

Вычислим _i2=a_i2⁽¹⁾/ a₂₂⁽¹⁾ относительно главного элемента 2-го шага, после чего произведем те же действия по исключению элементов а_i2 из 3-й n . . . строк.

Аналогично проводятся остальные шаги.

k-й шаг. Предположим, что главный элемент k-го шага a_kk^(k-1)0, вычислим множители k-го шага
_ik= a_ik^(k-1)/a_kk^(k-1) , (i=k+1,...,n) и вычтем последовательно из (k + 1)-го , . . . , n-го уравнений полученной на предыдущем шаге системы k-е уравнение, умноженные соответственно на  _k+1,_k+2,..., _nk.

После (n -1) - го шага исключения получим систему уравнений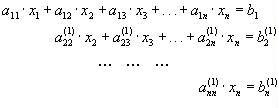

(2)

Получается матрица А^(n-1), которая является верхней треугольной. На этом вычисления прямого хода заканчиваются.

Обратный ход. Из последнего уравнения системы (2) вычислим х_n. Подставляя полученное значение в предпоследнее уравнение, вычислим значение х_n-1. Таким образом, можно вычислить значения всех неизвестных. Вычисления здесь проводятся по формулам:





Метод простой итерации.

Для того чтобы применить метод простой итерации к решению системы ЛАУ

Aх = b (3)

С квадратной невырожденной матрицей А, необходимо преобразовать эту систему к виду

х = Вх + с, (4)

где В - квадратная матрица с элементом b_ij (i,j=1.n), с - вектор столбец с элементами c_i (i=1,n).

Зададим некоторое начальное приближение x⁽⁰⁾=(x₁⁽⁰⁾,x₂⁽⁰⁾,..., x_n⁽⁰⁾)^T. Подставив его в правую часть системы (4), находим первое приближение x₍₁₎= Bx₍₀₎+c и так далее.

Сходимость метода простой итерации.

||B||<1. В этом случае существует и единственное решение системы (3) x. При этом метод итерации сходится при произвольном начальном приближении x⁽⁰⁾.

||B|| - норма матрицы.

Евклидова норма матрицы, имеет вид: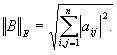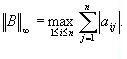



Критерий окончания итерационного процесса.

||x⁽ⁿ⁾-x^(n-1)|| < 

Метод Зейделя.

Пусть система (3) приведена к виду: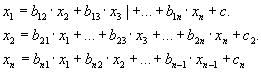



С коэффициентами, вычисленными по формулам:

в_ij = - a_ij / a_ii , c_ij = в_i / a_ii (i,j = 1,n , j i)

Метод Зейделя представляет собой модификацию метода простых итераций. Идея метода состоит в том, что при вычислении на (k+1)-ом шаге приближения к неизвестному х_i при i>1, используется уже найденное (k+1)-е приближение x ₁ , x ₂, . . . , x _i-1

Таким образом матрица В разбивается на две треугольные матрицы: верхнюю и нижнюю.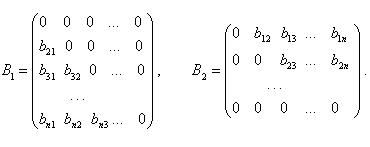



Расчетная формула принимает вид:

x ^k+1 =B₁ x ^k+1 + x ^k + C

или



Условия сходимости и критерий окончания итерационного процесса те же.
ВОПРОС №8. Метод простой итерации для решения СНУ. Теорема о сходимости методов.

Методы решения систем нелинейных уравнений.

f₁ (x₁, x₂, . . . , x_n) =0,

f₂ (x₁, x₂, . . . , x_n) =0,

..........

f_n (x₁, x₂, . . . , x_n) =0,

Найти точное решение системы (1), то есть вектор x = (x₁, x₂, . . . , x_n)^T удовлетворяющий уравнениям (1), практически невозможно, так как в описанном случае исключается использование прямых методов. Реальным путем решения системы (1) является использование итерационных методов для получения приближенного решения x^* = (x₁^*, x₂^* , . . . , x_n^*) удовлетворяющего при заданном  > 0 неравенству ||x^* - x|| < .

Для удобства будем использовать сокращенную векторную форму записи систем: вектор неизвестных x = (x₁, x₂, . . . , x_n)^T и векторную функцию f = (f₁, f₂, . . . , f_n)^T.

В этих обозначениях система (1) примет вид:

f (x) = 0. (2)

Метод релаксации.

Имеем систему: Преобразуем ее к виду: Зададим начальное приближение: x⁽⁰⁾=(x₁⁽⁰⁾, x₂⁽⁰⁾,...,x_n⁽⁰⁾)

и 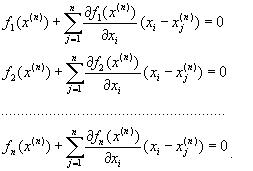подставим в полученную систему.
Получаем невязки (отклонения).

Если одной из неизвестных x_s⁽⁰⁾ задать приращение  x_s⁽⁰⁾, то соответствующая невязка уменьшится на эту величину, а все остальные невязки R_i⁽⁰⁾(iS) увеличатся на величину b_is x_s⁽⁰⁾.то есть, чтобы обратить очередную невязку R_s⁽¹⁾ в нуль, необходимо величине x_s⁽⁰⁾ дать приращение  x_s⁽⁰⁾= R_s⁽⁰⁾ и получим R_s⁽¹⁾=0 и R_i⁽¹⁾= R_i⁽⁰⁾ + b_is x_s⁽⁰⁾.

Таким образом, идея метода состоит в том, чтобы на каждом шаге обращать в нуль максимальную по модулю невязку путем изменения значения соответствующей компоненты приближения. Процесс заканчивается, когда все невязки последней преобразованной системы будут равны нулю с заданной точностью.

Будем считать функции f_i(x), входящие в систему (1) непрерывно дифференцируемыми в некоторой окресности решения x¯. Введем для системы функций f₁,f₂,...,f_n матрицу Якоби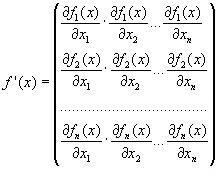

( 3)

Метод простой итерации.

Преобразуем систему (1) к эквивалентному виду: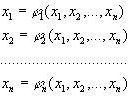

(4)

Зададим начальное приближение x⁽⁰⁾= (x1⁽⁰⁾,x2⁽⁰⁾,...,xn⁽⁰⁾. Подставляя его в правую часть системы (4) получим первое приближение к решению. Повторяя этот процесс решения системы (1). Очередное приближение x^(k+1)вычисляется по формулам

Е 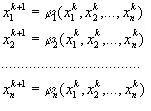сли ввести в рассмотрение векторную функцию  =(₁,₂, ...,_n), то итерационный процесс можно записать кратко

x^(k+1)=(x^(k)). (5)

По аналогии с МПИ для решения одного нелинейного уравнения рассмотрим условия работоспособности МПИ для СНУ.

Сходимость метода.

Пусть '(x) - матрица Якоби, отвечающая вектор - функции (x).

Теорема. Пусть в некоторой  - окрестности решения x¯ функции _i(x) (i=1,n¯) дифференцируемы и выполнено неравенство

||'(x)||g, где 0g<1 (const).

Тогда независимо от выбора начального приближения x⁽⁰⁾ из указанной -окрестности корня итерационная последовательность не выходит из этой окрестности, метод сходится со скоростью геометрической прогрессии и справедлива следующая оценка погрешности:



На практике часто используется следующая оценка окончания итерационного процесса:

||x⁽ⁿ⁾-x^(n-1)|| ₁

Метод Ньютона для решения СНУ.

Обобщим метод Ньютона для решения одного НУ на решение системы НУ (1).

Предположим, что исходя из начального приближения x⁽⁰⁾ к решению x¯ построены приближения x⁽¹⁾, x⁽²⁾,...,x⁽ⁿ⁾.Заменим в системе (1) каждую функцию f_i (i=1,n¯)линейной частью ее разложения по формуле Тейлора в точке x⁽ⁿ⁾: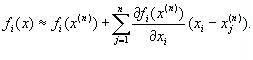



В результате данного преобразования перейдем к СЛАУ

имеющей в матричной форме следующий вид:



где f - матрица Якоби.

Предположим, что матрица Якоби невырожденная, то есть существует обратная матрица



Тогда система (6) имеет единственное решение, которое принимается за очередное приближение x^(k+1) к решению x, то есть приближение x^(k+1) удовлетворяет равенству



выразив из полученного равенства x^(k+1), получим формулу метода Ньютона:







где A_ij - алгебраическое дополнение элемента a_ij.



M_ij - минор элемента a_ij , то есть определитель порядка n - 1, получающийся из A вычеркиванием i - ой строки и j - го столбца.

Сходимость метода.

Теорема. Пусть в некоторой окрестности решения x системы (1) функции f₀(i=1,n) дважды непрерывно дифференцируема и матрица f (x) невырождена. Тогда найдется такая малая ... -окрестность решения x, что при произвольном выборе начального приближения x⁽⁰⁾ из этой окрестности, итерационная последовательность метода Ньютона не выходит за пределы окрестности и справедлива оценка:



метод сходится с квадратичной скоростью.

Критерий окончания процесса.





ВОПРОС №9. Вопросы приближения функций. Постановка задачи. Понятие точной и интерполяционной аппроксимации. Интерпретационный многочлен Лагранжа. Теорема о единственности.

Приближение функций. Постановка задачи. Если величина y является функцией аргумента x, то любому значению x из области определения y будет поставлено в соответствие значение y. Однако, на практике часто неизвестна явная зависимость y от x, то есть ее невозможно записать в виде y = f(x). Бывают случаи, когда затруднительно использовать даже известную зависимость f(x).

Наиболее распространенным случаем, когда вид связи между параметрами y и x неизвестен, является задание этой зависимости в виде таблицы {x_i,y_i}. В этом случае дискретному множеству значений аргумента соответствует множество значений функции {y_i}, i = 1,n. Эти значения получены либо в результате расчетов, либо в результате экспериментов.

Нам могут потребоваться значения функции y и в других точках, = x_i. Однако получить их можно лишь путем сложных расчетов или дорогостоящих экспериментов

Таким образом, мы приходим к необходимости использования имеющихся табличных данных для приближенного вычисления значения y при любом значении параметра x, так как точная связь y = f(x) неизвестна.

Этой цели служит задача аппроксимации функции: функцию f(x) требуется приближенно заменить некоторой функцией ...(x) так, чтобы отклонение ...(x) от f(x) в заданной области было наименьшим. Функция ...(x) при этом называется аппроксимирующей.

Для практики весьма важен случай аппроксимации функции многочленом:



В дальнейшем будем рассматривать только такую аппроксимацию. При этом коэффициенты a_i будут подбираться так, чтобы достичь наименьшего отклонения многочлена от данной функции.

Если приближение строится на заданном дискретном множестве точек {x_i}, то аппроксимация называется точечной. При построении приближения на непрерывном множестве точек аппроксимация называется непрерывной (интегральной).

Точечная аппроксимация.

Одним из основных типов точечной аппроксимации является интерполяция. Она состоит в следующем: для заданной функции y = f(x) строится многочлен, принимающий в заданных точках x_i те же значения y_i, что и функция f(x), то есть



При этом предполагается, что среди значений x_i нет одинаковых, то есть x_i = x_j при i = j. Точки x_i называются узлами интерполяции, а многочлен ...(x) - интерполяционным многочленом.

Таким образом, близость интерполяционного многочлена к заданной функции состоит в том, что их значения совпадают на заданной системе точек.

Максимальная степень интерполяционного многочлена m = n; в этом случае говорят о глобальной интерполяции, так как один многочлен



используется для интерполяции функции f(x) на всем рассматриваемом интервале изменения аргумента x_i . Коэффициенты a_j многочлена находятся из системы уравнений y_i=...(x_i, i = 1,n). При x_i = x_j ( i = j ) эта система имеет единственное решение.

Как правило, интерполяционные многочлены используются для аппроксимации функции в промежуточных точках между крайними узлами интерполяции, то есть при x₀ < x < x_n.

Однако, иногда они используются для приближенного вычисления функции вне рассматриваемого отрезка Этот вид аппроксимации называют экстраполяцией.

К ак видно, при интерполировании основным условием является прохождение графика интерполяционного многочлена через данные значения функции в узлах интерполяции. Однако, в ряде случаев, выполнить данное условие затруднительно или нецелесообразно.

Например, при большом количестве узлов интерполяции получается высокая степень многочлена. Кроме того, исходные данные могут содержать ошибку. Построение аппроксимирующего многочлена, с условием обязательного прохождения его графика через узлы интерполяции, означает повторение имеющейся ошибки. Выходом является исполнение аппроксимальной зависимости, график которой проходит "близко" от узлов интерполяции.

Многочлен Лагранжа.

Перейдем к случаю глобальной интерполяции, то есть построению интерполяционного многочлена, единого для всего отрезка [x₀, x_n]. При этом график интерполяционного многочлена должен проходить через все заданные точки.

Запишем искомый многочлен в виде:



Из условий равенства значений этого многочлена в узлах x_i соответствующим заданным табличным значениям y_i, получим систему уравнений для нахождения коэффициентов a₀, a₁,...,a_n: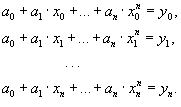



Эта система имеет единственное решение, если среди узлов интерполяции нет совпадающих, то есть, если x_i x_j при i j. Решив эту систему, найдем коэффициенты интерполяционного многочлена. Заметим, что такой путь построения многочлена может потребовать больших вычислений, особенно при большом числе узлов.

Рассмотрим более простой алгоритм построения интерполяционных алгоритмов. Будем искать многочлен в виде линейной комбинации множеств степени n.



При этом потребуем, чтобы каждый многочлен l_i (x)=0 во всех узлах интерполяции, за исключением одного (j-го), где он = 1. Легко проверить, что этим условиям отвечает многочлен вида:



Действительно, l₀(x) = 1 при x = x₀. При x = x₁, ... , x_n числитель выражения = 0. По аналогии получим: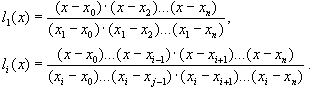



Подставив эти формулы в исходный многочлен получим:



Эта формула называется интерполяционным многочленом Лагранжа.

Докажем, что этот многочлен является единственным. Допустим противоположное: пусть существует еще один многочлен F(x) степени n, принимающий в узлах интерполяции заданные значения, то есть F(x_i) = y_i, i = 0,n. Так как F(x_i) = y_i и L(x_i) = y_i, то разность R(x) = L(x) - F(x), являющаяся многочленом степени n (или ниже), в узлах x_i равна:



Если R(x)=L(x)-F(x) 0, то разность R(x) (будучи многочленом не выше n-й степени- это следует из вида многочлена L(x), в котором n+1 слагаемое, каждое по n множителей), в силу основной теоремы высшей алгебры имеет не более n корней.

[Основная теорема алгебры: каждое алгебраическое уравнение n-й степени



коэффициенты, которого a₁,a₂,...,a_n - действительные или комплексные числа, имеет ровно n корней действительных или комплексных.]

Это противоречит равенствам:

число, которых равно n + 1 (система из (n+1)-го уравнения).

Возникло противоречие: многочлен, который не может иметь более n корней, имеет n+1 корень. Следовательно, многочлены L(x) и F(x) тождественны (L(x) F(x)).

Из формулы интерполяционного многочлена Лагранжа



можно получить выражения для линейной и квадратичной интерполяции: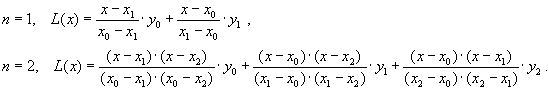



ВОПРОС №10. Вопросы приближения функций. Постановка задачи. Многочлен Ньютона с распределяющими разностями.

Приближение функций. Постановка задачи. (ВОПРОС №9)

Многочлен Ньютона с распределенными разностями.

Пусть некоторая функция f(x) задана таблицей своих значений {x_i;f(x_i} с произвольным размещением узлов интерполяции.

Разделенными разностями первого порядка принято называть величины:



Разделенные разности второго порядка можно вычислить по формуле:



Т.о, разделение разности k-го порядка можно найти по формуле: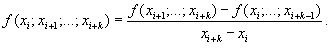



Составим таблицу распределенных разностей: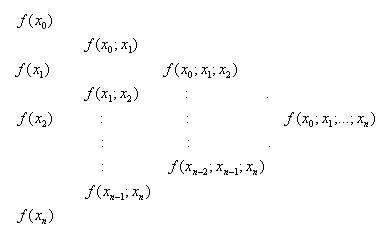



Разделительные разности обладают след. св-ми:

Свойства разделенных разностей.

1). разделительная разность f ( x_i; x_i+1;x_i+k ) является симметричной функцией своих аргументов x_i,x_i+1,x_i+k (не изменяется относительно любой их перестановки);

2). пусть функция f (x) на отрезке [a;b], содержащем точки x_i,x_i+1,x_i+k, производную порядка k. В этом случае:



Любая функция, непрерывная на [a;b] и имеющая на этом отрезке производные, включая k-ю, может быть разложена в ряд Тейлора:



Используя свойства распределенных разностей запишем интерполяционный многочлен Ньютона с распределенными разностями:


ВОПРОС №11. Вопросы приближения функций. Постановка задачи. Многочлен Ньютона с конечными разностями для интерполяции вперёд.

Приближение функций. Постановка задачи. (ВОПРОС №9)

Многочлен Ньютона с конечными разностями для интерполяции вперёд.

В рассмотренных выше методах не делалось никаких предположений о законе распределения узлов интерполяции. Рассмотрим случай равноотстоящих узлов интерполяции, то есть x_i - x_i-1 = const = h, i=2n. h - называется шагом.

Введем понятие конечных разностей. Пусть известны значения функции в узлах x_i : y_i = f(x_i ). Составим разности значений функции: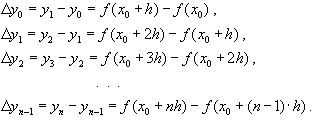



Эти разности называются разностями первого порядка.

Можно составить разности второго порядка:



Аналогично составляются разности k-го порядка:



Выразим конечные разности непосредственно через значение функции: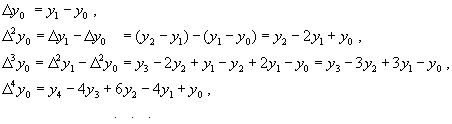



Таким образом, для любого k можно записать:



Запишем эту формулу для значений разности в узле x_i:



Используя конечные разности можно определить



Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в виде:



График многочлена должен проходить через заданные узлы, то есть N(x_i) = y_i(i = 0,n). Используем эти условия для нахождения коэффициентов многочлена: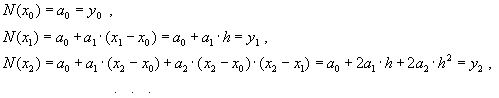



Найдем отсюда коэффициенты a_i :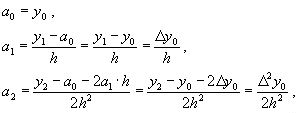



Таким образом для любого k-го коэффициента формула примет вид:



Подставляя эти формулы в выражение многочлена Ньютона получим его следующий вид:



Конечные разности рассчитываются по приведенным выше формулам.

Полученную формулу можно записать в другом виде. Для этого введем переменную



В этом случае: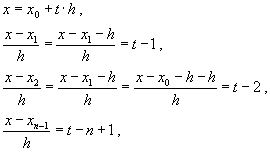



С учетом этих соотношений формулу многочлена Ньютона можно записать в виде:



Полученное выражение может аппроксимировать данную функцию y = f(x) на всем отрезке изменения аргумента [x₀, x_n]. Однако, более целесообразно (с точки зрения повышения точности расчетов и уменьшения числа слагаемых в полученной формуле) ограничиться случаем t < 1, то есть использовать эту формулу для x₀, x, x₁. Для других случаев вместо x₀ принять x_i, если x_i x x_i+1 при i = 0,n-1. В этом случае интерполяционный многочлен можно записать в виде:



Полученная формула называется первым интерполяционным многочленом Ньютона для интерполяции вперед.

Эту интерполяционную формулу обычно используют для вычисления значений функции в точках левой половины рассматриваемого отрезка. Это объясняется следующим: разности

вычисляются через значения функции y_i, y_i+1, ... , y_i+k, причем i + k < n. Из-за этого при больших значениях i мы не можем вычислить разности высших порядков (k < n-i).