Шпоры по ВМ. Вопрос 10. Вопросы приближения функций. Постановка задачи. Многочлен Ньютона с распределяющими разностями. 8

• Название: Вопрос 10. Вопросы приближения функций. Постановка задачи. Многочлен Ньютона с распределяющими разностями. 8
• Дата: 19.12.2021
• Размер: 1.12 Mb.
• Имя файла: Шпоры по ВМ.doc
• Тип: Решение; #309079
• страница: 2 из 3

ВОПРОС №12. Многочлен Ньютона с конечными разностями для интерполяции назад.

В рассмотренных выше методах не делалось никаких предположений о законе распределения узлов интерполяции. Рассмотрим случай равноотстоящих узлов интерполяции, то есть x_i - x_i-1 = const = h, i=2n. h - называется шагом.

Введем понятие конечных разностей. Пусть известны значения функции в узлах x_i : y_i = f(x_i ). Составим разности значений функции: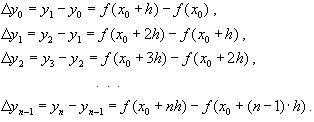



Эти разности называются разностями первого порядка.

Можно составить разности второго порядка:



Аналогично составляются разности k-го порядка:



Выразим конечные разности непосредственно через значение функции: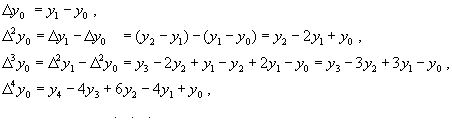



Таким образом, для любого k можно записать:



Запишем эту формулу для значений разности в узле x_i:



Используя конечные разности можно определить



Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в виде:



График многочлена должен проходить через заданные узлы, то есть N(x_i) = y_i(i = 0,n). Используем эти условия для нахождения коэффициентов многочлена: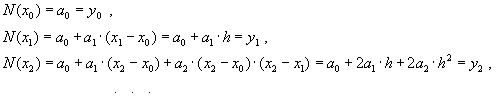



Найдем отсюда коэффициенты a_i :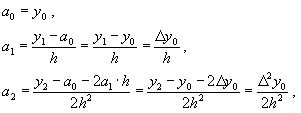



Таким образом для любого k-го коэффициента формула примет вид:



Подставляя эти формулы в выражение многочлена Ньютона получим его следующий вид:



Конечные разности рассчитываются по приведенным выше формулам.

Полученную формулу можно записать в другом виде. Для этого введем переменную



В этом случае: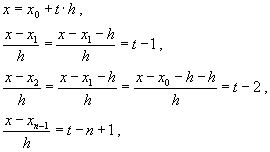



С учетом этих соотношений формулу многочлена Ньютона можно записать в виде:



Полученное выражение может аппроксимировать данную функцию y = f(x) на всем отрезке изменения аргумента [x₀, x_n]. Однако, более целесообразно (с точки зрения повышения точности расчетов и уменьшения числа слагаемых в полученной формуле) ограничиться случаем t < 1, то есть использовать эту формулу для x₀, x, x₁. Для других случаев вместо x₀ принять x_i, если x_i x x_i+1 при i = 0,n-1.

Для правой половины рассматриваемого отрезка разности лучше вычислять справа налево. В этом случае t = (x - x_n ) / h, то есть t < 0 и интерполяционный многочлен Ньютона можно получить в виде:



Полученная формула называется вторым интерполяционным многочленом назад.

ВОПРОС №13. Многочлен Ньютона с конечными разностями для интерполяции Сплайны.

Использование многочленов высокой степени при решении задачи интерполяции связана с повышением сложности вычислений. Помимо этого необходимы спец методы составления подобных многочленов. Дополнительная трудность составляет накопление ошибок в округлении при проведении вычислений. Выходом может служить применение локальной интерполяции с использованием многочленов невысокой степени. Главным недостатком здесь явл. отличие производных у соседних многочленов в т. стыка. Иногда быв. ситуации, требующие гладкости интерполяции многочлена. В этом случае в качестве интерполяции ф-и рекомендуют исп. сплайны, представленные собой спец образом построенные гладкие кусочно-многочленные ф-и, сочетающие в себе локальную простату и глобальную на всём отрезке [x₀; x_n] гладкость. Пусть отрезок [x₀; x_n] разбит на n частей [x_i-1; x_i]. Тогда сплайном степени m Sm(x) наз. ф-ия, обладающая след. св-ми: 1. ф-ия Sm(x) непрерывна на всём отрезке от [x₀; x_m] вместе со своими производноми до некоторого порядка Р; 2. На каждом отрезке [x_i-1; x_i] сплайн совпадает с некоторым многочленом степени m. S_m(x)=P_m,i(x)

Разность теорем между степенью сплайна и наивысшей на отрезке (x₀; x_n) непрерывной производной наз. дефектом сплайна. Показанный на рисунке. Дефект сплайна = 1.

На практике наиб. распространенные полиномы кубич. сплайны с дефектом 1или 2. На каждом отрезке такой сплайн совпад. с полиномом вида:

Потребуем, чтобы на отрезке (x₀; x_n) сплайн имел как линейно одну непрерывную производную: 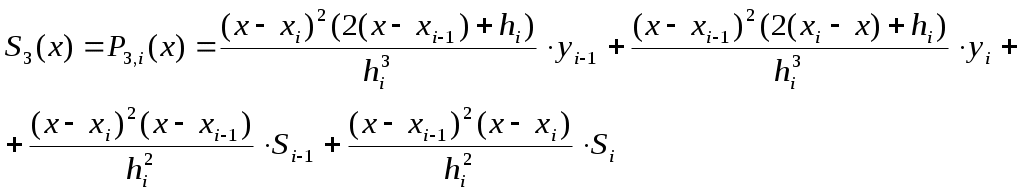Величина называется наклоном сплайна. Т.о., на всём отрезке (x_i-1; x_i) кубический сплайн однозначно определяется величинами

(1)

Фактически задача сводится к определению наклонов сплайна S_i-1 и S_i :

Если в т. x_i , где , нам известны не только величины , но и величины , то естественно предположить: . Получаемый в этом случае сплайн называется естественным.

Можно потребовать, чтобы кубический сплайн имел непрерывную на отрезке от x₀ до x_n 2-ю производную. Для этого наклоны Si д.б. подобраны т.о., чтобы в т.т. стыка x_i у соседних полиномов P_3,i(x) и P_3,i+1(x) совпадали значения 2-х производных: . Используя ф-лу (1), найдём выражения 2-х производных для полиномов на i-ом и i+1-ом участках.





Приравниваем значения 2-х производных в т. стыка, получим систему из n-1 ур. для n+1 неизвестного:



Полученная система явл. не доопределённой.

Если известны численные значения , то найденная система

дополнилась бы 2-я ур.: для левой границы: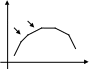








Если численные значения неизвестны, то полученную систему можно привести к системе, определяющий естественный кубический сплайн. В этом случае искусственно полагают вторые производные на границах отрезка x₀ и x_n = 0.

ВОПРОС №14. Многочлен Ньютона с оконченными разностями для интерполяции. Характер экспериментальных данных. Понятие аппроксимации. Метод выбранных точек и средних.

Многочлен Ньютона с конечными разностями для интерполяции. В рассмотренных выше методах не делалось никаких предположений о законе распределения узлов интерполяции. Рассмотрим случай равноотстоящих узлов интерполяции, то есть x_i - x_i-1 = const = h, i=2n. h - называется шагом.

Введем понятие конечных разностей. Пусть известны значения функции в узлах x_i : y_i = f(x_i ). Составим разности значений функции: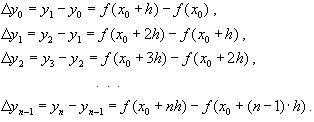



Эти разности называются разностями первого порядка.

Можно составить разности второго порядка:



Аналогично составляются разности k-го порядка:



Выразим конечные разности непосредственно через значение функции: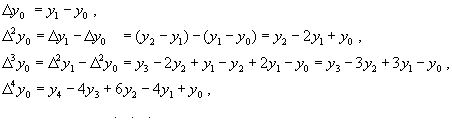



Таким образом, для любого k можно записать:



Запишем эту формулу для значений разности в узле x_i:



Используя конечные разности можно определить



Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в виде:



График многочлена должен проходить через заданные узлы, то есть N(x_i) = y_i(i = 0,n). Используем эти условия для нахождения коэффициентов многочлена: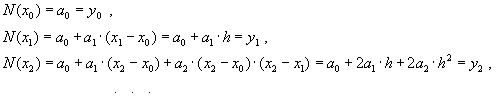



Найдем отсюда коэффициенты a_i :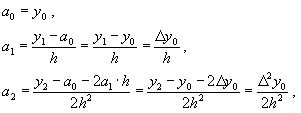



Таким образом для любого k-го коэффициента формула примет вид:



Подставляя эти формулы в выражение многочлена Ньютона получим его следующий вид:



Конечные разности рассчитываются по приведенным выше формулам.

Полученную формулу можно записать в другом виде. Для этого введем переменную



В этом случае: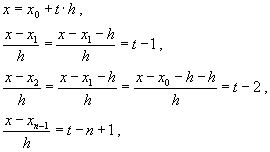



С учетом этих соотношений формулу многочлена Ньютона можно записать в виде:



Полученное выражение может аппроксимировать данную функцию y = f(x) на всем отрезке изменения аргумента [x₀, x_n]. Однако, более целесообразно (с точки зрения повышения точности расчетов и уменьшения числа слагаемых в полученной формуле) ограничиться случаем t < 1, то есть использовать эту формулу для x₀, x, x₁. Для других случаев вместо x₀ принять x_i, если x_i x x_i+1 при i = 0,n-1.

М 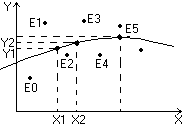етод выбранных точек и средних. Он состоит в следующем: по заданным табл. данным X₀Y наносится система т.

После этого проверяется линия, соответствующая внешнему виду (x) и наиболее близко проходящая от заданных точек:


На проведённой линии выбираются нов. т., не принадлежащие системе табличных данных, а их число д.б = кол-ву не известных параметров эмпирической зависемоти. Значение координат в этих точках тщательно измеряются. Они используются для записи системы уравнений , исходя из условия прохождения графика (x) через эти точки. Решая полученную систему ур., находим неизвестные параметры . Другим методом явл. метод средних. Он базируется на предположении, что параметры функции (x) можно определить из равенства 0 суммы погрешности _i во всех точках X_i:

Из полученного ур. можно вычислить не известные параметры Однако, однозначно рассчитать все m+1 параметр из одного ур. нельзя. Поэтому полученные равенства путём группировки погрешностей _I разделяют на систему m-1 ур-я. Решая полученную систему, находим неизвестные параметры.
ВОПРОС №15. Метод наименьших квадратов.

Для определения параметров эмпирической ф-лы а₀,а₁,…,а_м запишем сумму квадратов отклонений x_i, i=0, n:



Параметры a₀,a₁,...,a_m будем искать при условии минимума функции S = S(a₀,a₁,...,a_m).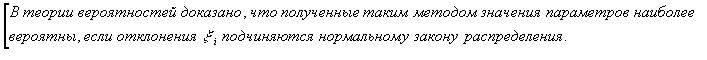



Поскольку в этом случае параметры a₀,a₁,...,a_m выступают в роли независимых переменных функции S (1), то ее min найдем, приравнивая к 0 частные производные по этим переменным: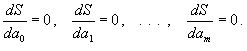



Полученные соотношения представляют собой систему уравнений для определения a₀,a₁,...,a_m.

На практике широко распространен случай, когда в качестве ЭФ используется полином:



Рассмотрим применение МНК для этого случая. Построим сумму квадратов для отклонений:



Найдем частные производные функции S = S(a₀,a₁,...,a_m).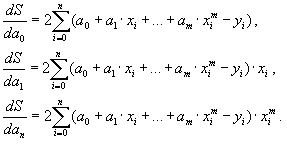



Приравнивая к 0 эти выражения и собирая коэффициенты при неизвестных a₀,a₁,...,a_m, получаем систему уравнений:



Решая полученную СЛАУ получим коэффициенты a₀,a₁,..., a_n многочлена S = S(a₀,a₁,a₁,...,a_n), которые являются исходными параметрами эмпирической формулы.