Шпоры по ВМ. Вопрос 10. Вопросы приближения функций. Постановка задачи. Многочлен Ньютона с распределяющими разностями. 8

• Название: Вопрос 10. Вопросы приближения функций. Постановка задачи. Многочлен Ньютона с распределяющими разностями. 8
• Дата: 19.12.2021
• Размер: 1.12 Mb.
• Имя файла: Шпоры по ВМ.doc
• Тип: Решение; #309079
• страница: 3 из 3

ВОПРОС №17. Численное интегрирование и дифференцирование.

Численное интегрирование.

В 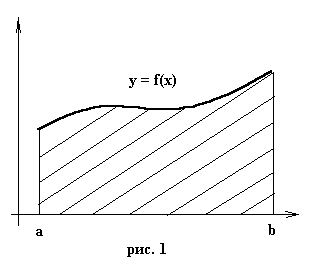прикладных исследованиях часто возникает необходимость вычисления значения определенного интеграла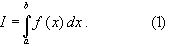



Он может выражать площадь, объем, работу переменной силы и т.д.

Если функция f(x) непрерывна на отрезке [a;b] и ее можно выразить через известные функции, то для вычисления интеграла (1) можно воспользоваться формулой Ньютона- Лейбница: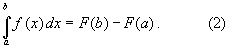



Однако в действительности очень часто получить решение (1) с помощью формулы (2) или других аналитических методов невозможно.

Примером может служить широко применяемый для исследования процессов теплообмена и диффузии, в статистической физике и теории вероятностей интеграл: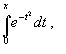



значение, которого не может быть выражено в виде конечной комбинации элементарных функций.

Помимо этого вычисления интеграла (1) в аналитической форме могут быть длительным и трудоемким процессом, приводящим к приближенному результату, или не дающими такового совсем.

На практике помимо аналитических методов широко применяются специальные численные методы. Наиболее широко применяются квадратурные формулы вида: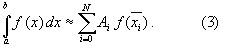



- некоторые т., ∊[a; b] – узлы квадратной ф-лы;

А_i – числовые коэф., называемые весами квадратной формулы.

Выведем простейшие квадратурные формулы, исходя из геометрических соображений. Известно, что интеграл (1) - площадь криволинейной трапеции, ограниченная сверху функцией f(x) (рис.1).

Разобьем отрезок [a;b] на элементарные отрезки [x_i-1,x_i ] точками

При этом интеграл будет представлять сумму своих составляющих.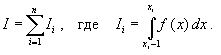



Будем считать шаг h = x_i - x _i-1 постоянным и введем обозначения f_i = f (x_i), f_i-1/2 = f (x_i-1/2),

где x_i-1/2 = (x_i-1/2 + x_i) / 2 - середина элементарного отрезка.


Численное дифференцирование.

Во многих задачах решение включает необходимость вычисления производных. Если функциональная зависимость f(x) имеет простой вид, то в вычислительных алгоритмах можно использовать явный вид производной f `(x) для определения ее числовых значений. Однако, в реальных ситуациях, функция f(x) может быть представлена математической моделью или конечным множеством точек (x_i; f_i(x)). В этом случае отсутствует возможность пользоваться аналитическим выражением производной.

Вспомним определение производной:

можно использовать приближенное числовое значение:

- пр-я слева - слева

Вторую производную в точке x_i можно рассчитать по этой же формуле:



и так далее.

Данные формулы дают достаточно высокую точность при задании h→0

Выходом в данной ситуации может быть использование алгоритмов интерполяции.
ВОПРОС №18. Общая постановка задачи Коши. Метод Эйлера для её решения.

Численное решение задачи Коши. При рассмотрении технических систем и технологических процессов инженеру часто приходится сталкиваться с их характеристиками, которые непрерывным образом меняются во времени t. Такие явления подчиняются физическим законам, описываемым дифференциальными уравнениями. Одной из основных математических задач, решаемых для таких уравнений, является задача Коши. Обычно, к ней приходят, когда известно начальное состояние системы в момент времени t₀ и требуется предсказать ее поведение в момент времени t > t₀.

Рассмотрим задачу Коши для дифференциального уравнения первого порядка: 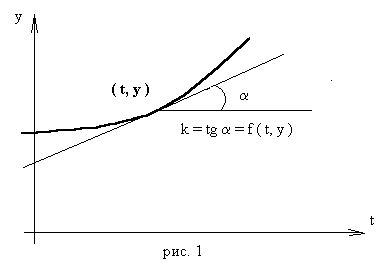(1)

Решением уравнения (1) является дифференцируемая функция y(t), которая при подстановке в уравнение (1) превращается в тождество. График y(t)

называется интегральной кривой рис. (1), а процесс решения называется интегрированием.

Заметим, что уравнение (1) задает в каждой точке (t, y) тангенс угла наклона касательной к графику решения, проходящего через эту точку.

Если в каждой точке (t, y) задать с помощью некоторого вектора направление касательной, определенной значением f (t, y), то получится поле направлений.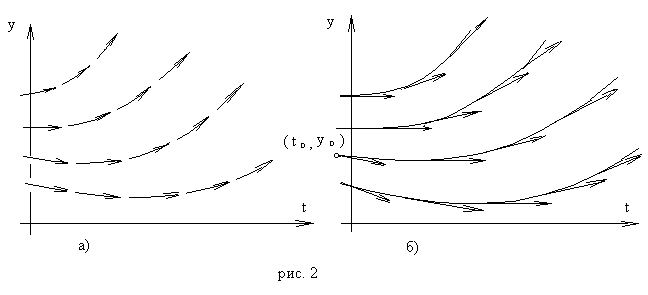


Геометрическая задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной. Для того чтобы выделить из семейства решений дифференциального уравнения (1) конкретное решение, задают начальное условие: y(t₀)=y₀

Метод Эйлера решения задачи Коши. Воспользуемся формулой Тейлора:

(2)

R_(p+1)(t,h) - остаточный член. Если его отбросить, то получим приближенное равенство:



Если значение решения у в т. t известно, то в силу равенства (1) можно считать известными y’(t). Для нахождения производных 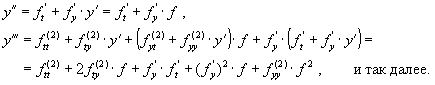продифференцируем Ур. (1) по t. Получим:

Выражения усложняются по мере роста порядка K.

Использование приближенной формулы (3) приводит к формуле: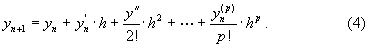



Метод Эйлера является первым и простейшим методом решения задачи Коши. Его можно получить, если в приближенном равенстве (4) положить p = 1, то есть оставить два первых слагаемых. Получим:

Геометрическая интерпретация одного шага метода Эйлера заключается в аппроксимации решения на отрезке [tn, tn+1] касательной y = yn + y' (tn) (t-tn), проведенной в точке (tn,yn) к интегральной кривой, проходящей через эту точку. Таким образом, после выполнения N шагов неизвестная интегральная кривая заменяется ломаной линией, для которой угловой коэффициент k_n очередного n - го звена равен значению f (t_n, y_n). (рис. 3)

Погрешность аппроксимации в этом случае имеет вид:
ВОПРОС №19. Общая постановка задачи Коши. Метод Рунге – Кутта для её решения. Метод Рунге – Кутта 4-го порядка точности.

Численное решение задачи Коши. (ВОПРОС №18)

Метод Рунге - Кутта решения задачи Коши. Является наиболее популярным из одношаговых методов. Пусть y (t) - решение дифференциального уравнения y' = f (t,y), удовлетворяющее условию y (t_n) = y_n. Из формулы Ньютона - Лейбница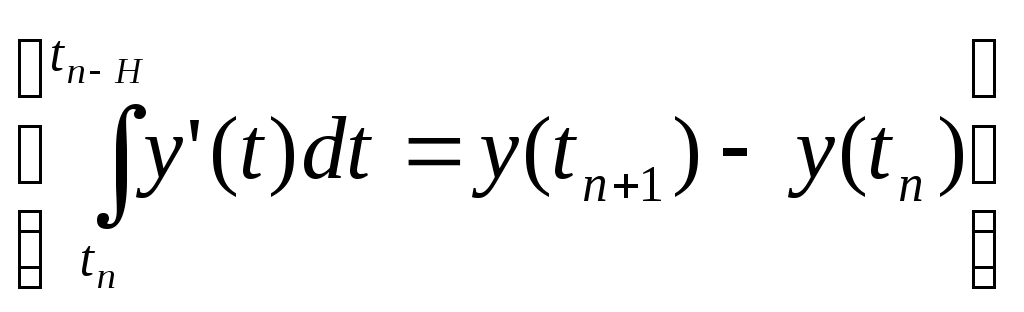



следует: 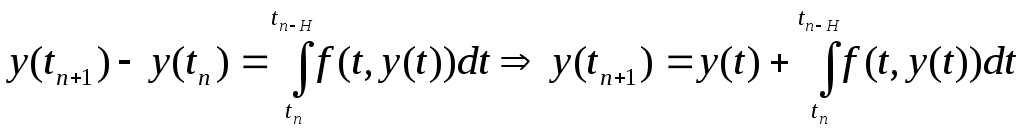(6)

Если интеграл в формуле (6) можно было вычислить точно, то получилось бы простое выражение. Однако, в действительности это невозможно, поэтому будем строить приближенную формулу, заменив интеграл квадратурной суммой. Введем на отрезке [t_n,t_n+1] m вспомогательных узлов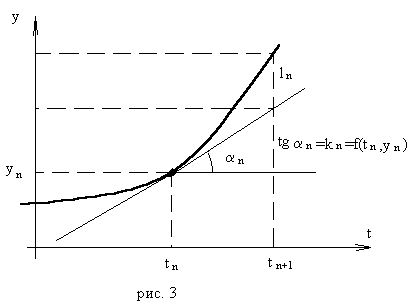

где

Заменяя, входящий в равенство (6) интеграл квадратурной суммой с узлами t_n⁽¹⁾, ... ,t_n^(m), получим приближенное равенство: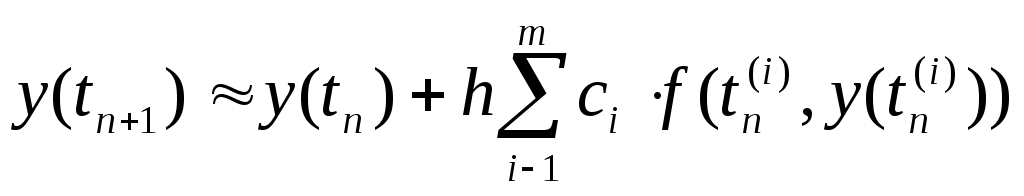

(7)

Однако воспользоваться равенством (7) нельзя, т.к. значения y в т. 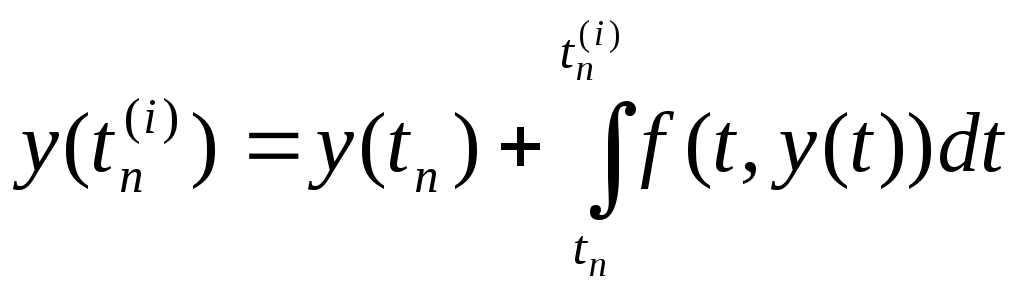неизвестны. Чтобы найти их запишем:

(8)

Заменяя в этом равенстве для каждого i входящий в него интеграл соответствующей квадратурной формулой с узлами t_n⁽¹⁾, t_n ⁽²⁾, ... , t_n^(i-1), получим приближенные равенства: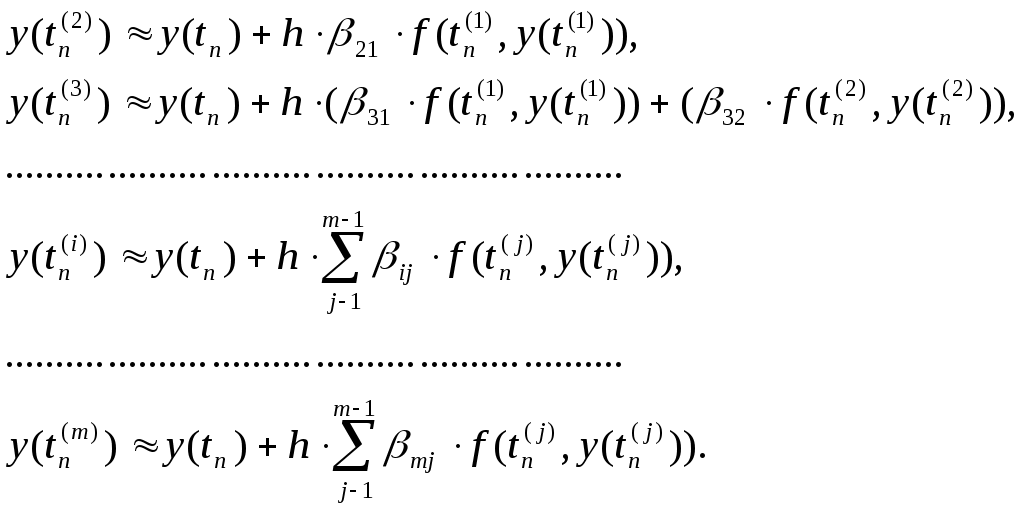



позволяющие последовательно вычислить приближения k y(t_n⁽²⁾), ..., y(t_n^(m)). Обозначим через y_n⁽ⁱ⁾ вспомогательные величины, являющиеся приближениями k y(t_n⁽ⁱ⁾). Пусть k_n⁽ⁱ⁾ = f (t_n⁽ⁱ⁾, y_n⁽ⁱ⁾) - приближение к значению углового коэффициента k в точке t_n⁽ⁱ⁾. В этом случае расчетные формулы примут вид: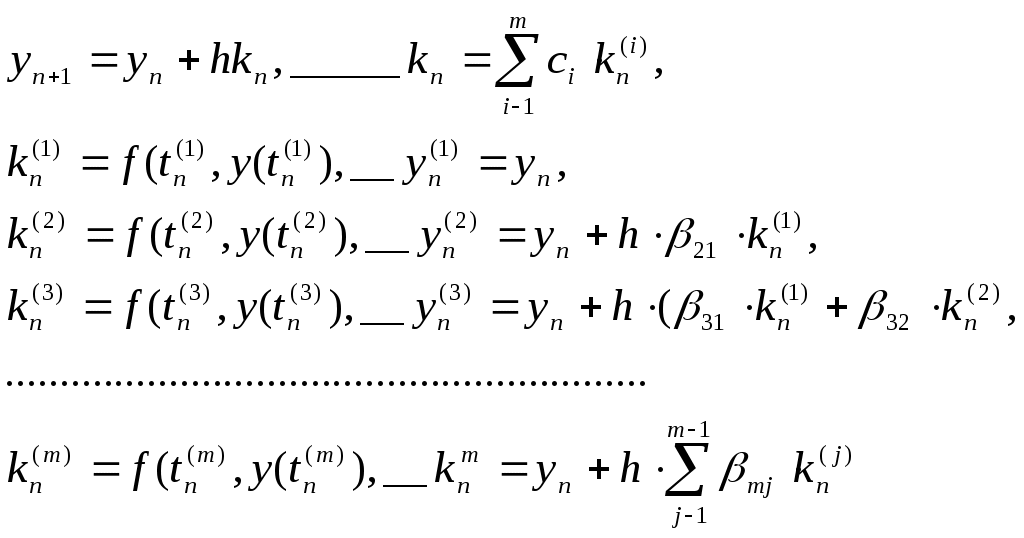



Если выбросить вспомогательные величины y_n⁽ⁱ⁾, то те же формулы можно записать в виде: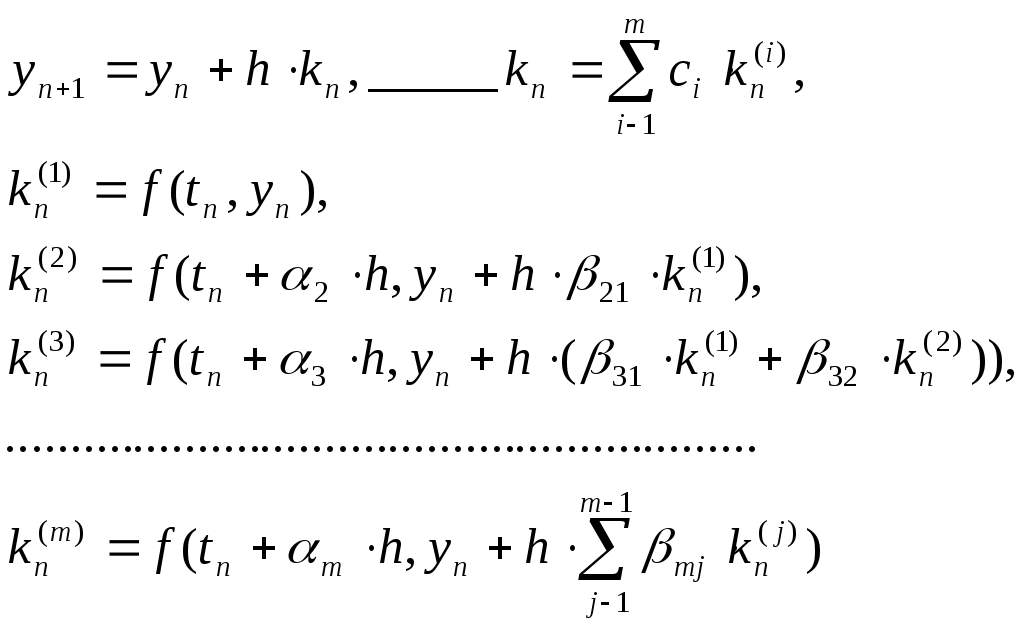



Полученный метод носит название m - этапного метода Рунге - Кутта.

Выбор конкретных значений параметров осущ. исходя из различных соображений, одним из кот. м. б. желание сделать порядок аппроксимации максимально возможным.

Метод Рунге - Кутта четвертого порядка точности: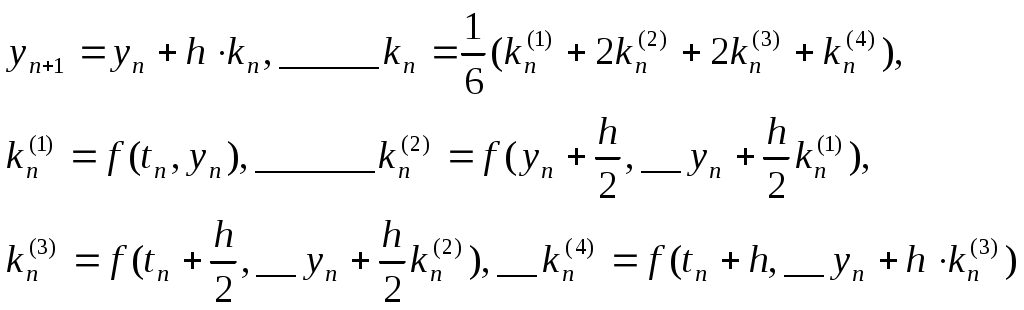

ВОПРОС 20. Постановка 2-х точной краевой задачи. Её

ДКЗ представляет собой задачу отыскивания реш. обыкновенного диф. ур. на отр. [а; б] при условии, что реш. заданы на обоих краях отрезка. Рассмотрим методы реш. задач этого класса, кот. можно записать в виде: U''(x)=f(x, u); на примере стационарного ур. теплопроводности:

. Здесь k(x) играет роль коэф. теплопроводности, - плотность потока тепла. Помимо этого, указанное ур. может описать процесс диффузии газов, деформированию ступ и ступеней, распределение эл. магнитных волн, установившееся распределение плотности патронов в реакторе и многое другое.

Предпримем, что ф-и q(x), k(x), f(x) известны и выполняется условие k(x)>0, q(x)>0. Тогда распределение температуры в стержне, описывание ф-ей f(x), м.б однозначно определено при задании состояния U(x) на границах отрезка [a, b], т.е U(a)=Ua, U(b)=Ub. Такие краевые условия наз. краевыми условиями 1-го рода. Часто краевую задачу записывают в операторном виде: 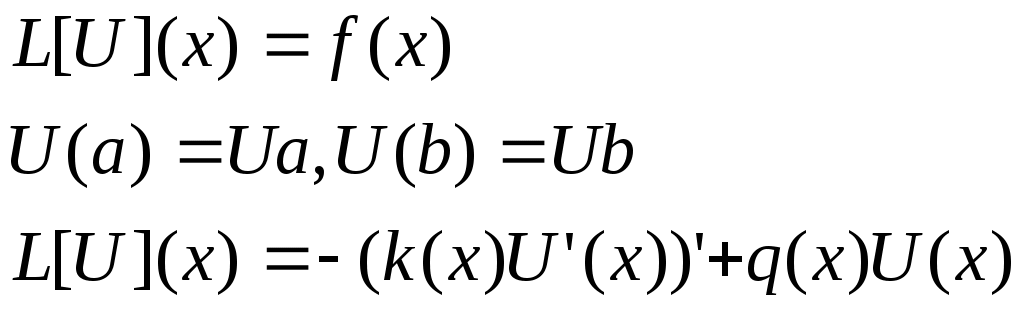L[U](x) – диф. оператор

Одним из широко распространенных методов реш. задачи (1) с ограничением (2) явл. метод конечных разностей. В этом методе область непрерывного аргумента заменяет конечным множеством точек (сеткой). После этого вместо ф-ии непрерывного арг. рассмотренные вводится ф-ия, определяющаяся только в узлах сетки (сеточная ф-ия). В этом случае произвед. м. б заменены своими разностными аналогами, т. е приближенно численными выражениями. В итоге исходная краевая задача заменяется дискретной краевой задачей или разностной схемой, представляющей собой сист. линейных и нелинейных алгебраич. ур., реш. кот. приблизительно принимает за реш. исходной задачи.

Зададим k(x)=1. В этом сл-е исх. задача примет вид. -U''(x)+q(x)U(x)=f(x) (3)

U(a)=Ua, U(b)=Ub (4)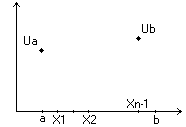

Заменим отрезок [a; b] непрерывного арг. Х сеткой, кот. обозначим . где х₀=а, х_n=b

∂^h – граница отрезка.

В результате реш. задачи 3 после подмены непрерывной ф-ии U(x) сеточной ф-ей будет найдена сеточная ф-я U^h, такая, что

В результате диф. ур. (3) заменяется следующим:

Будем считать, что ф-ия U^h во всех узлах сетки W^h удовлетворяет ур. (5). В этом случае ур. (5) явл. разностным ур. аппроксимации краевой задачи (1) с ограничением (2), фактически явл. системой линейной алгебры уравнений. Преобразуем ур. (5): -U_i-1 +U_i(2+h²q_i)-U_i+1=h²f_i.

U₀=U_a

U_n=U_b

Полученную систему удобно реш. методом прогонки. М-д прогонки предназначен для реш. трёх диагональных матриц: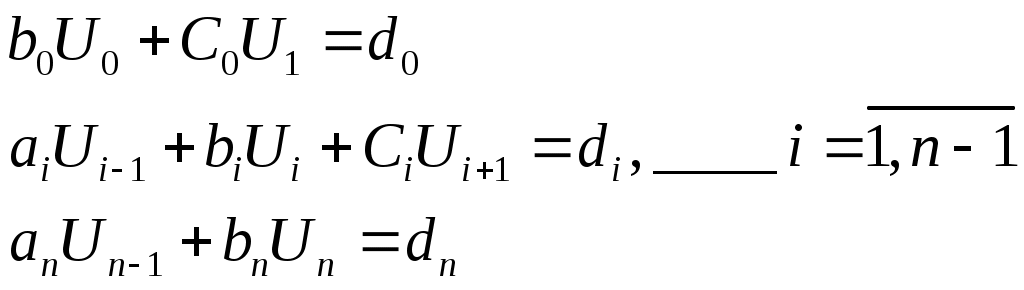

Прямой ход заключается в расчёте прогоночных коэф. α и β. На обратном ходе выч. знач. неизвестной ф-ии.







Значения ф-ии U_i выч. на обратном ходе: U_n=β_n U_i=α_iU_i+1+β_i,

ВОПРОС №21. Вычисление собственных чисел матрицы.

В процессе конструирования и анализа больших технич. систем инженеру очень часто приходится сталкиваться с задачей нахожд. собств. чисел и собственных векторов исследуемой системы, кот. характеризуют её внутренние св-ва. Математически задача нахождения собственного числа выглядит след. образом: Пусть задана квадратная матрица Аm,m. Обозначаем скалярное произведение 2-х векторов: - норма.

Число  явл. собств. числом матрицы А, если найдётся ненулевой вектор Х, для кот. вып. равенство

(1) Ах = х. В этом случае вектор Х наз. собственным вектором матрицы А. Запишем (1) в др. виде:

(А-Е)х=0 (2). Е – единичная матрица. Эта система будет им. ненулевое решение тогда, когда определитель матрицы det (A-E)=0 (3). Раскрывая ур. (3), мы получаем характеристическое ур. вида: 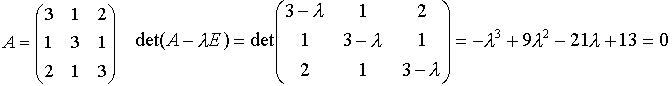. Известно, что алгебраическое ур. степени m им. m корней в области комплексных чисел, т.е люб. матрица А порядка m им. ровно m собственных значений, комплексно сопряжённые. Во многих дисциплинах сущ. задачи, связывающие с выч. всех собств. чисел. В этом случае задача наз. полной проблемой собственных значений. Однако, гораздо чаще в задачах треб. определить одно собственное значение или некоторую их часть. Такие задачи наз. частичной проблемой собственных значений. В плане постановки такой задачи существующий интерес представляет нахождение собственного числа, наиболее близкого расположенного к заданному, или нахождение наибольшего или наименьшего собственного числа. Характеристическое ур. можно решать любым численным методом с последующим понимание порядка ур. после нахождения одного из корней. Пример:



₁=1; делим на -1: -²+8-13=0 → ₂=4±

Описанный приём для реш. характерного ур. относят к прямым методам реш. проблем собственных значений. Их применению может воспрепятствовать высокий порядок m, когда корни характеристического ур. становятся чувствительны к погрешности и м.б потеряна достоверная инф. об m величене. Рассмотрим один из самых простых методов реш. задачи о собственных числах – степенной метод без сдвигов. Пусть требуется определить max по модулю собственное значение ₁ матрицы А. ₁ д.б вещественным. Возмём произвольный вектор х⁰ и построим из него последовательность векторов и Итерационный процесс:

Теорема: Пусть задана матрица А достаточно простой структуры, для кот. |₁|>|₂|≥|₃|≥…≥|_m|. Предположим что разложение х⁽⁰⁾ по базису собственных векторов х⁰=С₁е₁+ С₂е₂+…+ С_mе_m происходит с С₁≠0. Тогда |^k₁| → |₁|^k→∞и справедлива следующая оценка погрешности:

Исходя из формулы (4), можно записать, что х^(к)=А^к х⁽⁰⁾. Допускается следующее усовершенствование метода: y^(к)=Ах^(k-1), ^(к)=( y^(к), y^(к-1)), Для того. чтобы схема была работоспособной, нужно, чтобы ||x⁽⁰⁾||=1. Подобный подход позволяет избежать возникших в результате вычислений проблем с переполнением или потерей порядка. Одним из недостатков степенного метода без сдвигов явл. его медленная сходимость применительно ко многим прикладным задачам.