рооо. Курсовая работа Комплексные числа. 2. Решение задач 17
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
СодержаниеВведение 2 1.Комплексные числа 5 1.1. Основные определения и действия с комплексными числами 5 1.2. Геометрическая интерпретация комплексного числа 10 1.3. Тригонометрическая форма комплексных чисел 12 2.Решение задач 17 2.1. Действия с комплексными числами в алгебраической форме 17 2.2. Геометрическое представление комплексных чисел 21 2.3. Действия с комплексными числами в тригонометрической форме 27 Список используемой литературы 35 ВведениеЧисла – один из основных математических объектов. Понятие числа является основным стержнем всего школьного курса математики, пронизывающим этот курс от первого до последнего класса. Сначала для умения считать учащиеся знакомятся с натуральными числами. Для того чтобы сделать возможным деление одного числа на другое, вводятся дробные числа, для возможности вычитания из меньшего числа большего вводятся отрицательные числа, для того чтобы иметь возможность описать результат измерения длины в случае, когда отрезок несоизмерим с выбранной единицей длины, вводится иррациональное число. Присоединение каждого последующего класса чисел к предыдущему расширяет сферу применений этого понятия. Учащиеся твердо усвоили, что квадратный корень из отрицательного числа среди действительных чисел не существует. Однако потребности самой алгебры и ее приложений требуют такого расширения понятия числа, при котором действие извлечение квадратного корня из отрицательного числа стало бы осуществимым. Если ввести понятие множества комплексных чисел, то квадратное уравнение всегда будет иметь корни. И, конечно, только в старших классах уместен достаточно полный, систематизирующий ретроспективный взгляд на общую картину завершившегося эволюционного процесса. Впервые настоятельная необходимость рассмотрения комплексных чисел встретилась в XVI веке, когда несколько итальянских математиков открыли возможность алгебраического решения уравнений 3-й степени. При переходе в область комплексных чисел многие предположения алгебры становятся более простыми и симметричными. Так, квадратное уравнение с действительными или комплексными коэффициентами всегда имеет два корня, различных или совпадающих. Корень n-й степени из отличного от нуля действительного или комплексного числа всегда имеет n различных значений и т.д. Вместе c тем теоретическое и прикладное значение комплексных чисел выходит далеко за пределы алгебры. Сильно продвинутая в течение XIX столетия теория функций комплексной переменной оказалась исключительно ценным аппаратом для исследования почти всех разделов теоретической физики, таких как теория колебаний, гидродинамика, теория элементарных частиц и т.д. Цель спроса работы товаров в изложении теоретических основ и применении их при решении задач с комплексными числами, которые встречаются в углубленном курсе алгебры и начал математического анализа. Объектом производитель является тема комплексные числа, изучаемая в углубленном курсе алгебры и начал математического анализа. Предметом исследования являются задачи, встречающиеся в 10-11 классах, при изучении темы «Комплексные числа». В соответствии с поставленной целью, необходимо решить следующие задачи: 1. Изучить основы теории, а именно рассмотреть алгебраическую, геометрическую и тригонометрическую форму комплексных чисел. 2. Рассмотреть комплекс задач на применение основных действий с комплексными числами в алгебраической форме. 3. Рассмотреть комплекс задач, связанных с геометрической иллюстрацией комплексных чисел. 4. Рассмотреть комплекс задач, связанных с представлением в тригонометрической форме, а также извлечение корня, возведение в степень комплексных чисел. Комплексные числа1.1. Основные определения и действия с комплексными числамиКомплексным числом называют выражение вида 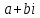 , где , где 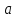 и и 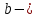 действительные числа, а действительные числа, а 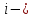 формальный символ (буква), для которого по определению выполняется равенство формальный символ (буква), для которого по определению выполняется равенство 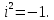 [] []Слово «комплексные» происходить от слова «составные» - по виду выражения 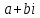 . Действительные числа . Действительные числа 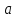 и и 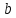 , из которых составляется комплексное число , из которых составляется комплексное число 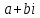 , называются компонентами этого числа. Число , называются компонентами этого числа. Число 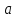 называется действительной частью комплексного числа называется действительной частью комплексного числа 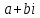 , вторая компонента , вторая компонента 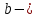 его мнимой частью. Число его мнимой частью. Число 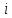 называют мнимой единицей. называют мнимой единицей.Например, действительная часть комплексного числа 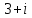 равна 3, мнимая часть равна 1. Запись комплексного числа в виде равна 3, мнимая часть равна 1. Запись комплексного числа в виде 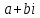 называют алгебраической формой комплексного числа. называют алгебраической формой комплексного числа.Два комплексных числа 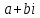 и и 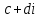 называются равными в том и только том случае, когда называются равными в том и только том случае, когда 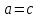 и и 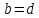 , т. е. когда равны их действительные и мнимые части. , т. е. когда равны их действительные и мнимые части.Например, 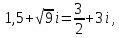 так как так как 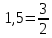 , , 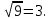 Сложение и умножение комплексных чисел. Операции сложения и умножения двух комплексных чисел определяются следующим образом. Сложение комплексных чисел 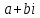 и и 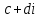 определяется правилом определяется правилом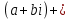 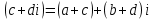 . (1.1.1) . (1.1.1)Умножение комплексных чисел 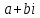 и и 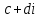 определяется правилом определяется правилом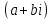 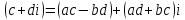 . (1.1.2) . (1.1.2)Формула (1.1.1) означает, что сложение производится по обычному правилу сложения многочленов с произведением подобных членов. Формула (1.1.2) означает, что умножение комплексных чисел осуществляется по обычному правилу умножения многочленов, только, считая, что 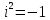 . .Принято считать, что 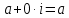 , т.е. комплексное число , т.е. комплексное число 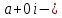 это действительное число это действительное число 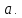 Число вида 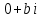 обозначают обозначают 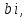 т.е. т.е. 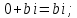 его называют чисто мнимым числом. его называют чисто мнимым числом.Комплексное число 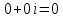 является единственным числом, которое одновременно и действительное, и чисто мнимое. является единственным числом, которое одновременно и действительное, и чисто мнимое.Комплексное число принято обозначать одной буквой, чаще всего буквой z. Запись 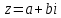 обозначает, что комплексное число обозначает, что комплексное число 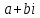 обозначается буквой обозначается буквой 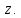 Операции сложения и умножения комплексных чисел обладают такими же свойствами, как и операции для действительных чисел. Основные свойства сложения и умножения комплексных чисел Переместительное свойство 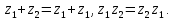 Сочетательное свойство 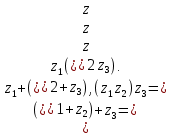 Распределительное свойство 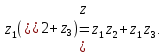 Сложения, умножение комплексных чисел фактически связаны с действительными числами-компонентами комплексного числа. Их можно изложить не используя символ 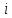 . Для этого достаточно писать вместо . Для этого достаточно писать вместо 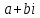 пару действительных чисел пару действительных чисел 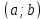 . .Комплексным числом zназывают пару 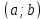 действительных чисел действительных чисел 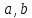 , взятых в определенном порядке. , взятых в определенном порядке.Тогда изложенные выше правила будут выглядеть следующим образом: 1. 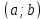 = =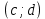 в том и только том случае, если в том и только том случае, если 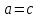 и и 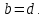 2. 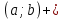 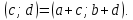 3. 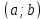 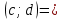 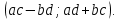 4. 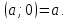 Число 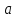 называют действительной частью комплексного числа и обозначают называют действительной частью комплексного числа и обозначают 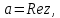 число число 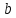 называют мнимой частью комплексного числа и обозначают называют мнимой частью комплексного числа и обозначают 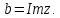 Комплексные числа 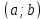 при при 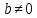 называют мнимыми числами, а числа вида называют мнимыми числами, а числа вида 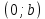 называют чисто мнимыми числами. называют чисто мнимыми числами.Комплексные числа 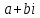 и и 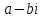 , отличающиеся знаком мнимой части, называются сопряженными. Если , отличающиеся знаком мнимой части, называются сопряженными. Если 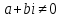 , то , то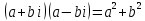 есть положительное действительное число. Обозначается сопряженное число 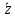 , т.е. , т.е.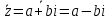 . .Например, 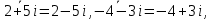 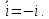 Отметим, что 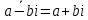 , поэтому для любого комплексного числа , поэтому для любого комплексного числа 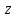 имеет место равенство имеет место равенство 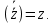 Равенство 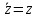 справедливо тогда и только тогда, когда справедливо тогда и только тогда, когда 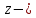 действительное число. действительное число.Модулем комплексного числа 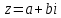 называется число называется число 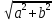 , т.е. , т.е.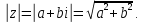 (1.1.3) (1.1.3)Например, 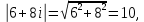 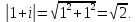 Из формулы (1.1.3) следует, что 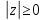 для любого комплексного числа для любого комплексного числа 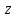 , причем , причем 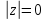 тогда и только тогда, когда тогда и только тогда, когда 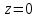 , т.е. когда , т.е. когда 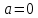 и и 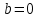 . .Для любого комплексного числа 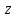 справедливы формулы справедливы формулы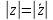 , , 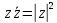 . .Вычитание комплексных чисел. Комплексное число 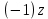 называется противоположным комплексному числу называется противоположным комплексному числу 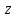 и обозначается и обозначается 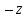 . .Если 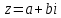 , то , то 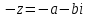 . Например, . Например, 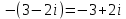 . .Для любого комплексного числа 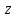 выполняется равенство выполняется равенство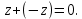 Вычитание комплексных чисел вводится как операция, обратная сложению: для любых комплексных чисел 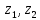 существует, и притом только одно, число существует, и притом только одно, число 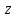 , такое что , такое что 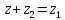 (1.1.4) (1.1.4)т.е. уравнение (1.1.4) имеет только один корень. Прибавим к обеим частям равенства (1.1.4) число 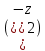 , противоположное числу , противоположное числу 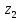 : :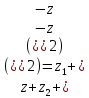 , откуда , откуда 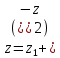 . .Число 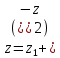 обычно обозначают обычно обозначают 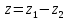 и называют разностью чисел и называют разностью чисел 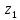 и и 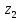 . .Если 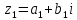 , , 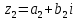 , то разность , то разность 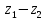 имеет следующий вид: имеет следующий вид: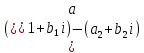 = =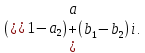 (1.1.5) (1.1.5)Формула (1.1.5) показывает. Что разность комплексных чисел можно находить по правилам действий с многочленами. Деление комплексных чисел. Деление комплексных чисел вводится как операция, обратная умножению: для любых комплексных чисел 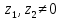 существует, и притом только одно, число существует, и притом только одно, число 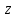 , такое, что , такое, что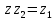 т.е. это уравнение относительно z имеет только один корень, который называется частным чисел т.е. это уравнение относительно z имеет только один корень, который называется частным чисел 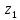 и и 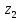 и обозначается и обозначается 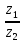 , или , или 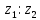 т.е. z= т.е. z=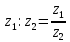 . .Комплексное число нельзя делить на нуль. Итак, частное комплексных чисел 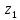 и и 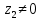 можно найти по формуле можно найти по формуле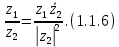 Каждое комплексное число z, не равное нулю, имеет обратное ему число w, такое, что z 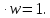 Если Если 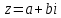 , ,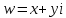 , то это равенство принимает вид , то это равенство принимает вид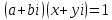 или или 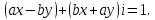 Из последнего равенства получаем систему 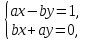 решая которую находим 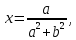 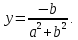 Таким образом, если 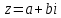 , то число, ему обратное, принимает вид , то число, ему обратное, принимает вид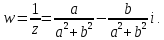 Если 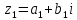 , , 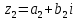 , то по формуле (1.1.6) можно представить в виде , то по формуле (1.1.6) можно представить в виде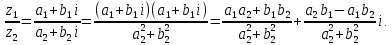 Вместо того чтобы запоминать эту формулу, следует запомнить, что результат для частного получается посредством умножения числителя и знаменателя на число сопряженное со знаменателем. Например, 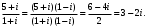 |
