рооо. Курсовая работа Комплексные числа. 2. Решение задач 17
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
1.3. Тригонометрическая форма комплексных чиселПусть вектор 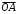 задается на комплексной плоскости числом задается на комплексной плоскости числом 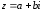 Обозначим через φ угол между положительной полуосью Ox и вектором Обозначим через φ угол между положительной полуосью Ox и вектором 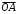 (угол φ считается положительным, если он отсчитывается против часовой стрелки, и отрицательным в противном случае). (угол φ считается положительным, если он отсчитывается против часовой стрелки, и отрицательным в противном случае). 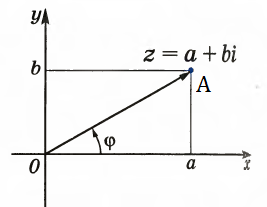 Рис. 1.3.1 Обозначим длину вектора 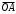 через r. Тогда через r. Тогда 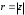 , а , а 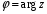 (величина угла, образованного направлением радиуса вектора, изображающего число z, с действительной осью называется аргументом числа z). Модуль и аргумент комплексного числа (величина угла, образованного направлением радиуса вектора, изображающего число z, с действительной осью называется аргументом числа z). Модуль и аргумент комплексного числа 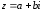 связаны с его компонентами при помощи формул связаны с его компонентами при помощи формул . .Эти формулы непосредственно следуют из определения функций cos и sin любого угла. Ясно, что 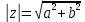 , , 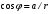 , , 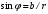 . Эти формулы определяют модуль и аргумент по данным a и b. Для определения аргумента можно пользоваться формулой . Эти формулы определяют модуль и аргумент по данным a и b. Для определения аргумента можно пользоваться формулой 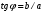 при при 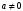 . Однако эта формула задает . Однако эта формула задает 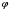 лишь с точностью до кратности лишь с точностью до кратности 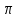 (т.е. полуоборота), а не до кратного (т.е. полуоборота), а не до кратного 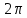 . Это заставляет дополнительно выбирать из двух значений . Это заставляет дополнительно выбирать из двух значений 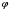 в противоположных четвертях одно, по знаку в противоположных четвертях одно, по знаку 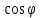 (или (или 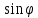 ), совпадающему со знаком a (соответственно b). ), совпадающему со знаком a (соответственно b).Подставляя вместо компонент комплексного числа 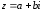 их выражения через модуль и аргумент, получаем их выражения через модуль и аргумент, получаем 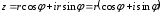 . .Такая форма записи комплексного числа называется тригонометрической. Например, представить число 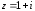 в тригонометрической форме. в тригонометрической форме.В комплексном числе 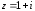 : : 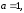 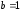 . . Тогда 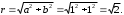 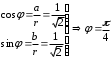 , ,Поэтому 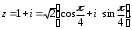 Комплексное число из тригонометрической также можно представить в показательной форме записи: 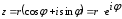 . .Умножение и деление комплексных чисел в тригонометрической форме. Пусть 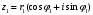 и и 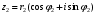 . Тогда . Тогда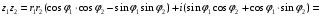 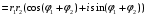 . .Таким образом, 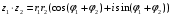 . .Из данной формулы следует, что при перемножении комплексных чисел их модули перемножаются, а аргументы складываются. А теперь вычислим частное этих комплексных чисел ( 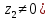 : :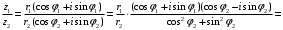 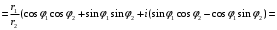 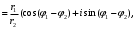 Таким образом, 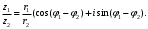 Из полученного равенства следует, что модуль частного двух комплексных чисел равен частному модулей делимого и делителя, а разность аргументов делимого и делителя является аргументов частного. При возведении в натуральную степень комплексного числа справедлива формула 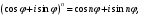 которую называют формулой Муавра. Для возведения в n-ю степень комплексное число, записанное в тригонометрической форме 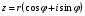 , справедлива формула , справедлива формула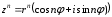 . . При извлечении корня из комплексного числа используется формула: 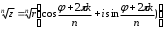 , ,где k=0, 1, 2, …, n-1. где 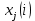 – разница между наибольшими суточными температурами воздуха j-го и (j-1)-го дня в i – й год (года занумерованы последовательно с 1912 года). – разница между наибольшими суточными температурами воздуха j-го и (j-1)-го дня в i – й год (года занумерованы последовательно с 1912 года). Наблюдаемые и расчётные оценки параметров метеорологических процессов являются случайными величинами. Их вероятностное поведение описывается с помощью функции распределения. Распределения метеорологических элементов, не имеющих легко достижимых физических пределов и асимметрия которых не очень велика (температура воздуха и почвы, атмосферное давление и т.п.) в большинстве случаев описываются нормальной функцией распределения [Исаев 1988]. Гипотеза о согласованности выше указанных статистических данных с нормальным распределением по критерию хи-квадрат подтвердилась. Далее с помощью линейного параметрического коэффициента парной корреляции было установлено, что взаимосвязь между элементами этих выборок является очень слабой и позволяет считать значения выборок независимыми. Таким образом, выборки (1) можно считать реализациями 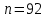 независимых, одинаково распределенных гауссовских случайных величин независимых, одинаково распределенных гауссовских случайных величин 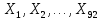 . .Далее была построена выборка из максимумов значений центрированных и нормированных последовательностей (1): 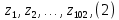 где 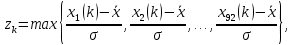 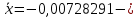 математическое ожидание, математическое ожидание, 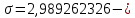 среднее квадратическое отклонение (вычислены по объединенной выборке). При этом максимумы последовательностей (1) (максимумы скачков наибольших суточных температур за летний сезон) среднее квадратическое отклонение (вычислены по объединенной выборке). При этом максимумы последовательностей (1) (максимумы скачков наибольших суточных температур за летний сезон)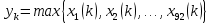 связаны с 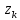 равенством: равенством: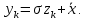 Таким образом, выборочные значения (2) представляют статистические данные для исследования и моделирования поведения случайной величины 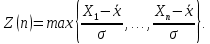 При этом 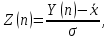 где 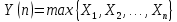 , ,следовательно, имеется равносильность событий 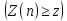 и и 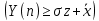 , то есть , то есть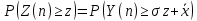 . .Статистическая согласованность выборки (1) с нормальным распределением позволяет для центрированных и нормированных максимумов перепадов температур (2), использовать предельное двойное экспоненциальное распределение: 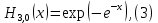 с центрирующей и нормирующей константами, вычисляемыми по следующим формулам 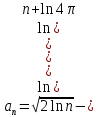 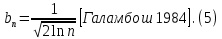 В связи с тем, что предельные теоремы справедливы при условии, что 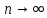 , то точность построенной модели во многом зависит от объема выборок, из которых берутся максимумы. Поскольку в нашем случае , то точность построенной модели во многом зависит от объема выборок, из которых берутся максимумы. Поскольку в нашем случае 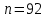 (объемы выборок, из которых выбирались максимумы), то для последовательности (объемы выборок, из которых выбирались максимумы), то для последовательности 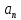 также необходимо учитывать возможность поправки порядка бесконечно малой функции также необходимо учитывать возможность поправки порядка бесконечно малой функции 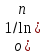 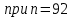 . .Таким образом, по формулам (4), (5) с учетом поправки вычислили значения центрирующей и нормирующей констант: 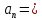 2,114405; 2,114405; 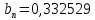 . .Оценка соответствия эмпирического распределения двойному экспоненциальному показала, что во всех случаях отклонения фактических частот можно считать случайными, и при уровне значимости 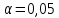 гипотеза о согласованности выборочных данных (2) с двойным экспоненциальным распределением по критерию хи-квадрат подтвердилась. Гистограмма эмпирических частот представлена на Рис. 1. гипотеза о согласованности выборочных данных (2) с двойным экспоненциальным распределением по критерию хи-квадрат подтвердилась. Гистограмма эмпирических частот представлена на Рис. 1. Таким образом, для моделирования поведения максимальных скачков наибольших суточных температур целесообразно использовать двойное экспоненциальное распределение. Построение моделей на его основе позволяет анализировать данные метеонаблюдений с точки зрения поведения наибольших суточных колебаний. Значения наблюдаемых и теоретических частот, вычисленных с помощью двойного экспоненциального распределения приведены в таблице 1. В таблице 2 представлены вероятности и соответствующие им относительные частоты событий 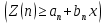 , состоящие в превышении максимом указанных значений. По результатам, представленным в этой таблице, наибольшая разница между относительной частотой и вероятностью указанных событий составляет 0,02. , состоящие в превышении максимом указанных значений. По результатам, представленным в этой таблице, наибольшая разница между относительной частотой и вероятностью указанных событий составляет 0,02.Используя теоретическое распределение (3) величины 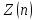 , можно сделать прогноз, что приблизительно в 95% летних сезонов значения максимальных скачков наибольших суточных температур воздуха будут менее 8,69 градусов. За рассмотренный период в 102 года скачок, превышающий это значение, наблюдался 3 раза, что составляет 3% от периода наблюдения . , можно сделать прогноз, что приблизительно в 95% летних сезонов значения максимальных скачков наибольших суточных температур воздуха будут менее 8,69 градусов. За рассмотренный период в 102 года скачок, превышающий это значение, наблюдался 3 раза, что составляет 3% от периода наблюдения .Таким образом, сравнительный анализ полученных теоретических и наблюдаемых частот событий, характеризующих поведение максимальных скачков наибольших суточных температур воздуха в летний сезон в городе Курске за столетний период наглядно иллюстрирует точность построенной модели и подтверждает возможность прогнозирования метеорологических показателей не только в области их усредненных значений, но и в области их экстремумов. |
