рооо. Курсовая работа Комплексные числа. 2. Решение задач 17
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
Решение задач2.1. Действия с комплексными числами в алгебраической формеЗадача 1. Выполните следующие действия над комплексными числами: а) 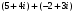 ; б) ; б) 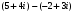 ; в) ; в) 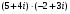 ; г) ; г) 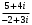 . .Решение: Используя формулы (1.1.1), (1.1.2) …. вычислим а) 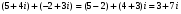 ; ; б) 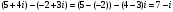 ; ;в) 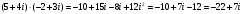 ; ;г) 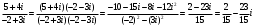 . .Ответ: а) 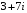 ; б) ; б) 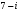 ; в) ; в) 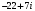 ; г) ; г) 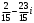 . .Задача 2. Выполните действия с комплексными числами в алгебраической форме: а) 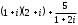 ; б) ; б) 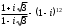 ; в) ; в) 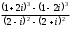 . .Решение: а) 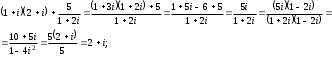 б) 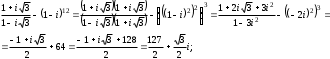 в) 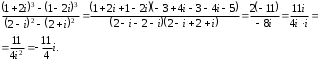 Ответ: а) 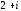 ; б) ; б) 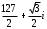 ; в) ; в) 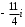 . .Задача 3. Вычислите 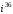 ; ; 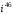 ; ; 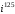 ; ; 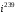 . .Решение: 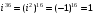 ; ; 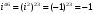 ; ;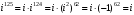 ; ; 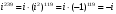 . .Ответ: 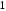 ; ; 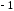 ; ; 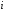 ; ; 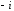 . .Задача 4. При каких действительных значениях x и y комплексные числа 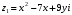 и и 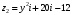 будут равны? будут равны?Решение: Комплексные числа 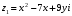 и и 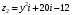 будут равны, если будут равны их действительные и мнимые части, т.е. выполняются условия: будут равны, если будут равны их действительные и мнимые части, т.е. выполняются условия: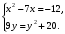 Так как каждое из равенств зависит от одной переменной, то необходимо решить каждое из равенств отдельно. Найдем решение первого уравнения 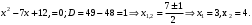 Найдем решение второго уравнения 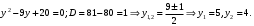 Следовательно, при 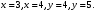 Ответ: 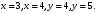 Задача 5. Найдите действительные значения xи y, если 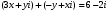 . .Решение: Преобразуем левую часть равенства, выделил мнимую и действительную часть 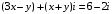 . .Составим и решим систему двух уравнений: 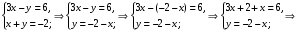 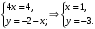 Ответ: 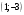 . .Задача 6. Решите уравнение 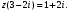 Решение: 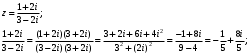 Следовательно, 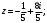 Ответ: 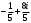 . .Задача 6. Даны комплексные числа 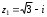 ; ; 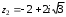 . Найдите значения следующих выражений: . Найдите значения следующих выражений:а) 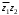 ; б) ; б) 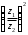 . .Решение: а) Число сопряженное числу 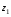 выглядит следующим образом: выглядит следующим образом: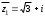 , следовательно, , следовательно,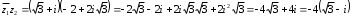 б) Число сопряженное числу 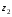 выглядит следующим образом: выглядит следующим образом: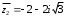 , следовательно, , следовательно,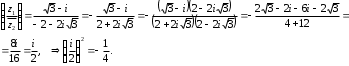 Ответ: а) Ответ: а) 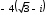 ; б) ; б) 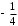 . .Задача 7. При каких действительных значениях x и y комплексные числа 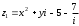 и и 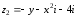 будут сопряженными? будут сопряженными?Решение: Данные комплексные числа 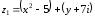 и и 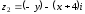 будут комплексно сопряженными, если их мнимые части будут разных знаков, т.е. выполняются условия: будут комплексно сопряженными, если их мнимые части будут разных знаков, т.е. выполняются условия: 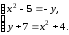 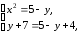 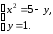 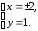 Ответ: 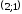 ; ; 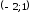 . .Задача 8. Решите во множестве комплексных чисел уравнение 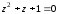 . .Решение Так как 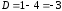 , тогда корни находятся по формуле , тогда корни находятся по формуле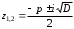 ( (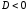 ). ).Отсюда следует, что 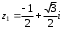 , , 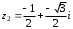 . .Ответ: 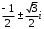 . .Задача 9. Найдите комплексные корни уравнения 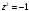 . .Решение: Так как 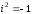 , то это данное уравнение можно представить следующим образом , то это данное уравнение можно представить следующим образом 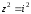 или или 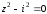 . Используя формулу сокращенного умножения – разность квадрата, представим левую часть как произведение множителей. Получаем . Используя формулу сокращенного умножения – разность квадрата, представим левую часть как произведение множителей. Получаем 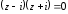 , следовательно, , следовательно, 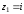 , , 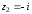 . .Ответ: 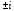 . . |
