рооо. Курсовая работа Комплексные числа. 2. Решение задач 17
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
2.2. Геометрическое представление комплексных чиселЗадача 1. Изобразите на комплексной плоскости, следующие комплексные числа: 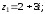 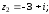 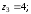 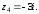 Решение: Каждому из этих комплексных чисел соответствуют точка комплексной плоскости. 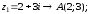 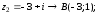 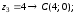 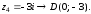 Изобразим на координатной плоскости. 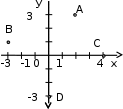 Рис.2.1.1. Задача 2. Изобразите графически множество всех точек комплексной плоскости, для которых выполняются следующие условия: а) 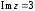 , б) , б) 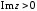 , в) , в) 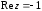 , г) , г) 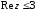 , д) , д) 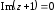 , , е) 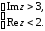 , ж) , ж) 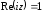 . .Решение а) 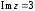 . Из соотношения . Из соотношения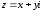 и и 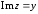 , получаем: , получаем: 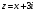 . .Множество точек – прямая 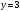 (рис. 2.2.2). (рис. 2.2.2). y 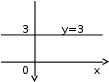 Рис. 2.2.2. б) 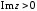 .Так как, .Так как, 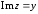 . Таким образом, . Таким образом, 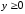 . .Множество точек – первой и четвертой координатных, включая прямую 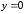 (рис. 2.2.3). (рис. 2.2.3).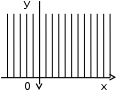 Рис. 2.2.3. в) 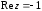 . Из равенств . Из равенств 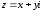 и и 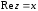 , следовательно: , следовательно: 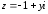 . .Множество точек – прямая 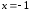 (рис. 2.2.4.). (рис. 2.2.4.).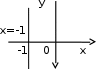 Рис. 2.2.4. г) 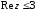 , Так как, , Так как, 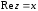 . Следовательно, . Следовательно, 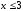 . .Множество точек – левая относительно прямой 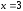 полуплоскость, включая прямую полуплоскость, включая прямую 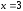 (рис. 2.2.5). (рис. 2.2.5). Рис. 2.2.5. д) 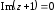 . . 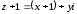 , поэтому , поэтому 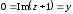 . . Множество точек – прямая 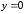 . (рис. 2.2.6). . (рис. 2.2.6).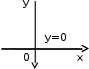 Рис. 2.2.6. е) 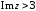 и и 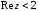 следовательно следовательно 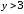 и и 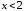 . Множество точек – часть плоскости, ограниченная снизу прямой . Множество точек – часть плоскости, ограниченная снизу прямой 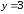 , справа , справа 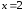 , исключая указанные прямые (рис. 2.2.7). , исключая указанные прямые (рис. 2.2.7).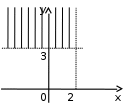 Рис. 2.2.7. ж) Так как 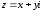 , то , то 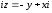 , и условие , и условие 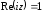 означает, что означает, что 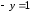 , следовательно , следовательно 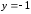 . Множество точек – прямая . Множество точек – прямая 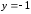 (рис. 2.2.7). (рис. 2.2.7).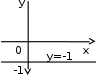 Рис. 2.2.7. Задача 3. Изобразите на координатной плоскости множество, всех точек 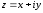 , удовлетворяющих условию: , удовлетворяющих условию:а) 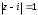 ; б) ; б) 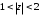 ; в) ; в) 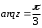 . .Решение: а) 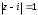 . Так как модуль означает расстояние, то число . Так как модуль означает расстояние, то число 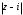 равно расстоянию между точкой равно расстоянию между точкой  и точкой и точкой 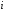 . Поэтому заданному условию . Поэтому заданному условию 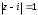 удовлетворяют точки, которые лежат на окружности радиуса 1 с центром в точке удовлетворяют точки, которые лежат на окружности радиуса 1 с центром в точке 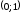 (рис. 2.2.8). (рис. 2.2.8).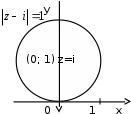 Рис. 2.2.8. б) 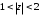 . Число . Число 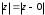 равно расстоянию между точкой равно расстоянию между точкой  и началом координат. Следовательно, условию и началом координат. Следовательно, условию 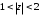 удовлетворяют точки, которые лежат между двумя окружностями с центром в начале координат и радиусами удовлетворяют точки, которые лежат между двумя окружностями с центром в начале координат и радиусами 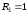 и и 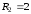 соответственно (рис. 2.2.9). соответственно (рис. 2.2.9).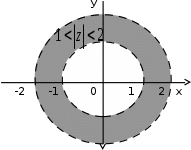 Рис. 2.2.9. в) 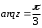 . Так как по определению аргумент комплексного числа -это угол между z и осью Ox, то . Так как по определению аргумент комплексного числа -это угол между z и осью Ox, то 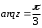 изображается следующим образом: изображается следующим образом: 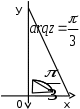 Рис. 2.2.10. |
