дисциплина. Дисциплина основы научных исследований. Измерения. Мамаев 2. Контрольная работа по дисциплине основы научных исследований Вариант 3 студент гр. Атхбпз201 Мамаев И. Д
 Скачать 104.55 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ» Филиал ТИУ в г. Сургуте Кафедра естественно-научных и гуманитарных дисциплин Контрольная работа по дисциплине основы научных исследований Вариант №3 Выполнил: студент гр. АТХбпз-20-1 Мамаев И.Д Проверил: Штанов Юрий Николаевич Сургут 2022 Оглавление Введение 1 Точность и погрешность измерений 1 Абсолютная и относительная погрешности 5 Причины погрешности и измерений 6 Виды измерительных устройств и класс точности 8 Влияние соотношения систематической и случайной погрешности на число измерений 9 Аналитическая обработка результатов измерений 12 Метод наименьших квадратов 14 Оценка погрешности метода наименьших квадратов 14 Корреляционный анализ 15 Регрессионный анализ 16 Проверка адекватности модели 17 Основная литература 19 Введение На современном этапе научно-технического прогресса необыкновенно возрастает роль средств, позволяющих рационально использовать ресурсы, выделенные для решения научно-технических задач. Кибернетика предлагает такие средства, как исследование операций, теория систем, математическое моделирование, теория эксперимента, вычислительная техника и др. Часть этих методов предназначена для увеличения эффективности научного эксперимента на всех стадиях разработки, исследования, проектирования и эксплуатации объектов. Единство теории и практики эксперимента совместно с вычислительной техникой образуют комплекс автоматизированного эксперимента, предназначенный для повышения производительности научного труда. Объекты, на которых проводятся эксперименты, отличаются, прежде всего, протекающими в них процессами. Точность и погрешность измеренийИзмерение — это определение значения измеряемой величины (сигнала) опытным путем, путем эксперимента, поставленного в конечном счете для преобразования измеряемого сигнала в форму, удобную для наблюдения и использования. Если через Х00 обозначить истинное значение измеряемого сигнала, то при идеальном преобразовании результат измерения может быть представлен в виде  где kп - коэффициент преобразования, постоянный во всем диапазоне изменения измеряемой величины и принимаемый за номинальное значение чувствительности канала измерения. В реальных условиях измерения выходной сигнал Y отличается от Y00 за счет непостоянства коэффициента преобразования, характеризуемого величиной ∆k, и за счет внешних и внутренних помех ∆Y1 приведенных к выходу. Поэтому реальное уравнение преобразования следует записать как, где ∆Y2=∆kX00— ошибка, вызванная непостоянством коэффициента преобразования; ∆Y — полная ошибка измерения, приведенная к выходу. Тогда ошибка ∆Х в определении измеряемой величины, или ошибка, приведенная ко входу, может быть определена из соотношения  Итак, погрешность измерения ∆X=X-X00, есть разность между полученным значением измеряемой величины и ее истинным значением. В дальнейшем X при ∆ будем опускать, т. е. будем писать ∆—Х=Х00. Так как истинное значение измеряемой величины не известно, то и определить точно погрешность измерения нельзя. Можно лишь оценить погрешность измерения, если за Х00 принять некоторое значение Х0, настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него. Это значение Х0 измеряемой величины называется действительным значением. Тогда оценка погрешности измерения ∆= Х –Х0. Погрешность измерения определяется погрешностями используемой измерительной аппаратуры; погрешностью метода (при косвенных измерениях); погрешностями, вызванными несогласованием входных параметров измерительной аппаратуры и выходных параметров цепи измеряемого сигнала; погрешностями, вызванными несоответствием инерционных свойств измерительной аппаратуры и скорости изменения измеряемого сигнала. Кроме того, оценка погрешности зависит от точности описания измеряемого сигнала x(t), т. е. от степени приближения действительного значения к истинному (в случае статических измерений — приближения Х0 к Х00). По характеру изменения погрешности измерения можно разделить на систематические и случайные. Систематические погрешности — это погрешности постоянные или изменяющиеся по некоторому закону, который может быть достаточно просто установлен путем постановки соответствующего эксперимента. При постановке эксперимента источники систематических ошибок должны быть но возможности исключены. Неисключенные систематические погрешности должны быть учтены путем введения в результат измерения поправок (исправленный результат измерения). Случайные погрешности — это погрешности, изменяющиеся от опыта к опыту и не поддающиеся непосредственному учету вследствие их хаотического изменения, обусловленного одновременным воздействием на результат измерения ряда различных, не зависимых друг от друга факторов. Наличие случайных погрешностей обнаруживается в том, что при многократном повторении измерения одной и той же величины в одинаковых условиях с одинаковой тщательностью результаты измерений несколько отличаются друг от друга. Случайные погрешности неизбежны. Поэтому следует считать недостаточно тщательными эксперименты, при повторении которых получаются совершенно одинаковые результаты. Следует заметить, что многие причины возникновения случайных ошибок нам известны (трение в опорах, неуравновешенность подвижных частей, порог чувствительности, дискретность и т. д.). Но от этого мало что меняется — погрешности, вызываемые ими, носят по-прежнему случайный характер. При исследовании результатов наблюдений среди случайных погрешностей может встретиться промах. Промах - это случайная погрешность, явно несоответствующая правильному результату измерения и свидетельствующая о грубой ошибке в постановке эксперимента, в отсчете. После установления промаха он должен быть исключен из результатов измерений. В общем случае погрешность результата имеет систематическую и случайную составляющие, даже если введены поправки на систематические погрешности, вызванные известными влияющими факторами. Объясняется это тем, что, во-первых, значения факторов не остаются в процессе измерения постоянными и, во-вторых, тем, что на результат измерения воздействуют факторы, действие которых в данном эксперименте не предполагалось, или факторы, действие которых невозможно учесть. Так как в погрешность измерения входит случайная составляющая, то ее следует считать случайной величиной. Очевидно, что указанные средине значения следует принять за систематические погрешности измерения в фиксированные моменты времени, а кривую, соединяющую их, следует считать зависимостью систематической погрешности от времени. Разность между погрешностью измерения и средним значением (систематической погрешностью) в каждом сечении следует рассматривать как случайные погрешности δ1k, δ2k,…,δik,…, δnk. Таким образом, случайная погрешность в момент измерения (например, tk) может принять любое из значений ∆ik. Значение полной погрешности измерения для любого момента времени будем записывать как ∆=θ+δ. Систематическая составляющая погрешности при обработке результатов измерений должна быть определена, и на нее, как уже говорилось, должен быть исправлен результат измерения (исправленный результат измерений), Точность измерения характеризуется случайной погрешностью. Определить ее можно аналитически и экспериментально. При аналитическом определении проводится анализ источников погрешностей измерительной аппаратуры, метода измерения и др., определяется характер погрешностей, их величина, взаимное влияние. По полученным данным, используя аппарат суммирования частных погрешностей случайного характера и частных погрешностей систематического характера, можно найти погрешность измерения в нормальных условиях и сделать указания о дополнительных (систематических) погрешностях, которые могут возникнуть при отклонении условий измерения от нормальных. Встает вопрос: можно ли утверждать, что рассчитанная на основании анализа погрешность измерения точно соответствует значению погрешности проведенного реального измерения? Конечно, нет. Путем анализа можно лишь оценить погрешность, так как нет возможности правильно учесть все факторы, определяющие погрешность измерения, и прежде всего законы распределения погрешностей и внешних факторов. Экспериментальный метод определения погрешности измерения требует статистических данных, т. е. многократного повторения измерения в одинаковых условиях с одинаковой тщательностью. Путем обработки статистических данных можно найти случайную погрешность отдельного измерения, наиболее достоверное значение измеряемой величины (действительное значение) и погрешность его определения, т. е. установить границы, в которых лежит истинное значение измеряемой величины, конечно, с некоторой доверительной вероятностью. Статистический метод следует рассматривать не только как метод определения погрешности измерения, но и как метод повышения точности измерения. Не следует думать, что полученная оценка погрешности отдельного измерения является незыблемой. При повторении того же эксперимента через некоторое время в тех же условиях, с той же тщательностью можно получить и несколько другую оценку погрешности. Абсолютная и относительная погрешностиА  бсолютная погрешность – это разница между измеренной датчиком величиной Хизм и действительным значением Хд этой величины.Абсолютная погрешность – это погрешность измерения, выраженная в единицах измеряемой величины. Наряду с абсолютной погрешностью часто используется термин абсолютное значение погрешности, под которым понимают значение погрешности без учета ее знака. Эти два понятия различны. Относительная погрешность – это погрешность измерения, выраженная отношением абсолютной погрешности к результату измерения. Для номинальной оценки погрешностей существует несколько правил: при сложении и вычитании чисел необходимо складывать их абсолютны погрешности; при делении и умножении чисел требуется сложить относительные погрешности; при возведении в степень относительную погрешность умножают на показатель степени. Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах. Причины погрешности и измеренийПо причине возникновения частные погрешности можно разделить на несколько групп: погрешности, вызванные несовершенством конструкции и технологии изготовления; погрешность градуировки (при индивидуальной градуировке) или шкаловая (при массовом производство); методические погрешности; погрешности, вызванные старением элементов; погрешности, вызванные влиянием внешних факторов; погрешности отсчета. Частные погрешности преобразователей носят случайный характер, т. е. величина их меняется случайным образом вне зависимости от значения измеряемой величины и условий работы. В большинстве случаев систематическую составляющую частной погрешности удается исключить путем корректировки в процессе изготовления измерительного устройства или перед его использованием. Исключение составляют такие аддитивные погрешности, как порог чувствительности, шумы, трение. Полностью исключить такого рода систематические погрешности на всем диапазоне измеряемой величины невозможно. На систематические погрешности, вызванные влиянием внешних факторов, могут быть внесены поправки, если изменение влияющего фактора может быть определено. Однако делается это, как правило, только при высокоточных измерениях в лабораторных условиях. Во всех других случаях поправка на погрешность, вызванную изменением условий работы, не вводится либо потому, что нет возможности производить необходимые расчеты, либо потому, что нет возможности следить за изменением фактора, особенно при его быстрых изменениях. Тогда систематическую погрешность переводят в разряд случайных и включают в полную погрешность прибора при нормировании его точности. Основными причинами возникновения погрешностей являются: несовершенство методов измерений, технических средств, применяемых при измерениях, органов чувств человека, условия проведения измерений. Все эти факторы влияют на суммарную погрешность измерения. Суммарную погрешность измерения можно разделить на две составляющие: систематическую и случайную погрешности. Систематические погрешности — это погрешности постоянные или изменяющиеся по некоторому закону, который может быть достаточно просто установлен путем постановки соответствующего эксперимента. При постановке эксперимента источники систематических ошибок должны быть но возможности исключены. Неисключенные систематические погрешности должны быть учтены путем введения в результат измерения поправок (исправленный результат измерения). Случайные погрешности относятся к непрерывным случайным величинам, т. е. они могут принимать несчетное множество значений. Перечислить все значения, записать их не представляется возможным. Поэтому, когда говорят о вероятности появления тех или иных погрешностей, имеют в виду вероятность Р того, что погрешность либо будет меньше некоторого значения P(∆<∆ Случайные погрешности — это погрешности, изменяющиеся от опыта к опыту и не поддающиеся непосредственному учету вследствие их хаотического изменения, обусловленного одновременным воздействием на результат измерения ряда различных, не зависимых друг от друга факторов. Наличие случайных погрешностей обнаруживается в том, что при многократном повторении измерения одной и той же величины в одинаковых условиях с одинаковой тщательностью результаты измерений несколько отличаются друг от друга. Случайные погрешности неизбежны. Поэтому следует считать недостаточно тщательными эксперименты, при повторении которых получаются совершенно одинаковые результаты. Следует заметить, что многие причины возникновения случайных ошибок нам известны (трение в опорах, неуравновешенность подвижных частей, порог чувствительности, дискретность и т. д.). Но от этого мало что меняется — погрешности, вызываемые ими, носят по-прежнему случайный характер. При исследовании результатов наблюдений среди случайных погрешностей может встретиться промах. Промах - это случайная погрешность, явно несоответствующая правильному результату измерения и свидетельствующая о грубой ошибке в постановке эксперимента, в отсчете. После установления промаха он должен быть исключен из результатов измерений. В общем случае погрешность результата имеет систематическую и случайную составляющие, даже если введены поправки на систематические погрешности, вызванные известными влияющими факторами. Объясняется это тем, что, во-первых, значения факторов не остаются в процессе измерения постоянными и, во-вторых, тем, что на результат измерения воздействуют факторы, действие которых в данном эксперименте не предполагалось, или факторы, действие которых невозможно учесть. Виды измерительных устройств и класс точностиИзмерительным прибором называется устройство, с помощью которого измеряемая величина сравнивается с единицей измерения. Измерительный прибор предназначен для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительные приборы делятся на образцовые и рабочие. Образцовыми называются приборы, предназначенные для хранения и воспроизводства единиц измерения, а также для проверки и градуировки приборов. Рабочими называются приборы, используемые для практических измерений. В свою очередь, рабочие измерительные приборы делятся на лабораторные и технические. Лабораторные приборы в промышленности не применяют и в связи с этим далее они не рассматриваются. Для автоматического контроля и регулирования в промышленности используют технические рабочие приборы. Влияние соотношения систематической и случайной погрешности на число измеренийВоздействие помех на процесс измерения приводит к тому, что результаты измерения всегда отличаются от истинного значения измеряемой величины и по этим результатам определить истинное значение нельзя. Разность между результатом измерения и истинным значением называется истинной погрешностью измерения. В силу того что истинное значение неизвестно, неизвестной является и истинная погрешность. Учитывая, что ни истинное значение физической величины, ни истинную погрешность в опыте определить невозможно, задачу нахождения истинного значения формулируют как задачу нахождения некоторого приближенного к истинному значения с указанием диапазона возможных отклонений этого приближенного значения от истинного. Найденное в эксперименте значение измеряемой величины, приближенное к истинному, называется оценкой физической величины. Оценка с указанием ее возможного интервала отклонения от истинного значения называется результатом измерения. Погрешность измерения включает в себя множество различных составляющих, которые можно классифицировать по различным признакам. В настоящее время классификация погрешностей содержит около 30 видов. Измерения можно разделить по виду влияния на результаты – на систематические и случайные; по характеру изменения во времени – на статические и динамические; по источникам возникновения – на методические, инструментальные, погрешности оператора, которые, в свою очередь, могут быть как случайными, так и систематическими; по возможности выявления и исключения из результатов измерения – на выявленные и невыявленные, устранимые и неустранимые, исключенные и неисключенные; по характеру принадлежности (близости) результатов наблюдений к основной совокупности выделяют грубые погрешности и промахи. Невыявленная погрешность всегда неустранима. Выявленная погрешность может быть как устранимой, так и неустранимой. Так, случайная погрешность, а также систематическая погрешность известной величины, но неизвестного знака, имеют определенные числовые значения, т. е. относятся к разряду выявленных. Тем не менее, они не могут быть устранены (исключены из результатов), т. е. являются неустранимыми. Далее приведены определения основных видов погрешностей. Систематическая погрешность – это составляющая погрешности измерения, которая остаётся постоянной или закономерно изменяется при повторных измерениях. Одной из основных задач обработки результатов эксперимента является выявление, оценка величины и, по возможности, устранение всех систематических погрешностей. Изменяющиеся систематические погрешности выявляются легче постоянных. Для выявления постоянной систематической погрешности необходимо выполнить измерения хотя бы двумя различными способами или методами. Обнаруженные и оцененные систематические погрешности исключаются из результатов путем введения поправок. В зависимости от причин возникновения систематические погрешности подразделяют на следующие виды: 1. Погрешности метода или модели, которые обычно называют методическими погрешностями, например: определение плотности вещества без учета имеющихся в нем примесей, использование формул, не совсем точно описывающих явление, и др. 2. Погрешности воздействия внешних факторов: внешних тепловых, радиационных, гравитационных, электрических и магнитных полей. 3. Погрешности, возникающие из-за неточности действий или личных качеств оператора (экспериментатора), называемые личностными погрешностями. 4. Инструментальные (приборные, аппаратурные) погрешности, обусловленные схемными, конструктивными и технологическими несовершенствами средств измерения, их состоянием в процессе эксплуатации. Например, смещение начала отсчета, неточность градуировки шкалы прибора, использование прибора вне допустимых пределов его эксплуатации, неправильное положение прибора и т. п. За исключением смещения начала отсчета, приборные погрешности относятся к разряду неустранимых погрешностей. В общем случае систематическая погрешность обусловлена суммарным воздействием перечисленных факторов, многие из которых невозможно рассчитать, подавить или выявить в данном эксперименте. Самым простым способом выявления суммарной систематической погрешности было бы сопоставление результатов измерений, полученных с помощью серийного (рабочего) и более точного образцового приборов. Разность результатов измерений даст суммарную систематическую погрешность, вносимую серийным прибором в результат измерения. Однако такой способ выявления систематической погрешности является слишком дорогим. Поэтому на практике различные составляющие систематической погрешности пытаются устранить с помощью экспериментальных или математических приемов путем введения поправок в результаты наблюдений при условии, что погрешность данного вида по величине и знаку известна. После внесения поправок влияние систематической погрешности данного вида на результат и погрешность измерения устраняется полностью. Если же систематическая погрешность неизвестна, но имеет известные границы изменения, то её учитывают в результате измерения. Относительная и приведенная погрешности являются безразмерными величинами и, как правило, выражаются в процентах. Одни составляющие погрешности могут быть устранены из результатов измерений, а другие – нет. Все виды неустранимых погрешностей вносят вклад в полную погрешность измерения, и для ее нахождения должны быть просуммированы по определенным правилам, которые будут рассмотрены в дальнейшем. Аналитическая обработка результатов измеренийПусть при выполнении определенных условий происходит некоторое событие, которое будем называть "событием А". Каждый случай выполнения этих условий принято называть опытом или испытанием. Возможны три ситуации: 1. Событие А происходит всякий раз при осуществлении опыта или испытания. Такое событие называется достоверным. 2. Событие не происходит никогда (ни в одном испытании). Такое событие называется невозможным. 3. В каждом данном испытании событие А может произойти, но может и не произойти, причем точно указать, в каком испытании оно произойдет, а в каком – нет, заранее невозможно. Такое событие называют случайным, исход испытания также является случайным. Предсказание исхода того или иного испытания (произойдёт или не произойдет событие А в данном испытании) основывается на накопленном опыте. Для ситуаций 1 и 2 можно дать точное предсказание исхода будущего испытания. В ситуации 3 предсказание можно сделать лишь грубо ("в среднем"), указав, что событие может произойти лишь в такой-то доле от общего числа испытаний. Несмотря на случайность исходов отдельных испытаний, при многократном их повторении мы можем наблюдать вполне определенные средние результаты. Тенденция стремления результатов испытаний к некоторому общему среднему результату при увеличении числа испытаний получила название статистической устойчивости, существование которой основывается на предшествующем опыте или интуиции. Классическим примером являются опыты с подбрасыванием монеты. Выпадение герба при падении монеты в разных сериях испытаний происходит в числе испытаний, близком к половине общего их числа в серии. При увеличении числа испытаний в серии число выпадений герба всё больше приближается к половине общего числа испытаний в серии, т. е. к некоторому неслучайному показателю. Пусть в N испытаниях событие А произошло n(А) раз. Отношение n(А)/N называется относительной частотой или просто частотой появления события А. Если провести несколько серий опытов по N испытаний в каждой, то отношение n(A)/N будет различным для разных серий, но при увеличении N это отношение будет стремиться к некоторому постоянному числу, называемому вероятностью появления события А: n(A)/N → Р(А) при N →∞ . Вероятность является объективной характеристикой и математическим выражением возможности появления случайного события А в каждом отдельном испытании. Нетрудно видеть, что вероятность принимает значения, лежащие в интервале от нуля до единицы, т. е. 0 ≤ Р(А) ≤ 1, причем для достоверного события Р(А) = 1 (n(А) = N), для невозможного события Р(А) = 0 (n(А) = 0). Физическое содержание события А может быть различным. Таким событием может быть выпадение герба при бросании монеты, рождение мальчика или девочки, превышение температурой воздуха заданного уровня в течение выбранных суток и др. В большинстве случаев имеют место не отдельные события, а их комбинации, в связи с чем встают вопросы определения вероятностей этих комбинаций на основе знания вероятностей отдельных событий или других комбинаций этих же событий. Если появление одного из событий делает невозможным появление других в данном испытании, то такие события называются несовместимыми. Если в каждом испытании должно обязательно произойти одно из событий некоторой группы, то эти события образуют полную группу. Если события к тому же несовместимы, то они образуют полную группу несовместимых событий. Пусть события А1, ..., AN образуют полную группу и несовместимы. Тогда появление любого из этих событий в данном испытании есть достоверное событие, вероятность которого равна единице, то есть P(A1 или А2, ... или АN) = 1 ( ) 1 N k k P A = ∑ = . Если же вероятности этих событий равны между собой, то 1 ( ) ( ) 1, N k k k P A NP A = ∑ = = откуда ( ) 1/ P A N k = . Классическим примером рассмотренной ситуации является выпадение некоторого числа очков при бросании игральной кости, представляющей собой кубик с цифрами 1, 2, 3, 4, 5, 6, нанесенными на гранях. Выпадение каждой грани является случайным событием. Если кубик считать идеальным, то вероятности выпадения всех граней одинаковы. Выпадение одной из них исключает выпадение других, и события, состоящие в выпадении 1...6 очков, образуют полную группу несовместимых событий. Вероятность выпасть любому из указанных чисел равна 1/6. Вероятность получить число очков не менее 3 при одном бросании равна вероятности выпадения чисел 3, 4, 5, 6, т. е. (1/6)4 = 2/3. М |
етод наименьших квадратов
ля этого требуется вычислить суммы квадратов отклонений исходных данных от этих линий и , меньшее значение соответствует линии, которая лучше в смысле метода наименьших квадратов аппроксимирует.
, то прямая y = 0.165x+2.184 лучше приближает исходные данные.
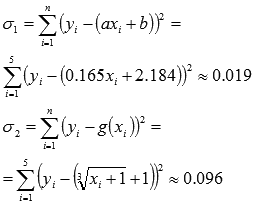
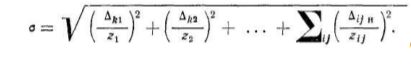огрешностей прибора