Контрольная работа. Основы теории надежности. Контрольная работа по дисциплине Основы теории надежности Барнаул 2019 г. Содержание зач кн 7
 Скачать 166 Kb. Скачать 166 Kb.
|
|
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВАРОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ» Факультет Заочного обучения Кафедра: Технологии конструкционных материалов и ремонта машин Контрольная работа по дисциплине: «Основы теории надежности» Барнаул 2019 г. СОДЕРЖАНИЕЗач.кн 7. стр. Вопрос № 7. Вероятность безотказной работы. Вероятность отказов. Определение и расчет показателей……………………………………… 3 Вопрос № 12. Усталостные разрушения, причины и последствия…….. 7Вопрос № 17. Процесс восстановления деталей ………………………. 11Список Литературы ……………………………………………………… 16 Вопрос №7. Вероятность безотказной работы. Вероятность отказов. Определение и расчет показателей. Вероятностью безотказной работы оборудования - называется вероятность того, что она будет сохранять свои характеристики (параметры) в заданных пределах в течение определенного промежутка времени при определенных условиях эксплуатации, или, короче, – вероятностью безотказной работы аппаратуры называется вероятность того, что в определенных условиях эксплуатации в пределах заданной продолжительности работы отказ не возникает. В дальнейшем эта характеристика обозначается P(t). Вероятность отказа - это вероятность того, что при определенных условиях эксплуатации в заданном интервале времени произойдет хотя бы один отказ. Обозначается как Q(t). Пусть t – время, в течение которого необходимо определить вероятность безотказной работы, а Т1 – время работы аппаратуры от ее включения до первого отказа. Тогда, согласно определению вероятности безотказной работы, справедливо выражение: т.е. вероятность безотказной работы – это вероятность того, что время Т1 от момента включения аппаратуры до ее отказа будет больше или равно времени t, в течение которого определяется вероятность безотказной работы. Из определения вероятности безотказной работы видно, что эта характеристика является функцией времени. Она имеет следующие очевидные свойства: 1) P(t) является убывающей функцией времени; 2) 3) Р(0) = 1, На практике для определения P(t) из статистических данных об отказах аппаратуры обычно используются методы непосредственного подсчета вероятностей. Вероятность безотказной работы определяется следующей статистической оценкой: где N0 – число образцов аппаратуры в начале испытания, n(t) – число отказавших образцов за время t. При увеличении числа образцов N0 статистическая оценка На практике иногда более удобной характеристикой является вероятность неисправной работы, или вероятность отказов. Эта характеристика может быть полезна, например, при сравнение надежности резервированной и не резервированной систем. Исправная работа и отказ являются событиями несовместными и противоположными. Поэтому вероятность безотказной работы и вероятность отказа Q(t) связаны зависимостью: Q (t) = 1 – P (t), (1.4) или с учетом выражения (1.1) Q (t) = P (T1 Из выражения (1.5) видно, что вероятность отказа является интегральной функцией распределения времени работы (Т1) до отказа, т.е. Q (t) = F (t) (1.6) Производная от интегральной функции распределения есть дифференциальный закон (плотность) распределения: Тогда на основании выражений (1.6) и (1.7) получим: т.е. производная от вероятности отказа подчиняется дифференциальному закону распределения времени работы (Т1) аппаратуры до ее отказа. Для статистического определения вероятности отказа воспользуемся выражениями (1.4)и (1.3). Подставляя в выражение (1.4) вместо P(t) его выражение из формулы (1.3), получим: Вероятность безотказной работы P(t), как количественная характеристика надежности, обладает следующими достоинствами: 1) характеризует изменение надежности во времени; 2) входит во многие другие характеристики аппаратуры, а поэтому может быть полезна широкому кругу лиц, занимающихся вопросами проектирования, эксплуатации, ремонта и т.п. Например, вероятность безотказной работы наряду с точностью и живучестью определяет боевую эффективность оружия, а поэтому является необходимой для исследователя военных операций и полководца. Она определяет также стоимость изготовления и эксплуатации аппаратуры, а поэтому может быть полезной инженеру-экономисту; 3) охватывает большинство факторов, существенно влияющих на надежность аппаратуры, и поэтому достаточно полно характеризует надежность; 4) может быть сравнительно просто получена расчетным путем до изготовления системы. Это позволяет выбрать оптимальную в смысле надежности структуру системы и ее принципиальную схему; 5) является удобной характеристикой надежности, как простейших элементов, так и сложных систем и даже комплексов. Указанные достоинства вероятности безотказной работы явились причиной наибольшего распространения этой характеристики. Однако вероятность безотказной работы имеет также существенные недостатки: 1) характеризует надежность восстанавливаемых систем только до первого отказа, а поэтому является достаточно полной характеристикой надежности только систем разового использования; 2) не позволяет охарактеризовать зависимость между временными составляющими цикла эксплуатации; это не дает возможности установить, даже в вероятностном смысле, будет ли система готова к действию в данный момент времени или нет; 3) не всегда удобна для оценки надежности простых элементов, в особенности таких, у которых отсутствует старение; 4) по известной вероятности безотказной работы бывает трудно вычислить другие количественные характеристики надежности. Эти недостатки позволяют сделать вывод, что вероятность безотказной работы, как, впрочем, и любая другая характеристика, не полностью характеризует такое свойство как надежность, и поэтому не может быть с ним отождествлена. _________________________________________1 Зубарев Ю.Н. Основы надежности машин и сложных систем Учебник для ВУЗов. М.Колос 2017 г. - 221стр. Вопрос №12. Сохраняемость. Определение и показатели. Сохраняемость - свойство объекта сохранять значение показателей безотказности, долговечности и ремонтопригодности после хранения и транспортирования. Практическая роль этого свойства особенно велика для приборов. Сохраняемость - характеризуется его способностью противостоять отрицательному влиянию условий и продолжительности хранения и транспортирования на его безотказность, ремонтопригодность и долговечность. Сохраняемость представляют в виде двух составляющих, одна из них проявляется во время хранения, а другая - во время применения объекта после хранения и/или транспортирования. Показателями сохраняемости являются: гарантированный срок сохраняемости; средний срок сохраняемости; гамма-процентный срок сохраняемости; медианный срок сохраняемости и др. Показатели сохраняемости дают количественную характеристику способности прибора сохранять безотказность и другие показатели качества при хранении и транспортировке в определенных условиях. Такими показателями являются, например, коэффициент сохранения безотказности и коэффициент сохраняемости. Коэффициент сохранения безотказности - определяется соотношением вероятности безотказной работы нового прибора в течение некоторого времени (или наработки) t0 после хранения и транспортировки Pi(t0) к этой же вероятности до хранения и транспортировки P0(t0):  Коэффициент сохраняемости - определяется по следующей формуле:  где Q“, Q' — значения независимых показателей качества прибора (например, точности, дальности действия, мощности и т. д.) до и после его хранения и транспортирования; Qifl0U — предельно допустимое значение этих показателей. Сроком сохраняемости - называется календарная продолжительность хранения и (или) транспортирования изделия в заданных условиях, в течение и после которой значения показателей качества остаются в установленных пределах. Показатели сохраняемости оценивают статистическими методами по результатам испытаний. Средним сроком сохраняемости - технического изделия называется математическое ожидание его срока сохраняемости. Средний срок сохраняемости определяют по формуле  где Tci — срок сохраняемости i-ro изделия; N — число однотипных изделий. Назначенный срок хранения есть календарная продолжительность хранения в заданных условиях, по истечении которой применение изделия по назначению не допускается независимо от его технического состояния. Гамма-процентный срок сохраняемости — это срок сохраняемости, достигаемый изделием с заданной вероятностью у, выраженной в процентах. Можно также сказать, что это минимальный срок сохраняемости, который будут иметь у процентов изделий данного вида. Вопрос №17. Коэффициент вариации информационного ряда и его влияние на выбор закона распределения. Коэффициент вариации - это относительная характеристика случайной величины, используется при выборе теоретического закона распределения. Идентификация случайных последовательностей, нестационарных случайных процессов и их производных по первым реализациям динамического ряда обусловливает необходимость введения в рассмотрение выборочного распределения коэффициента вариации. Коэффициентом вариации (коэффициентом изменчивости выборки) является отношение где 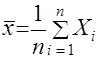 и и 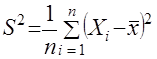 – среднее значение и дисперсия выборки соответственно. – среднее значение и дисперсия выборки соответственно.Гауссово распределение не обладает тем свойством, что случайная величина может принимать только положительные значения, однако если В этом случае  , ,  , (14) , (14)где Величина 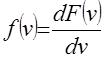 . .Не нарушая общности рассуждений и с целью использования зависимости (2) определим плотность распределения величины, обратной выборочному коэффициенту вариации 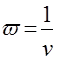 , для выборки , для выборки Если каждая из независимых величин 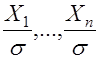 независимы и нормальны (0,1). Таким образом, плотность вероятности величины независимы и нормальны (0,1). Таким образом, плотность вероятности величины  . (15) . (15)Среднее арифметическое 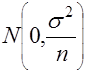 . .Поэтому можно показать, что плотность 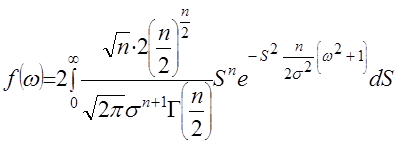 . (16) . (16)При 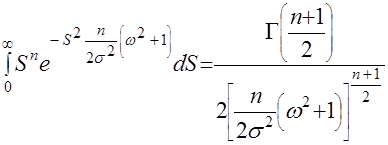 (17) (17)При 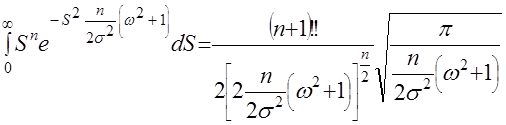 . (18) . (18)После соответствующих преобразований плотность распределения величины  . (19) . (19)Учитывая, что 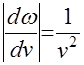 , получаем следующий результат. , получаем следующий результат.Теорема 5. Пусть имеет вид  . (20) . (20)Теоретический закон распределения (ТЗР) выражает общий характер изменения показателя надежности и исключает частные отклонения, связанные с недостатком первичной информации, т.е. ТЗР характеризует генеральную совокупность. Опытное распределение имеет частные особенности, которые должны быть исключены при переносе характеристик опытного распределения на генеральную совокупность. Процесс замены опытных закономерностей теоретическими называется выравнивание опытной информации. Каждый ТЗР характеризуется двумя функциями: f(t) - дифференциальная функция; F(t) - интегральная функция. Применительно к показателям надежности машин, эксплуатируемых в сельском хозяйстве, в подавляющем большинстве случаев используется закон нормального распределения (ЗНР) и закон распределения Вейбулла (ЗРВ). Выбор теоретического закона производится исходя из следующих признаков: По величине коэффициента вариации: если V < 0,3 - выбирается ЗНР; если 0,3 < V < 0,5 - выбирается ЗНР или ЗРВ; если V > 0,5 - выбирается ЗРВ. По области применения. ЗНР применяется, как правило при определении характеристик рассеивания: ресурсов и сроков службы машин и агрегатов; времени и стоимости восстановления работоспособности машин; наработка на ресурсный отказ; ошибок измерений размеров деталей. б) ЗРВ применяется, как правило, при определении: ресурсов и сроков службы отдельных деталей и сопряжений; доремонтных и межремонтных ресурсов тех элементов машин, отказы которых вызваны выходом из строя одной и той же детали; информации по износам деталей. Здесь применим закон нормального распределения и закон распределения Вейбулла. Закон нормального распределения (ЗНР) Отличительной особенностью ЗНР является симметричное рассеивание частных значений относительного среднего. _________________________________________3 Обеспечение надежности сложных технических систем [Электронный ресурс]: учебник/А.Н.Дорохов – Спб: Лань, 2010, 352 с.Список литературыЗубарев Ю.Н. Основы надежности машин и сложных систем Учебник для ВУЗов. М.Колос 2017 г. - 221стр. Надежность и ремонт машин. В.В Курчаткин, Н.Ф. Тельнов, К.А. Ачкасов и др. Под.ред. В.В Курчаткина – М:Колос, 2000 г. Обеспечение надежности сложных технических систем [Электронный ресурс]: учебник/А.Н.Дорохов – Спб: Лань, 2010, 352 с. |
