Контрольная работа планирование эксперимента в электроэнергетике. Контрольная работа по дисциплине "Планирование эксперимента в электроэнергетике и электротехнике"
 Скачать 177.76 Kb. Скачать 177.76 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования “Ивановский государственный энергетический университет им. В.И. Ленина” Кафедра ЭСПиДЭ Контрольная работа по дисциплине “Планирование эксперимента в электроэнергетике и электротехнике” Вариант 8 Выполнил: студент группы 3-70к Белов А.Р Шифр 918018 Проверил: старший преподаватель Страхов А.С Иваново 2021 ЗаданиеСоставить математическую модель зависимости разрядного напряжения штыревого фарфорового изолятора от давления, абсолютной влажности и температуры окружающей среды. В модели учесть взаимные и общее влияния атмосферных условий. Результаты серии экспериментов представлены в табл.1. Выполнить оценку полученной математической модели с учетом дополнительных экспериментов, выполненных в центре плана: 50,3кВ, 51,2кВ, 50,9кВ, 51,3 кВ, 51 кВ. 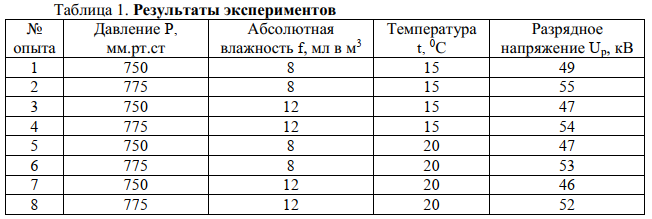 По полученной модели определить значение разрядного напряжения при следующих условиях: давление – 762 мм рт. ст., абсолютная влажность 11мл в м3и температура 17 °С. РешениеПо условию задачи на разрядное напряжение (параметр оптимизации y) влияют 3 фактора: давление (x1); абсолютная влажность (x2); температура (x3). Каждый из факторов в серии экспериментов варьируется на двух уровнях. Поэтому данный эксперимент можно обозначить как ПФЭ 23. Математическая модель для ПФЭ 23, в которой необходимо учесть взаимные и общее влияния факторов, имеет вид: 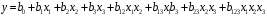 Для выполненной серии экспериментов составим матрицу планирования с учетом всевозможных эффектов взаимодействия.
Для упрощения расчетов определим неизвестные коэффициенты b0, b1, b2, b3, b12, b13, b23, b123 математической модели относительно кодированных значений факторов (Х1, Х2,Х3): 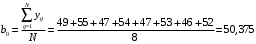 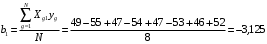 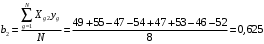 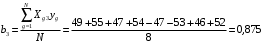 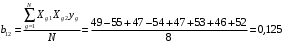 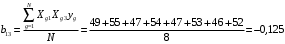 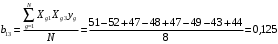 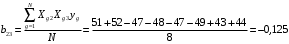 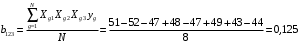 Подставляя полученной данные в математическую модель, получим: 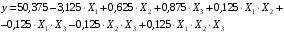 Выполним оценку полученной модели. Среднее значение параметра оптимизации в центре плана 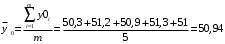 Дисперсия воспроизводимости: 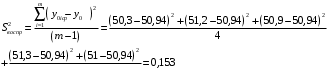 Дисперсия определения коэффициентов модели 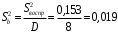 Критерии Стьюдента для коэффициентов модели 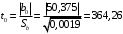 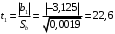 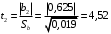 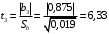 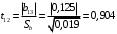 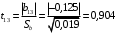 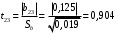 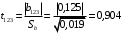 При числе степеней свободы 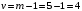 и уровне значимости и уровне значимости 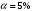 табличное значение критерия Стьюдента составит табличное значение критерия Стьюдента составит 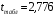 . .Поскольку 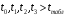 , a , a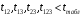 , то можно принять гипотезу о незначимости коэффициентов , то можно принять гипотезу о незначимости коэффициентов 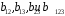 для данной модели. Значит, можно исключить коэффициенты для данной модели. Значит, можно исключить коэффициенты 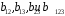 из модели: из модели: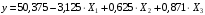 Для проверки содержательности модели или ее предсказательной способности необходимо определить отношение дисперсии относительно среднего значения отклика и остаточной дисперсии. Дисперсия относительно среднего значения отклика составит 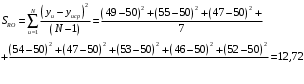 Остаточная дисперсия находится как 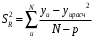 , ,где p – количество коэффициентов bв модели (равно 4). 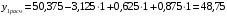 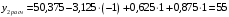 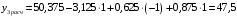 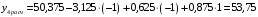 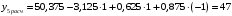 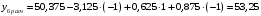 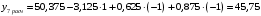 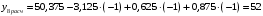 Остаточная дисперсия составит 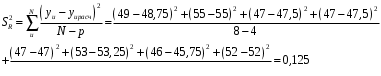 Отношение 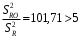 , ,значит, составленную модель можно считать содержательной. Расчетное значение коэффициента Фишера 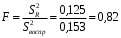 Табличное значение коэффициента Фишера при уровне значимости 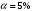 и числе степеней свободы для числителя и числе степеней свободы для числителя 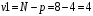 и знаменателя и знаменателя 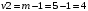 равно равно 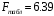 . .Поскольку 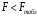 , то модель является адекватной. , то модель является адекватной.Так как коэффициенты b0, b1, b2, b3 были определены относительно кодированных значений факторов (Х1, Х2, Х3), то для составления математической модели необходимо перейти к расчету относительно натуральных значений факторов. Основные уровни факторов составят: 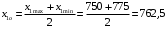 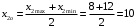 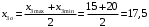 Кодированные и натуральные значения факторов связаны через выражения 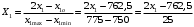 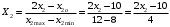 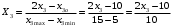 Подставляя полученные данные в математическую модель, получим 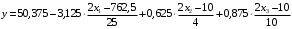 Модель с учетом обозначений по условию задачи примет вид 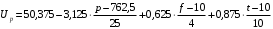 Вычислим по полученной модели значение разрядного напряжения при следующих условиях: давление – 762 мм рт. ст., абсолютная влажность 11 мл в м3 и температура 17°С. 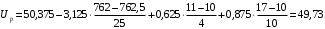 |
