задачи микро. задачи по эластичности. Практическая работа 2 Целью данного практикума является усвоение методики расчета коэффициентов эластичности и их применения на практике
 Скачать 143 Kb.
|
|
Раздел 1. Исходные основы микроэкономики Тема 2. Эластичность спроса и предложения Практическая работа 2
Оглавление Раздел 1. Исходные основы микроэкономики 1 Тема 2. Эластичность спроса и предложения 1 Практическая работа 2 1 Оглавление 1 Задачи на расчет коэффициентов эластичности 1 Задача 1 1 Задача 2 2 Задача 3 3 Задача 4 3 Задача 5 4 Задача 6 5 Задача 7 5 Задача 8 6 Задача 9 6 Задача 10 6 Задачи на использование коэффициентов эластичности 7 Задача 11 7 Задача 12 7 Задача 13 7 Задачи на расчет коэффициентов эластичности Задача 1 Постановка задачи: Рассмотрите рисунок. Определите коэффициент ценовой эластичности на отрезке АВ кривой спроса d1. О каком товаре идет речь? 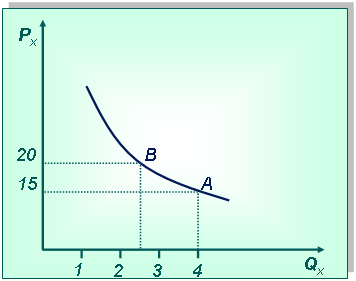 Технология решения задачи: Для решения задачи необходимо вспомнить, как определяется дуговой коэффициент ценовой эластичности. Коэффициент эластичности обозначим Еd/p, тогда 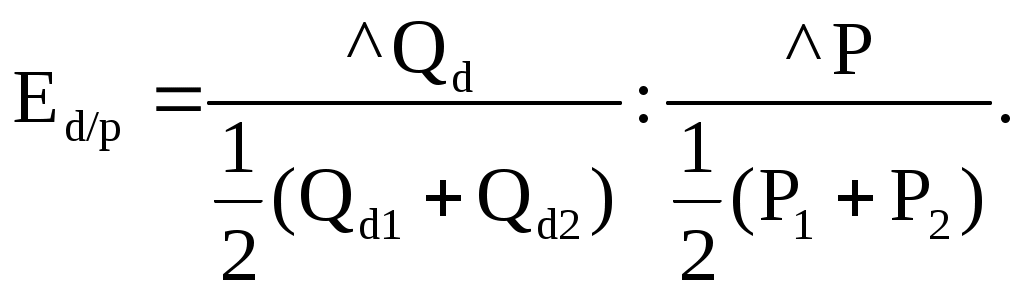 Поставив в формулу значения, получим:  Этот коэффициент характеризует эластичный товар. Ответ: коэффициент эластичности равен –2,3. Товар эластичен. Задача 2 Постановка задачи: Даны три товара. Изменения объемов спроса в зависимости от изменения цены приведены в таблице. Определите коэффициенты ценовой эластичности по каждому товару.
Технология решения задачи: необходимо определить коэффициенты дуговой эластичности спроса по цене по каждому товару. Коэффициент эластичности товара А (Еd/p A) определяется по формуле 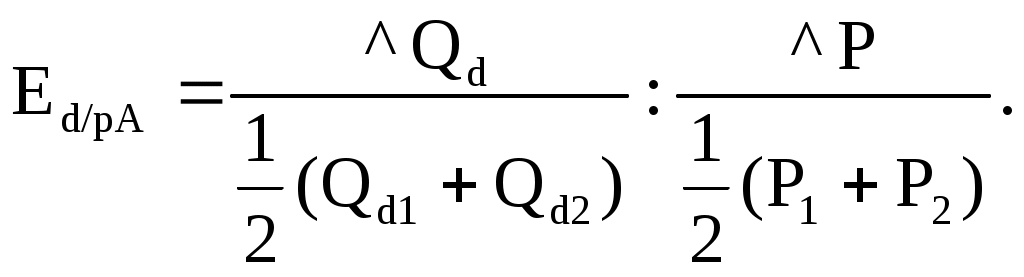 Поставив в формулу значения, получим:  Этот коэффициент характеризует эластичный товар. Аналогично рассчитаем коэффициент эластичности по товару В:  И, наконец, Еd/p C:  Ответ: Еd/p A= –1,25; Еd/p B= –1; Еd/p C= –0,6. Задача 3 Постановка задачи: В результате роста цены с 4 до 7 долл., объем спроса на товар Х упал с 1000 до 800 штук. Определите коэффициент эластичности спроса по цене. Технология решения задачи: Коэффициент эластичности обозначим Еd/р, тогда 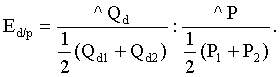 Поставив в формулу значения, получим: 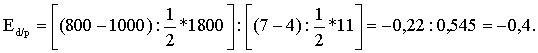 Этот коэффициент характеризует малоэластичный товар. Ответ: коэффициент эластичности равен –0,4; это малоэластичный товар. Задача 4 Постановка задачи: Цена на товар А выросла со 100 до 200 ден. ед. Спрос на этот товар упал с 3000 до 1000 штук. Спрос на товар В вырос с 500 до 1000. Определите коэффициенты эластичности товара А и В. О каких коэффициентах идет речь? Технология решения задачи: Так как цена товара А выросла, а спрос на этот товар упал, то можно определить коэффициент ценовой эластичности товара А:  Поставив в формулу значения, получим: 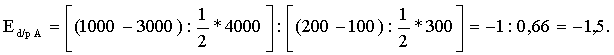 Реакцию спроса товара В на изменение цены товара А показывает коэффициент перекрестной эластичности, который определяется по формуле 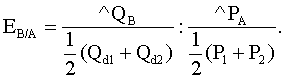 Подставим значения и получим: 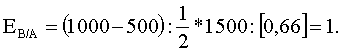 Поскольку коэффициент положительный, то речь идет о товарах, взаимозаменяющих друг друга. Ответ: коэффициент ценовой эластичности товара А составляет (–1,5), коэффициент перекрестной эластичности +1. Задача 5 Постановка задачи: Цена на товар А выросла со 10 до 15 ден. ед. Спрос на товар В вырос с 1000 до 2000 штук, на товар С упал с 50 до 40 кг. Определите коэффициенты перекрестной эластичности. Технология решения задачи: Сначала рассчитываем коэффициент перекрестной эластичности товара В по формуле 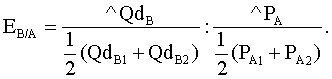 Подставим значения и получим: 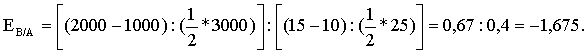 Поскольку коэффициент положительный, то речь идет о товарах, взаимозаменяющих друг друга. Затем определяем коэффициент перекрестной эластичности товара С по такой же формуле: 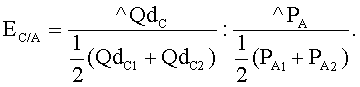 Подставим значения и получим:  Поскольку коэффициент отрицательный, то речь идет о товарах, взаимодополняющих друг друга. Ответ: ЕB/A= 1,675; ЕC/A= –0,56. Задача 6 Постановка задачи: Цена на товар А выросла со 1 до 4 ден. ед. Спрос на товар В упал с 3000 до 1000 штук. Спрос на товар С вырос с 500 до 1000, на товар Д не изменился. Определите коэффициенты перекрестной эластичности. Технология решения задачи: Сначала рассчитываем коэффициент перекрестной эластичности товара С по формуле 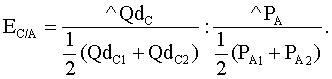 Подставим значения и получим: 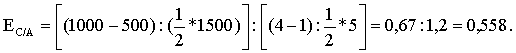 Поскольку коэффициент положительный, то речь идет о товарах, взаимозаменяющих друг друга. Затем определяем коэффициент перекрестной эластичности товара В по такой же формуле: 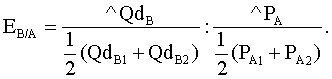Подставим значения и получим: 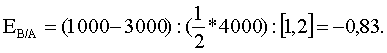 Поскольку коэффициент отрицательный, то речь идет о товарах, взаимодополняющих друг друга. Поскольку спрос на товар Д не изменился, коэффициент перекрестной эластичности равен 0, т. е. товары являются нейтральными. Ответ: ЕB/A =–0,83; ЕC/A = 0,558; ЕД/A = 0. Задача 7 Постановка задачи: На рынке товара А объем спроса определяется формулой  . Определите эластичность спроса в точке, соответствующей Q = 10. Технология решения задачи: Для решения задачи необходимо применить формулу расчета коэффициента точечной эластичности:  , где B – коэффициент, показывающий угол наклона кривой спроса. Сначала надо найти цену:  , следовательно, Р = 4. Отсюда  .Ответ: коэффициент эластичности равен 0,8. Задача 8 Постановка задачи: Спрос на товар Х определяется формулой  . Определите коэффициент эластичности при цене, равной 30 у. е. Технология решения задачи: Для решения задачи необходимо применить формулу расчета коэффициента точечной эластичности:  , где B – коэффициент, показывающий угол наклона кривой спроса. Найдем объем спроса при заданной цене: 30 = 60 – 2 Qd, отсюда Qd = 15. Подставив значения в формулу, получим:  Ответ: Еd = 1. Задача 9 Постановка задачи: На рынке товара две группы потребителей, функции спроса которых записываются следующими формулами:  ,  . Определите, какой будет эластичность спроса по цене в точке, соответствующей Qd, равной 12. Технология решения задачи: Сначала определяется формула рыночного спроса на товар: Qd1 + Qd2 = 12 – Р + 12 – 3Р = 24 – 4Р. Находим цену товара при объеме спроса на рынке, равном 12 единиц: 12 = 24 – 4Р; Р = 3. Затем, применяя формулу точечной эластичности, находим коэффициент эластичности: 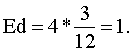, где B – коэффициент, показывающий угол наклона кривой спроса.  Ответ: 1. Задача 10 Постановка задачи: Функция спроса на товар имеет вид Qd = 50 – 2Р. Определите дуговую эластичность спроса по цене при снижении цены с 10 до 9 евро. Технология решения задачи: Определяем объем спроса при цене 10 евро: 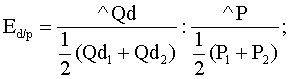 , а затем при цене 9 евро:  . После этого рассчитываем коэффициент эластичности:   Ответ: –0,61. Задачи на использование коэффициентов эластичности Задача 11 Постановка задачи: Ценовая эластичность спроса населения на товар составляет (–0,8), а эластичность спроса по доходу 1,3. Если цена на товар снизится на 2 %, а доход увеличится на 5 %, что произойдет со спросом на данный товар? Технология решения задачи: Объем спроса увеличится под воздействием снижения цены товара и увеличения дохода с учетом коэффициентов эластичности. Это рассчитывается следующим образом:  , где Inc – доход потребителя. Подставив значения, получим:  Ответ: Объем спроса увеличится на 8,1 %. Задача 12 Постановка задачи: Коэффициент перекрестной эластичности Еx/y = (–2). Цена товара Y равна 100 у. е. Определите спрос на товар Х, если цена товара Y увеличится на 10 %, а первоначальный спрос на товар Х равен 80 т. Технология решения задачи: Для решения задачи необходимо воспользоваться формулой расчета коэффициента перекрестной эластичности товара Х по формуле 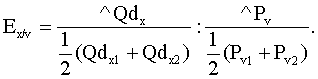 Следовательно, изменение объема спроса товара Х определяется путем перемножения коэффициента перекрестной эластичности на изменение цены товара У:  . Следовательно, объем спроса будет равен: Qdх = 80 * 0,95 = 76 т. Ответ: 76 т. Задача 13 Постановка задачи: При цене 10 у. е. объем спроса на товар А равен 1000 штук. Предприниматель решает изменить цену. Он определил, что при росте цены на 10 % эластичность товара становится равной (–1,2), при снижении цены на 10 % коэффициент эластичности равен (–0,8). На какой цене остановится предприниматель? Технология решения задачи: Для решения задачи надо определить, каким станет спрос при новой цене, а затем рассчитать выручку от продажи товара. При цене 10 у. е. предприниматель получает 10 000 у.е. Если цена снизится на 10 %, она станет равна 9 у. е., спрос на товар вырастет на  , т. е. станет 1000 * 1,08 = 1080 штук. Предприниматель получит от продажи этих товаров:  у. е. Выручка сократилась на 10 000 – 9720 = 280 у. е., следовательно, снижать цену нельзя. Если цена увеличится на 10 %, т. е. станет 11 у. е., спрос на товар упадет на 12 % (1,2 * 10 %), т. е. станет равен  . Продавая их по 11 у. е., предприниматель выручит 9680 у. е. Выручка снова сократилась, значит, увеличивать цену на 10 % тоже нельзя. Поэтому предпринимателю следует сохранить старую цену. Ответ: 10 у. е. | |||||||||||||||||||||||||