Подземная гидромеханика конртольная работа. Контрольная работа по дисциплине Подземная гидромеханика

• Название: Контрольная работа по дисциплине Подземная гидромеханика
• Дата: 14.10.2022
• Размер: 264 Kb.
• Имя файла: Подземная гидромеханика конртольная работа.doc
• Тип: Контрольная работа; #733001

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования
Пермский государственный технический университет

Горно-нефтяной факультет
Кафедра разработки нефтяных и газовых месторождений

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

«Подземная гидромеханика»


Выполнил: студент группы РНГМу-07-2 Ю.С. Турыгин

Проверил: ст.преподаватель И.Н. Пономарева

Пермь 2010

Раздел 1. Характеристики пористых сред. Модели грунта

1.3 Определить площадь поверхности зерен в объеме V фиктивного грунта пористостью m, при диаметре зерен d.

№ варианта	V, м3	m, %	d, мм
25	2,5	23	0,1

Решение:

Определим площадь поверхности зерен по формуле Оркина:

(m=23%=0,23 усл..ед.)

Ответ: .

Раздел 2. Основные понятия теории фильтрации. Законы фильтрации

2.3. Определить размеры зоны нелинейной фильтрации жидкости при движении нефти (вязкость μ=3 мПа·с, плотность ρ=770 кг/м3) в пласте (толщина h=22м; пористость m=0,19, проницаемость k=1,2 мкм2) к скважине, работающей с дебитом Q=55 м3/сут.
Решение:

Если , то закон фильтрации нелинейный. То есть зоной нелинейной фильтрации жидкости считается зона от r_кр.
Число Рейнольдса можно определить по формуле Щелкачева:





Таким образом зоной нелинейной фильтрации жидкости является зона до r=r_кр=0,016м.

Раздел.3. Простейшие фильтрационные потоки

3.3. Вычислить давление на контуре питания пласта, если расстояние от контура до возмущающей скважины r_к. Радиус скважины r_c, забойное давление Р_с. Известно, что давление на забое бездействующей скважины, находящейся на расстоянии r от возмущающей скважины, равно P. Приток жидкости к действующей скважине предполагается плоскорадиальным при линейном законе фильтрации.

№ варианта	rк, м	rс, см	Рс, МПа	r, м	Р, МПа
25	300	10	10	75	11

Решение:

Распределение давления в пласте подчиняется закону



Выразим отсюда давление на контуре питания: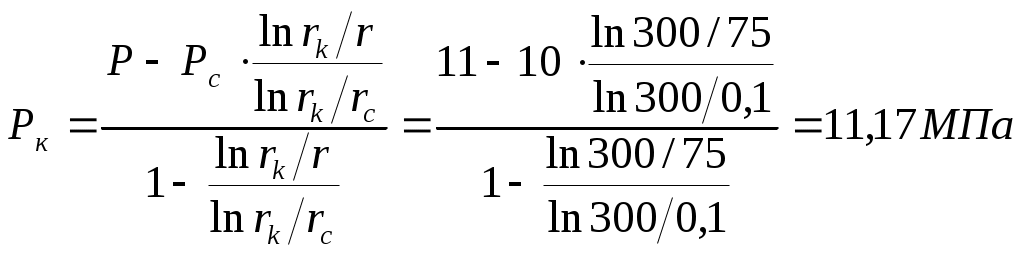

Раздел 4. Исследование скважин методом установившихся отборов

4.2. Произвести обработку результатов исследования скважины методом установившихся отборов.

Исходные данные:

Радиус контура питания r_к, радиус скважины r_c, эффективная нефтенасыщенная толщина пласта h, динамическая вязкость нефти μ.

№ варианта	rк, М	rс, СМ	h, М	μ,мПа-с	1 режим		2 режим		3 режим		4 режим
					Q, м3/сут	ΔР, МПа	Q, м3/сут	ΔР, МПа	Q, м3/сут	ΔР, МПа	Q, м3/сут	ΔР, МПа
25	350	10	16	4	48	6,559	53	7,971	57	9,2	59	9,847

Решение:

Строим индикаторную диаграмму в координатах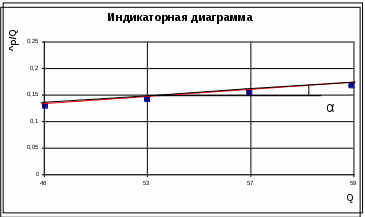


А










Обработка нелинейной индикаторной диаграммы выполняется в соответствии с двухчленной формулой притока:



А=0,137 МПа*сут/м3

В=tgα=tg 5°=0.087

Прямая линия отсекает на оси ординат отрезок А:



Из которой проницаемость:



Проводимость:



Гидропроводность:



Ответ: проницаемость

проводимость

гидропроводность


Раздел 5. Линейная фильтрация газа.

5.2. Построить кривую распределения давления вокруг скважины в случае плоскорадиального движения газа по линейному закону фильтрации при следующих исходных данных:

№ варианта	h, м	k, мкм2	μ, мПа·с	rс, см	rк, м	Рс, МПа	Qат, м3/сут
25	15	0,23	1,2	10	350	19	8800

Решение:

Найдем для заданного расхода газа Р_к: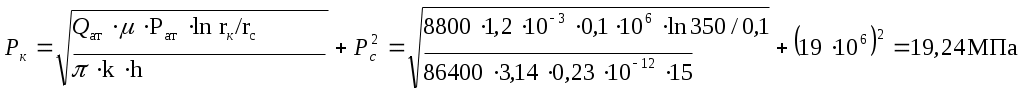



Составим таблицу распределения давления в зависимости от расстояния от скважины:

Расстояние от скважины,м.	Давление, МПа
150	19,21
200	19,22
250	19,23
300	19,24
350	19,25

_{Построим график распределения давления вокруг скважины:}



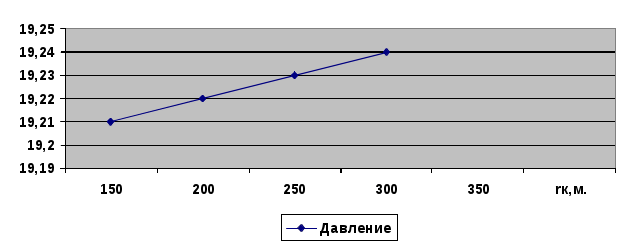Раздел 6. Установившееся движение газированной жидкости.

Задача 6.2. Найти фазовые проницаемости для нефти и газа, сумму относительных проницаемостей, а также отношение скоростей движения жидкости и газа, зная, что насыщенность жидкости порового пространства σ=65 %., абсолютная проницаемость горной породы k=0,4 мкм², вязкость μ_ж=7мПа·с, вязкость газа μ_г=0,3мПа·с. Пористая среда представлена несцементированным песком.

Решение:

По графикам (приложение, рис.7) при σ=65 % k_н =0,23; k_г =0,17

Фазовая проницаемость:

k_н =0,23х0,4=0,092 мкм²

k_г =0,17х0,4=0,068 мкм²

Относительная проницаемость:

k_н= k_н/ k=0,23/0,4=0,575мкм²

k_г= k_г/ k_г=0,17/0,4=0,425мкм²

Раздел 7. Движение жидкости к гидродинамически несовершенным скважинам

7.2. Определить дебит скважины, гидродинамически несовершенной по характеру вскрытия пласта. Радиус скважины r_с=10 см, радиус контура питания пласта r_к=400м., коэффициент проницаемости k=0,9 мкм², толщина пласта h=13м., вязкость нефти μ=10,5 мПа·с, пластовое давление Р_к=21МПа, забойное давление Р_с=16 МПа. Эксплуатационная колонна и пласт вскрыты пулевым перфоратором с диаметром пуль d₀=20мм, и глубиной проникновения пуль в породу на =4см. Плотность перфорации n=19отв/м. Определить дебит скважины без учета её гидродинамического несовершенства.

Решение:

Гидродинамическое несовершенство скважины по степени вскрытия пласта учитывается коэффициентом С₁, по характеру вскрытия – С₂.

В нашем случае скважина несовершенна по характеру вскрытия



Коэффициент С₂ можно определить по графикам В.И. Щурова:

,

где - глубина проникновения пуль в породу.

№ кривой на рис.9 или 10 для определения коэффициента С₂ выбирается в соответствии с параметром α по табл.10 (учебно-методического пособия).

,

где d – диаметр пуль (перфорационных отверстий).
Следовательно, номер кривой – 7.



С₂=1,8.



Дебит скважины: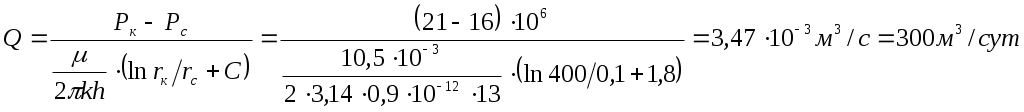



Дебит скважины без учета гидродинамического несовершенства: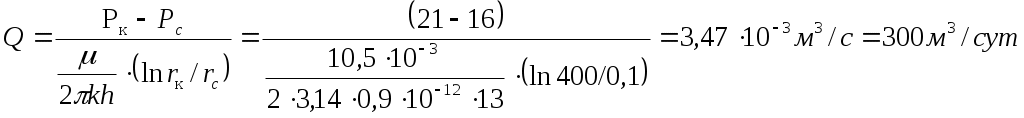





Раздел 8. Гидродинамические исследования скважин при неустановившихся режимах.

8.1. В результате исследования добывающей скважины на неустановившихся режимах получены значения забойного давления в различные моменты времени после остановки скважины. Определить фильтрационные параметры пласта, если известно, что в пласте толщиной h фильтруется нефть вязкостью . До остановки скважина работала с установившимся дебитом Q.

№ варианта	h, м	μ, мПа·с	Q, м3/сут
25	5	3,9	90

25 вариант
t, мин	Р, МПа	^Р, МПа	Ln,t
0	10,173	0
15	10,442	0,269	2,7
30	10,526	0,353	3,4
45	10,565	0,392	3,8
60	10,619	0,446	4,1
90	10,703	0,530	4,5
120	10,792	0,619	4,8
150	10,890	0,717	5
165	10,963	0,790	5,1
1230	12,665	1,862	7,1
2880	14,078	3,905	8
4490	14,550	4,377	8,4
6000	14,670	4,497	8,7
6940	14,685	4,512	8,8
8640	14,750	4,577	9,1
10174	14,767	4,594	9,2

Решение:

Строится график в координатах ΔР – ln t (ΔР = Рt – Р0).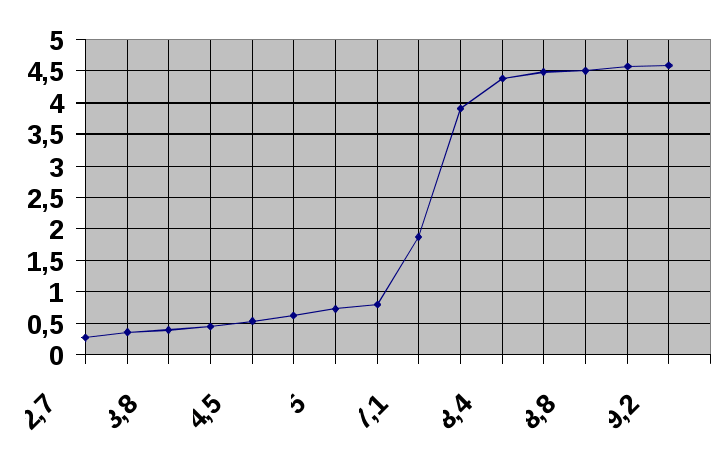



В качестве прямолинейного принимаем участок (точки 11 – 15).

Уклон выделенного прямолинейного участка



Гидропроводность пласта



Проницаемость пласта



Раздел 9. Неустановившееся движение жидкости при работе скважин с переменным дебитом

9.1. Определить величину пластового давления в точке А (x₀, y₀), расположенной в бесконечном изотропном пласте, в котором работают две скважины (первая – добывающая, вторая – нагнетательная). Скважины работают с переменным дебитом. Толщина пласта h, проницаемость k, пористость m, коэффициенты объемного сжатия жидкости β_ж и горной породы β_п, вязкость жидкости μ = 1 мПас, начальное пластовое давление Р_{пл 0}.

№ варианта	q1, м3/сут			интервалы времени, сут			q2, м3/сут		интервалы времени, сут		h, м	k, мкм2
25	240	160	290	300	400	300	40	90	450	550	27	0,47

№ варианта	m, %	βп, 10-10 1/Па	βж, 10-10 1/Па	Р0, МПа	Координаты скважин, м
					x0	y0	x1	y1	x2	y2
25	22	1	7,8	17	600	800	800	1200	0	0

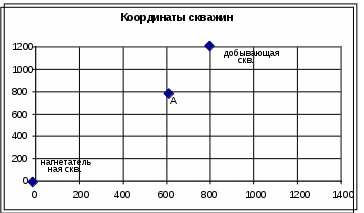Решение:

Находим коэффициент пьезопроводности:



<sub>Находим расстояние между добывающей скважиной и точкой А:



Находим расстояние между нагнетательной скважиной и точкой А:</sub>



Находим изменение давления, вызванное работой фиктивных добывающих скважин: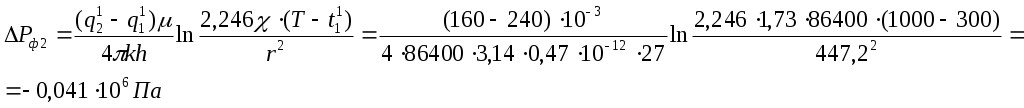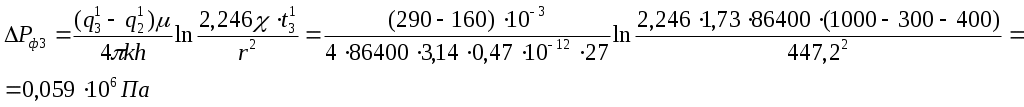









Суммарное изменение давления:



Находим изменение давления, вызванное работой фиктивных нагнетательных скважин: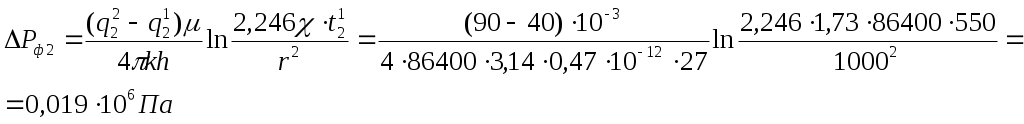







Суммарное изменение давления:



Пластовое давление в точке А: