статистика артем. 1. Понятие об абсолютных и относительных величинах, их значение. Виды относительных величин
 Скачать 41.86 Kb. Скачать 41.86 Kb.
|
|
План. Введение 1.Понятие об абсолютных и относительных величинах, их значение. Виды относительных величин. 2.Статистические индексы. 3.Задача 1. 4.Задача 2. Список литературы Введение 1. Понятие об абсолютных и относительных величинах, их значение. Виды относительных величин. Статистический показатель — количественная характеристика социально-экономических явлений и процессов в условиях качественной определенности. Различают показатель-категорию и конкретный статистический показатель: Показатель категория определяет содержание статистического показателя, то есть не численное значение определенного показателя, а его элементы: например коэффициент рождаемости, смертности, национального богатства. Конкретный статистический показатель — это цифровая характеристика изучаемого явления или процесса. Например: численность населения России на данный момент составляет 145 млн.человек. По форме различают статистические показатели: Абсолютные Относительные Средние По охвату единиц различают индивидуальные и сводные показатели. Индивидуальные показатели — характеризуют отдельный объект или отдельную единицу совокупности (прибыль фирмы, размер вклада отдельного человека). Сводные показатели — характеризуют часть совокупности или в всю статистическую совокупность в целом. Их можно получить как объемные и расчетные. Объемные показатели получают путем сложения значений признака отдельных единиц совокупности. Полученная величина называется объемом признака. Расчетные показатели вычисляются по различным формулам и используются при анализе социально-экономических явлений. Статистические показатели по временному фактору делятся на: Моментные показатели — отражают состояние или уровень явления на определенный момент времени. Например, число вкладов в Сбербанке на конец какого-либо периода. Интервальные показатели — характеризуют итоговый результат за период (день, неделя, месяц, квартал, год) в целом. Например, объем произведенной продукции за год. Статистические показатели связаны между собой. Поэтому, чтообы составить целостное представление об изучаемом явлении или процессе, необходимо рассматривать систему показателей. Абсолютная величина Статистика измеряет и выражает явления общественной жизни с помощью количественных категорий — статистических величин. Результаты статистического наблюдения получают прежде всего в форме абсолютных величин, которые служат основой для расчета и анализа статистических показателей на следующих этапах статистического исследования. Абсолютная величина — объем или размер изучаемого события или явления, процесса, выраженного в соответствующих единицах измерения в конкретных условиях места и времени. Виды абсолютных величин: Индивидуальная абсолютная величина — характеризует единицу совокупности Суммарная абсолютная величина — характеризует группу единиц или всю совокупность Результатом статистического наблюдения являются показатели, которые характеризуют абсолютные размеры или свойства изучаемого явления у каждой единицы наблюдения. Они называются индивидуальными абсолютными показателями. Если показатели характеризуют всю совокупность в целом, они называются обобщающими абсолютными показателями. Статистические показатели в форме абсолютных величин всегда имеют единицы измерения: натуральные или стоимостные. Формы учета абсолютных величин: Натуральный — физические единицы (штук, человек) Условно-натуральный — применяется при подсчете итогов по продукции одинакового потребительского качества но широкого ассортимента. Перевод в условное измерение осуществляется с помощью коэффициента пересчета: Кпересчета=фактическое потребительское качество / эталон (заранее заданное качество) Стоимостной учет — денежные единицы Натуральные единицы измерения бывают простыми, составными и условными. Простые натуральные единицы измерения — это тонны, километры, штуки, литры, мили, дюймы и т. д. В простых натуральных единицах также измеряется объем статистической совокупности, т. е. число составляющих ее единиц, или объем отдельной ее части. Составные натуральные единицы измерения имеют расчетные показатели, получаемые как произведение двух или нескольких показателей, имеющих простые единицы измерения. Например, учет затрат труда на предприятиях выражается в отработанных человеко-днях (число работников предприятия умножается на количество отработанных за период дней) или человеко-часах (число работников предприятия умножается на среднюю продолжительность одного рабочего дня и на количество рабочих дней в периоде); грузооборот транспорта выражается в тонно-километрах (масса перевезенного груза умножается на расстояние перевозки) и т. д. Условно-натуральные единицы измерения широко используют в анализе производственной деятельности, когда требуется найти итоговое значение однотипных показателей, которые напрямую несопоставимы, но характеризуют одни и те же свойства объекта. Натуральные единицы пересчитываются в условно-натуральные путем выражения разновидностей явления в единицах какого-либо эталона. Например: различные виды органического топлива переводятся в условное топливо с теплотой сгорания 29,3 МДж/ кг мыло разных сортов — в условное мыло с 40%-ным содержанием жирных кислот консервы различного объема — в условные консервные банки объемом 353,4 см3, для подсчета общего объема работы транспорта складывают тонно-километры перевезенных грузов и пассажиро-километры, произведенные пассажирским транспортом, условно приравнивая при этом перевозку одного пассажира к перевозке одной тонны груза и т. д. Перевод в условные единицы осуществляется с помощью специальных коэффициентов. Например, если имеется 200 т мыла с содержанием жирных кислот 40% и 100 т с содержанием жирных кислот 60%, то в пересчете на 40%-ное, получим общий объем 350 т условного мыла (коэффициент пересчета определяется как отношение 60 : 40 = 1,5 и, следовательно, 100 т · 1,5 = 150 т условного мыла). Пример 1 Найти условно-натуральную величину: Допустим мы производим тетради: по 12 листов — 1000 шт; по 24 листа — 200 шт; по 48 листов — 50 шт; по 96 листов — 100 шт. Решение: Задаем эталон — 12 листов. Считаем коэффициент пересчета: 12/12=1 24/12=2 48/12=4 96/12=8 Ответ: Условно натуральная величина =1000*1 + 200*2 + 50*4 + 100*8 = 2400 тетрадей по 12 листов В условиях рыночной экономики наибольшее значение и применение имеют стоимостные единицы измерения: рубли, доллары, евро, условные денежные единицы и др. Для оценки социально-экономических явлений и процессов используются показатели в текущих или фактически действующих ценах или в сопоставимых ценах. Сама по себе абсолютная величина не дает полного представления об изучаемом явлении, не показывает его структуру, соотношение между отдельными частями, развитие во времени. В ней не выявлены соотношения с другими абсолютными величинами. Поэтому статистика, не ограничиваясь абсолютными величинами, широко использует общенаучные методы сравнения, обобщения. Абсолютные величины имеют большое научное и практическое значение. Они характеризуют наличие тех или иных ресурсов и являются основой разнообразных относительных показателей. Относительные величины Наряду с абсолютными величинами в экономическом анализе и экономической статистике используются также различные относительные величины. Относительные величины представляют собой различные коэффициенты или проценты. Относительные статистические величины — это показатели, которые дают числовую меру соотношения двух сопоставляемых между собой величин. Основное условие правильного расчета относительных величин — сопоставимость сравниваемых величин и наличие реальных связей между изучаемыми явлениями. Относительная величина = сравниваемая величина / базис Величина, находящаяся в числителе соотношения, называется текущей или сравниваемой. Величина, находящаяся в знаменателе соотношения, называется основанием или базой сравнения. По способу получения относительные величины — это всегда всегда величины производные (вторичные). Они могут быть выражены: в коэффициентах, если база сравнения принимается за единицу (АбсВеличина / Базис) * 1 в процентах, если база сравнения принимается за 100 (АбсВеличина / Базис) * 100 в промилле, если база сравнения принимается за 1000 (АбсВеличина / Базис) * 1000 Например показатель рождаемости в форме относительной величины, исчисляемый в промилле показывает число родившихся за год в расчете на 1000 человек. в продецимилле, если база сравнения принимается за 10000 (АбсВеличина / Базис) * 10000 Различают следующие виды относительных статистических величин: Относительная величина динамики Относительная величина планового задания Относительная величина выполнения плана Относительная величина структуры Относительная величина координации Относительная величина интенсивности Относительная величина сравнения Относительная величина координации Относительная величина координации (показатель координации) — представляет собой соотношение частей совокупности между собой. При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо иной точки зрения. ОВК = показатель характеризующий часть совокупности / показатель характеризующий часть совокупности, выбранную за базис сравнения Относительная величина координации показывает, во сколько раз одна часть совокупности больше или меньше другой, принятой за базу сравнения, или сколько процентов от нее составляет, или сколько единиц одной части целого приходится на 1, 10, 100, 1000,..., единиц другой (базисной) части. Например в 1999 г. в России насчитывалось 68,6 млн.мужчин и 77,7 млн.женщин, следовательно, на 1000 мужчин приходилось (77,7/68,6)*1000=1133 женщины. Аналогично можно рассчитать сколько на 10 (100) инженеров приходится техников; число мальчиков, приходящихся на 100 девочек среди новорожденных и др. Пример: на предприятии работают 100 менеджеров 20 курьеров и 10 руководителей. Решение: ОВК = (100 / 20)*100% = 500%. Менеджеров в 5 раз больше чем курьеров. тоже самое с помощью ОВС (пример 5): ( 77%/15% ) * 100% = 500% Относительная величина структуры Относительная величина структуры (показатель структуры)- характеризует удельный вес части совокупности в ее общем объеме. Относительную величину структуры часто называют "удельный вес" или "доля". ОВС = показатель, характеризующий часть совокупности / показатель по всей совокупности в целом Пример: на предприятии работают 100 менеджеров 20 курьеров и 10 руководителей. Всего 130 чел. Доля курьеров =( 20/130 ) * 100% = 15% Удельный вес менеджеров = (100 / 130) * 100% = 77% ОВС руководителей = 8% Сумма всех ОВС должна быть равна 100% или единице. Относительная величина сравнения Относительная величина сравнения (показатель сравнения) — характеризует соотношение между разными совокупностями по одноименным показателям. Пример 8: Объем выданных кредитов частным лицам на 1 февраля 2008 г. Сбербанком России составил 520189 млн.руб, по Внешторгбанку — 10915 млн.руб. Решение: ОВС = 520189 / 10915 = 47,7 Таким образом, объем выданных кредитов частным лицам Сбербанком России на 1 февраля 2006 г. был выше в 47,7 раза, чем аналогичный показатель Внешторгбанка. 2.Статистические индексы. Статистический индекс — это относительная величина сравнения сложных совокупностей и отдельных их единиц. При этом под сложной понимается такая статистическая совокупность, отдельные элементы которой непосредственно не подлежат суммированию. Индекс - это результат сравнения двух одноименных показателей, при исчислении которого следует различать числитель индексного отношения (сравниваемый или отчетный уровень) и знаменатель индексного отношения (базисный уровень, с которым производится сравнение). Выбор базы зависит от цели исследования. Если изучается динамика, то за базисную величину может быть взят размер показателя в периоде, предшествующем отчетному. Если необходимо осуществить территориальное сравнение, то за базу можно принять данные другой территории. За базу сравнения могут приниматься плановые показатели, если необходимо использовать индексы как показатели выполнения плана. Индексы формируют важнейшие экономические показатели национальной экономики и ее отдельных отраслей. Индексные показатели позволяют осуществить анализ результатов деятельности предприятий и организаций, выпускающих самую разнообразную продукцию или занимающихся различными видами деятельности. С помощью индексов можно проследить роль отдельных факторов при формировании важнейших экономических показателей, выявить основные резервы производства. Индексы широко используются в сопоставлении международных экономических показателей при определении уровня жизни, деловой активности, ценовой политики и т.д. Существует два подхода в интерпретации возможностей индексных показателей: обобщающий (синтетический) и аналитический, которые в свою очередь определяются разными задачами. Суть обобщающего подхода - в трактовке индекса как показателя среднего изменения уровня исследуемого явления. В этом случае основной задачей, решаемой с помощью индексных показателей, будет характеристика общего изменения многофакторного экономического показателя. Аналитический подход рассматривает индекс как показатель изменения уровня результативной величины, на которую оказывает влияние величина, изучаемая с помощью индекса. Отсюда и иная задача, которая решается с помощью индексных показателей: выделить влияние одного из факторов в изменении многофакторного показателя. От содержания изучаемых показателей, методологии расчета первичных показателей, целей и задач исследования зависят и способы построения индексов. По степени охвата элементов явления индексы делят на индивидуальные и общие (сводные). Индивидуальные индексы (i) - это индексы, которые характеризуют изменение только одного элемента совокупности. Показатели, характеризующие изменение более или менее однородных объектов, входящих в состав сложного явления, называются индивидуальными индексами – ix. p – цена q – количество t – время T – численность f – з/п F – фонд з/п S – посевная площадь y – урожайность z – себестоимость Индекс получает название по названию индексируемой величины. В большинстве случаев в числителе стоит текущий уровень, а в знаменателе – базисный уровень. Исключением является индекс покупательной способности рубля. Индексы измеряются либо в виде процентов (%), либо в виде коэффициентов. Общий (сводный) индекс (I) характеризует изменение по всей совокупности элементов сложного явления. Если индексы охватывают только часть явления, то их называют групповыми. В зависимости от способа изучения общие индексы могут быть построены или как агрегатные (от лат. аggrega - присоединяю) индексы, или как средние взвешенные индексы (средние из индивидуальных). Способ построения - агрегатных индексов заключается в том, что при помощи так называемых соизмерителей можно выразить итоговые величины сложной совокупности в отчетном и базисном периодах, а затем первую сопоставить со второй. В статистике имеют большое значение индексы переменного и фиксированного состава, которые используются при анализе динамики средних показателей. Индексом переменного состава называют отношение двух средних уровней. Индекс фиксированного состава есть средний из индивидуальных индексов. Он рассчитывается как отношение двух стандартизованных средних, где влияние изменения структурного фактора устранено, поэтому данный индекс называют еще индексом постоянного состава. В зависимости от характера и содержания индексируемых величин различают индексы количественных (объемных) показателей и http://hi-edu.ru/e-books/xbook096/01/predmetnyi.htm - i796индексы качественных показателей. Индексы количественных показателей К индексам количественных (объемных) показателей относятся такие индексы, как индексы физического объема производства продукции, затрат на выпуск продукции, стоимости продукции, а также индексы показателей, размеры которых определяются абсолютными величинами. Используются различные виды индексов количественных показателей. Индекс физического объема продукции (ФОП) отражает изменение выпуска продукции. Индивидуальный индекс ФОП отражает изменение выпуска продукции одного вида и определяется по формуле где q1 и q0 - количество продукции данного вида в натуральном выражении в текущем и базисном периодах. Агрегатный индекс ФОП (предложен Э. Ласпейресом) отражает изменение выпуска всей совокупности продукции, где индексируемой величиной является количество продукции q, а соизмерителем - цена р: где q1 и q0 - количество выработанных единиц отдельных видов продукции соответственно в отчетном и базисном периодах; p0 - цена единицы продукции (отдельного вида) в базисном периоде. При вычислении индекса ФОП в качестве соизмерителей может выступать также себестоимость продукции или трудоемкость. Средние взвешенные индексы ФОП используются в том случае, если известны индивидуальные индексы объема по отдельным видам продукции и стоимость отдельных видов продукции (или затраты) в базисном или отчетном периоде. Средний взвешенный арифметический индекс ФОП определяется по формуле где iq - индивидуальный индекс по каждому виду продукции; q0 p0 - стоимость продукции каждого вида в базисном периоде. Средний взвешенный гармонический индекс ФОП 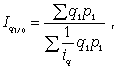 (4) (4)где q1 p1 - стоимость продукции каждого вида в текущем периоде. Аналогично рассчитывается индекс затрат на выпуск продукции (ЗВП), который отражает изменение затрат на производство и может быть как индивидуальным, так и агрегатным. Индивидуальный индекс ЗВП отражает изменение затрат на производство одного вида и определяется по формуле где z1 и z0 - себестоимость единицы продукции искомого вида в текущем и базисном периодах; q1 z1 и q0 z0 - суммы затрат на выпуск продукции искомого вида в текущем и базисном периодах. Агрегатный индекс ЗВП характеризует изменение общей суммы затрат на выпуск продукции за счет изменения количества выработанной продукции и ее себестоимости и определяется по формуле где q1 z1 и q0 z0 - затраты на выпуск продукции каждого вида соответственно в отчетном и базисном периодах. Рассмотрим построение индекса стоимости продукции (СП), который может определяться и как индивидуальный, и как агрегатный. Индивидуальный индекс СП характеризует изменение стоимости продукции данного вида и имеет вид: где p1 и p0 - цена единицы продукции данного вида в текущем и базисном периодах; q1 p1 и q0 p0 - стоимость продукции данного вида в текущем и базисном периодах. Агрегатный индекс СП (товарооборота) характеризует изменение общей стоимости продукции за счет изменения количества продукции и цен и определяется по формуле Индексы качественных показателей. Факторный анализ Качественные показатели определяют уровень исследуемого итогового показателя и определяются путем соотношения итогового показателя и определенного количественного показателя (например, средняя заработная плата определяется путем соотношения фонда заработной платы и количества работников). К индексам качественных показателей относятся индексы цен, себестоимости, средней заработной платы, производительности труда. Самым распространенным индексом в этой группе является индекс цен. Индивидуальный индекс цен характеризует изменение цен по одному виду продукции и определяется по формуле где p1 и p0 - цена за единицу продукции в текущем и базисном периодах. Соответственно определяются индексы себестоимости и затрат рабочего времени по каждому виду продукции. Агрегатный индекс цен определяет среднее изменение цены р по совокупности определенных видов продукции q. Для характеристики среднего изменения цен на потребитель-ские товары используют индекс цен, предложенный Э. Ласпейресом (индекс Ласпейреса):  (10) (10)где q0 - потребительская корзина (базовый период); p0 и p1 - соответственно цены базисного и отчетного периодов. Если количество набора продуктов принимается на уровне отчетного периода (q1 ), то в этом случае индекс цен именуется индексом Пааше: Если известны индивидуальные индексы цен по отдельным видам продукции и стоимость отдельных видов продукции, то применяются средние взвешенные индексы цен (средний взвешенный арифметический и средний взвешенный гармонический индексы цен). Формула среднего взвешенного арифметического индекса цен 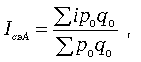 (12) (12)где i - индивидуальный индекс по каждому виду продукции; p0 q0 - стоимость продукции каждого вида в базисном периоде. Формула среднего взвешенного гармонического индекса цен 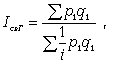 (13) (13)где p1 q1 - стоимость продукции каждого вида в текущем периоде. В статистической практике очень широко используется агрегатный территориальный индекс цен, который может быть рассчитан по следующей формуле: где pA pB - цена за единицу продукции каждого вида соответственно на территории А и В; qA - количество выработанной или реализованной продукции каждого вида по территории А (в натуральном выражении). Из формулы видно, что в данном индексе в качестве фиксированного показателя (веса) принят объем продукции территории А. При расчете данного индекса в качестве веса можно принять также объем продукции территории В или суммарный объем продукции двух территорий. Возможны два способа расчета индексов: цепной и базисный. Цепные индексы получают путем сопоставления текущих уровней с предшествующим, при этом база сравнения постоянно меняется. Базисные индексы получают путем сопоставления с тем уровнем периода, который был принят за базу сравнения. В качестве примера можно привести цепные и базисные индексы цен. Цепные индивидуальные индексы цен имеют следующий ряд расчета: Базисные индивидуальные индексы цен: Следует помнить, что произведение цепных индивидуальных индексов цен равно последнему базисному индексу: Цепные агрегатные индексы цен: Базисные агрегатные индексы цен: Между индексами существует также взаимосвязь и взаимозависимость, как и между самими экономическими явлениями, что позволяет проводить факторный анализ. Благодаря индексному методу можно рассматривать все факторы независимо друг от друга, что дает возможность определить размер абсолютного изменения сложного явления за счет каждого фактора в отдельности. Предположим, что результативный признак зависит от трех факторов и более. В этом случае результативный индекс примет вид Изменение результативного индекса за счет каждого фактора может быть выражено следующим образом: Для выявления роли каждого фактора в отдельности индекс сложного показателя разлагают на частные (факторные) индексы, которые характеризуют роль каждого фактора. При этом используют два метода: 1. метод обособленного изучения факторов; 2. последовательно-цепной метод. При первом методе сложный показатель берется с учетом изменения лишь того фактора, который взят в качестве исследуемого, все остальные остаются неизменными на уровне базисного периода. Последовательно-цепной метод предполагает использование системы взаимосвязанных индексов, которая требует определенного расположения факторов. Как правило, на первом месте в цепи располагают качественный фактор. При определении влияния первого фактора все остальные сохраняются в числителе и знаменателе на уровне базисного периода, при определении второго факторного индекса первый фактор сохраняется на уровне базисного периода, а третий и все последующие - на уровне отчетного периода, при определении третьего факторного индекса первый и второй факторы сохраняются на уровне базисного периода, четвертый и все остальные - на уровне отчетного периода и т.д. |
