контрольная ПГРЛ 61. Контрольная работа по дисциплине Промысловая гидроакустика и рыболокация Вариант 61 Выполнил студент Шифр
 Скачать 181.33 Kb. Скачать 181.33 Kb.
|
|
Федеральное агентство по рыболовству Калининградский государственный технический университет Балтийская государственная академия рыбопромыслового флота КОНТРОЛЬНАЯ РАБОТА по дисциплине «Промысловая гидроакустика и рыболокация» Вариант 61 Выполнил студент _____________ Шифр Проверил к.т.н. Ермаков С.В. Калининград 2022 Задача 7:Условие задачи: Найти, чему равно волновое сопротивление среды для плоской волны, имеющей частоту 1,5 кГц, если при измерениях оказалось, что эффективное значение звукового давления равно 1,5 Па, а амплитуда смещения частиц была 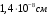 . .Теоретическое введение Скорость, с которой происходит передача колебательного движения от частицы к частице среды или возмущенного состояния от точки к точке среды, называется скоростью распространения звуковой волны или скоростью звука. Очевидно, что чем частица тяжелее (выше ее плотность) и чем упругие связи между частицами слабее (т.е. более сжимаема среда), тем медленнее передаются колебания и тем меньше скорость звука. Таким образом, последняя зависит только от двух параметров среды: ее плотности и упругости (сжимаемости): 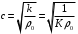 где 0 статическая (равновесная) плотность среды; модуль объемной упругости среды; K коэффициент сжимаемости среды. Решение: Волновое сопротивление определяется из формулы: 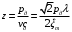 Длина волны звука определяется из формулы: 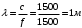 Получим: 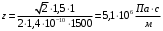 Ответ: 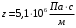 Задача 38:Условие задачи: Вычислить, каким будет коэффициент отражения по энергии от песчаного морского дна при нормальном падении волны, если скорость звука в песчаном грунте на 20% больше скорости звука в воде, а плотность песчаного грунта в 2 раза больше плотности воды. Теоретическое введение: Пусть на гладкую протяженную границу раздела сред падает плоская звуковая волна i, при этом образуется отраженная звуковая волна r и преломленная волна t. Проведем нормаль к границе раздела сред и обозначим угол падения Θi , угол отражения Θr и угол преломления Θ t . 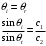 Декарт доказал, что рассматриваемые три луча как и три угла лежат в одной плоскости, и что угол отражения равен углу падения, а отношение синусов углов падения и преломления равно отношению скоростей звука в граничащих средах. Так формулируются законы Декарта. 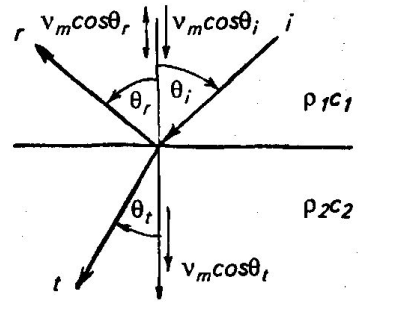 Рисунок 1 - Углы падения, отражения и преломления Коэффициенты отражения и преломления устанавливают связь между амплитудами и интенсивностями отраженной, преломленной и падающей на границу раздела сред волн. Коэффициентом отражения по звуковому давлению называется отношение амплитуды или эффективного значения звукового давления отраженной волны к амплитуде или эффективному значению звукового давления падающей волны: 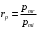 В свою очередь, коэффициентом преломления по звуковому давлению называется отношение амплитуды или эффективного значения звукового давления преломленной волны к амплитуде или эффективному значению звукового давления падающей волны: 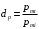 Аналогичным образом определяются коэффициенты отражения и преломления по колебательной скорости и интенсивности: 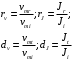 Решение: При нормальном падении волны на границу раздела сред, коэффициент отражения по энергии определяется по формуле:  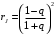 В свою очередь, нормированное волновое сопротивление, с учётом исходных данных, будет определяться по формуле: 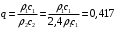 В итоге, получим: 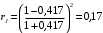 Ответ: 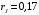 Задача 69Условие задачи: Чему была равна акустическая мощность антенны эхолота, работающего на частоте 150кГц, если ширина диаграммы направленности антенны на нулевом уровне равна 30о и на расстоянии 100 м от днища судна создаётся эффективное звуковое давление, равна 1 Па. Теоретическое введение: Децибел – логарифмическая относительная единица, применяемая для сравнения уровней одноименных величин – в основном двух звуковых давлений или двух интенсивностей: 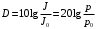 , ,где J,p – интенсивность и звуковое давление исследуемого сигнала, J0,p0 – интенсивность и звуковое давление, с которым сравнивают исследуемый сигнал. Акустическая мощность Pa – количество энергии, переносимое волной за единицу времени через всю волновую поверхность (через всю ее площадь Sв ). В свою очередь, интенсивность звуковой волны J – количество энергии, переносимое волной за единицу времени через единицу площади волновой поверхности, или, принимая во внимание данное выше определение, акустической мощности, интенсивность – это акустическая мощность, приходящаяся на единицу площади волновой поверхности: 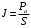 Решение: Интенсивность звука определяется из выражения: 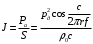 В итоге, получим: 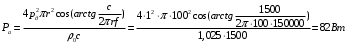 Ответ: 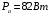 Задача 100:Условие задачи: Выяснить, до какого горизонта заглубится звуковой луч, излучённый под углом скольжения 15о с поверхности моря, если распределение звука по глубине подчинено зависимости 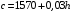 Теоретическое введение: Непостоянство скорости звука в морской воде существенного сказывается на характере распространения звуковых волн. Непрерывное изменение скорости звука от точки к точке в морской воде приводит к искривлению траектории звукового луча (к рефракции). Из-за того, что скорость звука и плотность морской воды изменяются от точки к точке, будет изменяться и волновое сопротивление воды по мере распространения волны, а это неизбежно вызовет рассеяние звуковой энергии – рефракционное рассеяние. Морская вода – среда неоднородная, включающая в себя воздушные пузырьки, зоо- и фитопланктон, твердые частички различного происхождения. На таких неоднородностях происходит рассеяние энергии распространяющейся звуковой волны, приводящее к ее постепенному затуханию, а также к возникновению объемной реверберации – послезвучания, фоном которого могут маскироваться полезные звуковые сигналы. Присутствие молекул солей в морской воде, наличие вязкости и теплопроводности (хоть и малых) приводит к поглощению звуковой волны и, следовательно, к ее затуханию. Существенное влияние на распространение звуковых волн в море оказывают его границы. Верхняя граница моря «вода-воздух» является почти идеально акустически мягкой и поэтому хорошо отражающей звуковые волны. Однако поверхность моря почти никогда не бывает спокойной, и поэтому зеркального отражения звуковых волн на ней практически не наблюдается. Звуковые волны, распространяющиеся вдоль поверхности моря, претерпевают рассеяние на неровностях верхней границы, в результате чего звуковая волна может постепенно затухать. Звуковые волны, рассеиваясь неровной поверхностью моря, порождают поверхностную реверберацию (послезвучание), фон которой также может оказывать маскирующее действие на полезные сигналы. Морское дно практически тоже никогда не бывает ровным (обладает микрорельефом), поэтому падающие на дно звуковые волны также рассеиваются во все стороны, порождая донную реверберацию, которая опять же может являться маскирующей полезные сигналы помехой. Характер изменения скорости звука по глубине моря соответствует в основном характеру распределения температуры воды по глубине, но возможны случаи, когда превалирующая роль в изменении скорости звука играет распределение солености или гидростатического давления. Вертикальное распределение скорости звука в общих чертах соответствует сезонным изменениям температуры и солености. Однако на эти закономерные временные изменения скорости звука с глубиной всегда в той или иной мере накладываются изменения случайного характера, приводящие к неустойчивому, случайному характеру распределения ее по глубине моря. Тем не менее, можно выделить некоторые типичные случаи вертикального распределения скорости звука. Постоянство скорости звука по глубине. В этом случае очевидно, что градиент скорости звука по всей глубине равен нулю, что характерно для мелководных районов средних широт зимой и осенью (температура и соленость по глубине выравниваются). Постоянство скорости звука из-за вертикальной циркуляции вод может наблюдаться в приповерхностном слое в глубоком море. Здесь после изотермического слоя обычно наблюдается увеличение скорости звука с глубиной. Линейное повышение скорости звука с глубиной. В этом случае градиент скорости звука постоянен с глубиной, а скорость звука определяется по простой формуле: 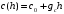  Рисунок 2 - Типичные случаи распределения скорости звукапо глубине моря Решение: Из анализа уравнения распределения скорости звука: 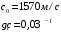 Из з. Снеллиуса: 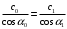 , где , где 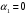 Получим: 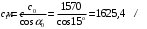 Заглубление звукового луча найдём из выражения: 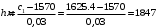 Ответ: 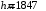 Задача 140: Условие задачи: Найти, какова будет погрешность счёта у цифрового индикатора эхолота, рассчитанного на скорость звука 1478 м/с, если частота тактовых импульсов у него равна 7390 Гц. Теоретическое введение: Согласно основной формуле эхометода расстояние до объекта определяется следующим образом: 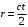 причем измерение временного запаздывания эхосигнала зависит от вида зондирующего сигнала – непрерывный он, или импульсный. В случае непрерывного сигнала применяется фазовый, частотный или корреляционный метод. Фазовый метод основан на пропорциональности измеряемой непосредственно разности фаз зондирующего сигнала и эхосигнала и временного запаздывания эхосигнала. Частотный метод заключается в излучении непрерывной модулированной по частоте звуковой волны. Закон модуляции чаще всего выбирается линейным Решение: Расстояние до объекта, выводимое на цифровой индикатор эхолота определяется из формулы: 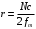 Откуда погрешность счёта получим: 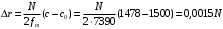 Ответ:погрешность будет равна 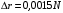 |
