|
|
Эконометрика, вариант 15. КР Эконометрика 15. Контрольная работа по дисциплине Статистика и эконометрика вариант 15 Исполнитель студентка курса Екатеринбург 2019
МИНИСТЕРСТВО НАУКИ И высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВО «Уральский государственный экономический университет»
Контрольная работа
по дисциплине: «Статистика и эконометрика »
вариант № 15
Исполнитель: студентка Ⅲ курса
Екатеринбург 2019
Регрессионный анализ

1. А)
|
У
|
Х1
|
Х2
|
Х3
|
У
|
|
0,991624
|
0,90649
|
0,932758
|
Х1
|
|
|
0,916853
|
0,922832
|
Х2
|
|
|
|
0,831775
|
Х3
|
|
|
|
|

Значение принятия нулевой гипотезы по константе меньше 0,05, поэтому она признаётся статистически значимой.
Если вероятность принятия нулевой гипотезы больше 0,05, то переменная признаётся статистически незначимой, то есть переменную Х2 следует исключить.
|
Коэффициенты
|
P-Значение
|
Y-пересечение
|
2049,08
|
0,36332
|
Переменная X 1
|
303,2149
|
3,08E-17
|
Переменная X 2
|
0,327437
|
0,036456
|
Рассчитанным значениям корреляции можно доверять.
Уравнение регрессии: Y = 2049,08 + 303,2149*X1 + 0,327437*X2.
Значение F = 5,04183E-31, F < 0,05, поэтому нулевая гипотеза отвергается. Следовательно, уравнение признаётся статистически значимым.
Регрессионная статистика
|
|
Множественный R
|
0,992682629
|
R-квадрат
|
0,985418802
|
Нормированный R-квадрат
|
0,984535093
|
Стандартная ошибка
|
4374,994664
|
Наблюдения
|
36
|
Дисперсионный анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
2
|
4,27E+10
|
21343549201
|
1115,094
|
5,04183E-31
|
Остаток
|
33
|
6,32E+08
|
19140578,31
|
|
|
Итого
|
35
|
4,33E+10
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
2049,07966
|
2222,894
|
0,92180728
|
0,36332
|
-2473,431707
|
6571,591
|
-2473,43
|
6571,591
|
Переменная X 1
|
303,214887
|
18,76386
|
16,1595116
|
3,08E-17
|
265,039518
|
341,3903
|
265,0395
|
341,3903
|
Переменная X 2
|
0,32743665
|
0,150168
|
2,18047485
|
0,036456
|
0,021918396
|
0,632955
|
0,021918
|
0,632955
|
Б) Данная регрессионная модель считается качественной, так как:
связь между переменными модели тесная (R 0,7);
в уравнении связи присутствуют лишь значимые факторы (все Р-значения меньше 0,05);
наблюдений для достоверных выводов достаточно (Значимость F меньше 0,05).
Вероятность незначимости (недостоверности) коэффициента корреляции мала: 5,04183E-31, значит, количество наблюдений достаточно.
В) Коэффициент детерминации R2 = 0,985418802 показывает, какая доля общей дисперсии объясняется уравнением регрессии:
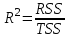 . .
Г) Стандартные ошибки коэффициентов регрессии:
|
Коэффициенты
|
Стандартная ошибка
|
Y-пересечение
|
2049,07966
|
2222,894
|
Переменная X 1
|
303,214887
|
18,76386
|
Переменная X 2
|
0,32743665
|
0,150168
|
Д) В результате выполнения регрессионного анализа в пакете Excel получены оценки а, b1,b2 и их доверительные интервалы:
|
Коэффициенты
|
Нижние 95%
|
Верхние 95%
|
Y-пересечение
|
2049,08
|
-2473,43
|
6571,591
|
Переменная X 1
|
303,2149
|
265,0395
|
341,3903
|
Переменная X 2
|
0,327437
|
0,021918
|
0,632955
|
Значит, -2473,43 < < 6571,591, 265,0395 < b1 < 341,3903 , 0,021918 < b2 < 0,632955.
Е) Нормированный R2 = 0,984535093 показывает, какая доля общей дисперсии объясняется включенными в регрессионную модель факторами (показателями, переменными).
Значения TSS, RSS и ESS выдались в качестве результатов выполнения регрессионного анализа в Excel в таблице «Дисперсионный анализ»:
RSS = 4,27E+10 – величина объяснённой дисперсии;
ESS = 6,32E+08 – величина остаточной дисперсии;
TSS = 4,33E+10 – величина общей дисперсии.
2.
№
|
Накладные расходы, руб. (У)
|
Объем работ, куб.м. (Х1)
|
Фонд заработной платы, руб. (Х2)
|
Расчётное значение спроса (Yрасчётное)
|
1
|
79761
|
218
|
26174
|
76720,252
|
2
|
124107
|
374
|
53546
|
132984,37
|
3
|
85270
|
242
|
28464
|
84747,2392
|
4
|
56397
|
139
|
24222
|
52127,1195
|
5
|
145995
|
420
|
59824
|
148987,903
|
6
|
103661
|
305
|
37174
|
106701,75
|
7
|
80047
|
217
|
28834
|
77288,0186
|
8
|
97654
|
281
|
38014
|
99699,6398
|
9
|
60585
|
160
|
20403
|
57244,1516
|
10
|
117824
|
312
|
40341
|
109861,246
|
11
|
132570
|
379
|
54202
|
134715,243
|
12
|
102816
|
285
|
46941
|
103835,526
|
13
|
193171
|
561
|
62277
|
192544,404
|
14
|
162639
|
455
|
60092
|
159688,177
|
15
|
127066
|
349
|
55156
|
125931,171
|
16
|
182923
|
508
|
54765
|
174014,311
|
17
|
101445
|
289
|
38557
|
102303,157
|
18
|
52198
|
130
|
23901
|
49293,0784
|
19
|
49938
|
139
|
18324
|
50195,8982
|
20
|
71518
|
201
|
22452
|
70346,8797
|
21
|
84552
|
232
|
30746
|
82462,3008
|
22
|
65016
|
187
|
20813
|
65565,2026
|
23
|
87197
|
238
|
29172
|
83766,2048
|
24
|
102038
|
315
|
39224
|
110405,144
|
25
|
146157
|
408
|
47225
|
141223,95
|
26
|
68673
|
206
|
24905
|
72666,1562
|
27
|
121496
|
360
|
41073
|
124655,245
|
28
|
69200
|
195
|
26462
|
69840,6113
|
29
|
99268
|
287
|
38714
|
101748,135
|
30
|
83586
|
247
|
25425
|
85268,2337
|
31
|
94654
|
238
|
35580
|
85864,4189
|
32
|
68479
|
210
|
25021
|
73916,9984
|
33
|
90667
|
258
|
28711
|
89679,5543
|
34
|
64674
|
192
|
24476
|
68280,6775
|
35
|
102939
|
321
|
30938
|
109511,294
|
36
|
87036
|
252
|
32599
|
89133,3386
|
Yрасчётное = b0 + b1х1+ b2х2
b2
|
b1
|
b0
|
0,32743665
|
303,21489
|
2049,08
|
0,150167588
|
18,763865
|
2222,894
|
0,985418802
|
4374,9947
|
#Н/Д
|
1115,09427
|
33
|
#Н/Д
|
42687098403
|
631639084
|
#Н/Д
|
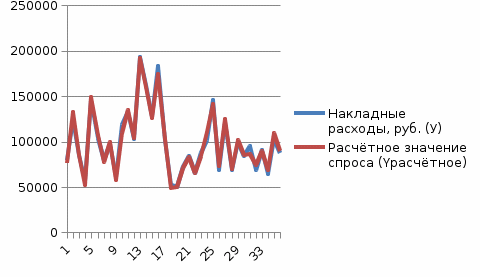
Построенная множественная линейная регрессия хорошо описывает исходные данные, ей можно пользоваться для прогнозирования Урасчётного. |
|
|
 Скачать 46.24 Kb.
Скачать 46.24 Kb.

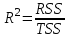 .
.
