Статистика. Контрольная работа по дисциплине Статистика Вариант 5 Дружинина Ксения Владимировна студент 2 курса
 Скачать 145.84 Kb. Скачать 145.84 Kb.
|
|
МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «СЕВЕРНЫЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ» Министерства здравоохранения Российской Федерации Кафедра экономики и управления Контрольная работа по дисциплине Статистика Вариант №5 Выполнил: Дружинина Ксения Владимировна студент 2 курса факультета экономики и управления направление «Менеджмент» подпись_______________________________________________ шифр: 181133001 номер зачетной книжки/студенческого билета Руководитель: Микитюк В.А., доцент подпись________________ оценка (отметка о зачете)__________ Архангельск, 2020 Содержание. Теоретический вопрос №1. Статистическая совокупность и статистический показатель, их роль и значение в экономико-статистических явлениях. Теоретический вопрос № 2. Корреляционно-регрессионный анализ статистической связи социально-экономических явлений. Задача №1 по теме «Статистическая сводка и группировка статистических данных». Задача №2 по теме «Относительные величины». Задача №3 по теме «Средние величины и показатели вариации». Задача №4 по теме «Ряды динамики». Задача № 5 по теме «Индексы». Список источников. Статистическая совокупность и статистический показатель, их роль и значение в экономико-статистических явлениях. Статистическая совокупность – множество социально-экономических объектов или явлений общественной жизни, объединенных некой качественной основой, общей связью, но отличающихся друг от друга отдельными признаками. Пример: совокупность домохозяйств, семей, предприятий, фирм, городов области и т.д. Совокупности могут быть однородными и разнородными. Совокупность однородная, если один или несколько изучаемых существенных признаков ее объектов являются общими для всех единиц. Например, мужской пол, возраст 18-25 лет, малые предприятия, предприятия торговли и т.д. Совокупность разнородная, если в нее входят явления разного типа. Совокупность может быть однородна в одном отношении и разнородна в другом: например, торговые предприятия любого размера (малые, средние, крупные). Единица совокупности – отдельная, первичная, неделимая часть совокупности, обладающая признаками, подлежащими регистрации, и основой ведущегося при обследовании счета. Признак совокупности – качественная особенность единицы совокупности. Например, признаки человека: возраст, пол, образование и т.д.; признаки предприятия: форма собственности, отрасль, численность занятых, эффективность и т.д. Классификация признаков: 1) по характеру выражения - атрибутивные (описательные), - количественные а) альтернативные (принимают только два значения), б) дискретные (принимают только целочисленные значения), в) непрерывные (принимают любые значения), 2) по способу измерения - первичные (измеряются, считаются, взвешиваются…), - вторичные (рассчитываются), 3) по отношению к характеризуемому объекту - прямые (непосредственно присущи объекту), - косвенные (опосредованно присущи объекту), 4) по отношению ко времени - моментные (характеризуют объект в один момент времени), - интервальные (характеризуют результаты процессов за период времени). Важной чертой любой статистической совокупности является наличие вариации – изменение величины либо значения признака при переходе от одной единицы совокупности к другой. Если изменения изучаемого явления происходят в разные периоды времени и носят характер закономерности, то говорят о динамике признака. Статистические закономерности устанавливаются с помощью закона больших чисел: при определенных условиях (наличие вероятностных процессов, независимость, большое число факторов) совместное действие большого числа случайных факторов приводит к результатам практически независящим от случая. В реальной жизни существует сложное сочетание различных совокупностей и их элементов. Так, изучая промышленность, статистика рассматривает ее как совокупность предприятий, но каждое предприятие, в свою очередь, — это совокупность рабочих, станков и тому подобное. Базой изучения конкретной статистической закономерности является и совокупность, элементы которой - носители характерных для этой закономерности черт. Совокупность - не механическое объединение элементов, а упорядоченная система, каждый элемент которой представляет собой единство общего и единичного, необходимое и случайного. Необходимость выступает как атрибут общего и оказывается устоявшимися свойствами элементов. Эти свойства обусловлены воздействием объективно необходимых условий существования и развития массового явления, а относительно единичных неповторимых свойств, то они является следствием действия случайных для совокупности причин. Статистика применяет не числа, а показатели. Статистический показатель – число, характеризующее ту или иную особенность признака или явления. Основными задачами в этом направлении являются: 1) правильное определение содержания статистического показателя (ВНП, национального дохода, производительности труда и т.п.); 2) разработка методологии подсчета и расчета статистического показателя. Система статистических показателей – совокупность статистических показателей, отражающая взаимосвязи, которые объективно существуют между явлениями. Система статистических показателей охватывает все стороны жизни общества на различных уровнях: − страны – макроуровень; − региона – мезоуровень; − предприятий, фирм, объединений, семей, домохозяйств – микроуровень. Количество и качество выступают в статистике как две стороны единого. Количество всегда имеет качественную определенность. Именно в этом состоит познавательное значение статистического показателя, который представляет собой количественно-качественную характеристику социально-экономических процессов и явлений в условиях конкретного места и времени. Система статистических показателей – это совокупность взаимосвязанных показателей, объективно отражающая существующие между явлениями взаимосвязи, она охватывает все стороны жизни общества как на макроуровне (страна, регион), так и на микроуровне (отдельное предприятие, фирма, объединение, домохозяйство, семья и т.д.). Показатели в системе могут быть связаны как жестко детерминированной связью (связь основных фондов, числа работников и объема продукции предприятия), так и стохастической связью (зависимость урожайности отдельной культуры от количества внесенных удобрений – с увеличением количества внесенных удобрений урожайность растет в целом, в то время как на отдельных участках посевного клина, ввиду действия других факторов, может наблюдаться даже ее снижение). Система статистических показателей имеет особенности: они носят исторический характер – меняются условия жизни населения, общества, меняются и системы статистических показателей; методология расчета статистических показателей непрерывно совершенствуется. Корреляционно-регрессионный анализ статистической связи социально-экономических явлений. Существующие между явлениями формы и виды связей весьма разнообразны по своей классификации. Предметом статистики являются только такие из них, которые имеют количественный характер и изучаются с помощью количественных методов. Метод корреляционно-регрессионного анализа является основным в изучении взаимосвязей явлений. Данный метод содержит две свои составляющие части - корреляционный анализ и регрессионный анализ. Корреляционный анализ - это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Регрессионный анализ - это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами. Корреляционный метод анализа решает две задачи: установление факта наличия связи и измерение тесноты корреляционной связи по эмпирическим данным. Есть ряд методов выявления связи: приведение параллельных рядов данных, графический, метод аналитической группировки и метод корреляционной таблицы – это специальная комбинационная таблица в которой проведена группировка по двум признакам по факторному и результативному. Концентрация частот около диагонали матрицы свидетельствует о прямой связи, а концентрация частот около побочной диагонали о наличии обратной связи между признаками. В статистике различают: парную корреляцию (взаимосвязь между двумя признаками); частная корреляция (когда рассматривается зависимость между результативными признаками и одним из факторных при фиксированном значении всех остальных факторных признаков); множественная корреляция (зависимость между результативным и 2 или более факторных признаков). Для измерения тесноты связи используется специальный коэффициент, который количественно выражает тесноту связи. Теснота корреляционной связи может быть измерена эмпирическим корреляционным отношением, когда межгрупповая дисперсия характеризует отклонение групповых средних результативного признака от общей средней. Задачи регрессионного анализа – выбор типа модели, установление степени влияния независимых переменных на зависимую и определение расчётных значений зависимости переменной. Для линейной связи вычисляется линейный коэффициент корреляции (показывает направление связи). Коэффициент корреляции может изменятся от -1 до +1. Если значение отрицательно, то связь обратная (с возрастанием факторного признака результат уменьшается). При любой форме связи можно воспользоваться коэффициентом Фехнера. Он основан на сравнении знаков отклонений отдельных значений признаков от средней. Также при любой форме связи можно исчислить теоретическое корреляционное отношение. Данный показатель следует рассчитывать после того, как установлена форма связи и рассчитано уравнение регрессии. Теоретическое корреляционное отношение изменяется от 0 до 1, чем ближе к 1 тем теснее связь. Также для всех форм связи можно рассчитать индекс корреляции (измеряет тесноту связи). Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции. Задача №1 по теме «Статистическая сводка и группировка статистических данных». На основании следующих данных проведите аналитическую группировку по среднесписочной численности работников, разделив всю совокупность предприятий на три группы.По каждой группе рассчитайте объем продукции в среднем на одно предприятие.Результаты оформите в виде таблицы и сделайте соответствующие выводы.
Решение. Проведем ранжирование ряда по среднесписочной численности работников. Таблица 1 - Ранжированный ряд распределения предприятий по среднесписочной численности работников, чел.
Ранжированный ряд изобразим графически (рис. 1). 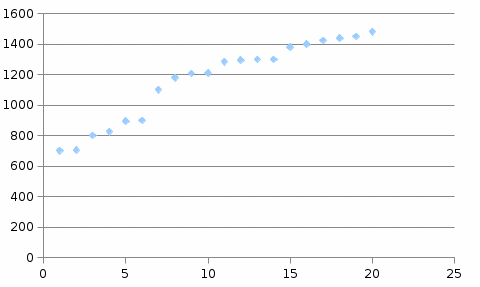 Рисунок 1 - Ранжированный ряд распределения предприятий по среднесписочной численности работников, чел. Данные группируются по признаку-фактору. Затем по каждой группе рассчитывается среднее значение. Задача состоит в том, чтобы увидеть, есть связь между признаками или нет; прямая связь или обратная; линейная или нелинейная. Тогда ширина интервала составит: Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию. Таблица 2 - Интервальный ряд распределения
|
