курсовая. Контрольная работа По дисциплине "Страхование" Страхование граждан от несчастных случаев Выполнил студент Воронин Д. В
 Скачать 1.82 Mb. Скачать 1.82 Mb.
|
|
Размещено на http://www.allbest.ru/ Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования "Нижегородский государственный архитектурно-строительный университет" Кафедра Организации и экономики строительства Контрольная работа По дисциплине "Страхование" Страхование граждан от несчастных случаев Выполнил студент: Воронин Д.В. Проверил преподаватель: Шевченко Ж.А. Нижний Новгород 2017 Содержание Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 1 Страховщик производит страхование граждан от несчастных случаев. Вероятность наступления риска P=0,05, средняя страховая сумма 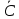 =3,3 тыс. руб., среднее страховое обеспечение =3,3 тыс. руб., среднее страховое обеспечение 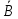 =2,1 тыс. руб., количество договоров =2,1 тыс. руб., количество договоров 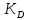 =1500. Доля нагрузки в тарифной ставке =1500. Доля нагрузки в тарифной ставке 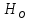 =29%, средний разброс страхового обеспечения R=0,9 тыс. руб., гарантия безопасности =29%, средний разброс страхового обеспечения R=0,9 тыс. руб., гарантия безопасности 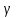 =0,95. Определить: тарифную ставку со 100 руб. страховой суммы (брутто-ставку). =0,95. Определить: тарифную ставку со 100 руб. страховой суммы (брутто-ставку).Дано: P=0,05 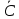 =3,3 тыс. руб. =3,3 тыс. руб.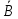 =2,1 тыс. руб. =2,1 тыс. руб.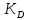 (n)=1500 (n)=1500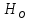 =29% =29%R=0,9 тыс. руб. 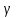 =0,95 =0,95Решение: 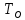 = =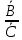 *P*100 *P*100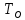 = =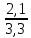 *0,05*100=3,18 руб. *0,05*100=3,18 руб.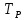 = =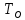 *A* *A*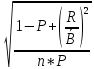 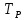 =3,18*1,645* =3,18*1,645*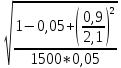 =5,23* =5,23*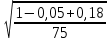 =0,64 руб. =0,64 руб.3) 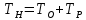 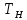 =3,18+0,64=3,82 руб. =3,18+0,64=3,82 руб.4) 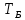 = = 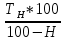 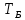 = = 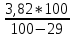 =5,38 руб. со 100 руб. страховой суммы. =5,38 руб. со 100 руб. страховой суммы.Задача 2 Произвести расчет брутто-ставки на дожитие по договору страхования человека в возрасте 30 лет (x=30) на срок 11 лет (n=11) со страховой суммы 100 руб. Доля нагрузки в структуре тарифа 25% (H=25%), процентная ставка в долях единицы 0,27. Дано: x=30лет; n=11лет; H=25%; i=0,27. Определить нетто ставку.
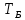 = = 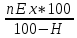 ; ; 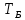 = = 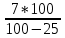 = = 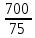 = 9,33 руб. со 100 руб. страховой суммы. = 9,33 руб. со 100 руб. страховой суммы.Задача 3 Рассчитайте единовременную нетто-ставку со 100 руб. страховой суммы по страхованию на дожитие, используя коммутационные числа. Данные для расчета. Возраст страхователя – 43 года. Срок страхования – 10 лет. Коммутационные числа: 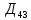 = 1501,66; = 1501,66; 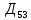 = 539,22. = 539,22.Дано: x – 43 года. n – 10 лет. 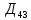 = 1 501,66. = 1 501,66.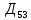 = 539,22. = 539,22.Решение: nЕx = 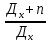 *100; *100; 10Е43 = 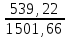 *100 = 35,91 руб. со 100 руб. страховой суммы. *100 = 35,91 руб. со 100 руб. страховой суммы.Задача 4 Страховщик заключает договор имущественного страхования. Вероятность наступления страхового случая P = 0,08. Средняя страховая сумма 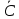 = 95 тыс. руб. Среднее страховое возмещение = 95 тыс. руб. Среднее страховое возмещение 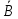 = 77 тыс. руб. Количество договоров = 77 тыс. руб. Количество договоров 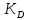 = 3200. Доля нагрузки в структуре тарифа = 3200. Доля нагрузки в структуре тарифа 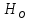 = 35%, гарантия безопасности = 35%, гарантия безопасности 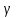 = 0,95. Данные о разбросе возможных страховых возмещений при наступлении страхового случая отсутствуют. = 0,95. Данные о разбросе возможных страховых возмещений при наступлении страхового случая отсутствуют.Дано: P = 0,08. 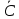 = 95 тыс. руб. = 95 тыс. руб.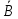 = 77 тыс. руб. = 77 тыс. руб.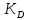 (n)= 3 200. (n)= 3 200.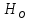 = 35%. = 35%.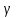 = 0,95. = 0,95.Решение: 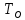 = = 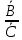 *P*100 *P*100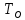 = = 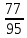 *0,08*100 = 6,48 руб. *0,08*100 = 6,48 руб.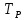 = 1,2* = 1,2*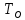 *A* *A*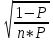 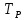 = 1,2*6,48*1,645* = 1,2*6,48*1,645*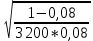 = 0,77 руб. = 0,77 руб.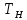 = = 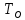 + +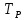 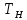 = 6,48+0,77=7,25 руб. = 6,48+0,77=7,25 руб.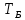 = = 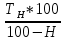 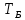 = = 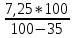 = = 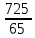 = 11,15 руб. со 100 руб. страховой суммы. = 11,15 руб. со 100 руб. страховой суммы.Задача 5 Определите прогнозируемую убыточность страховой суммы на следующий, после 5 лет, шестой год и рассчитайте тарифную ставку, используя отчетные пятилетние показатели страховой суммы и страхового возмещения. Для проведения расчетов используют данные страховой статистики (табл. 1). Гарантия безопасности 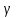 = 0,84. Доля нагрузки в структуре тарифа = 0,84. Доля нагрузки в структуре тарифа 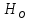 = 35%. = 35%.Таблица 1
Расчет: 4 колонка = 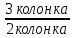 *100 *100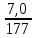 *100 = 3,95; *100 = 3,95; 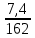 *100 = 4,57; *100 = 4,57; 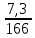 *100 = 4,40; *100 = 4,40; 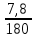 *100 = 4,33; *100 = 4,33; 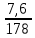 *100 = 4,27 *100 = 4,276 колонка = 4 колонка* 5 колонка 3,95*1 = 3,95; 4,57*2 = 9,14; 4,40*3 = 13,2; 4,33*4 = 17,32; 4,27*5 = 21,35 7 колонка =  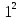 = 1; = 1; 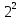 = 4; = 4; 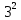 = 9; = 9; 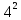 = 16; = 16; 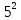 = 25 = 258 колонка: 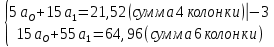 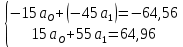 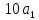 = 0,4 = 0,4 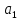 = = 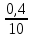 = 0,04 = 0,04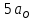 +15*0,04 = 21,52 +15*0,04 = 21,52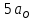 +0,6 = 21,52 +0,6 = 21,52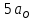 = 20,92 = 20,92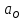 = = 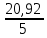 = 4,18 = 4,18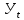 = = 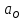 + +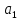 *t *t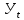 = 4,18+0,04*1 = 4,22 = 4,18+0,04*1 = 4,22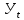 = 4,18+0,04*2 = 4,26 = 4,18+0,04*2 = 4,26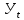 = 4,18+0,04*3 = 4,3 = 4,18+0,04*3 = 4,3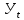 = 4,18+0,04*4 = 4,34 = 4,18+0,04*4 = 4,34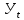 = 4,18+0,04*5 = 4,38 = 4,18+0,04*5 = 4,389 колонка = 8 колонка – 4 колонка 4,22-3,95 = 0,27 4,26-4,57 = -0,31 4,3-4,40 = -0,1 4,34-4,33 = 0,01 4,38-4,27 = 0,11 10 колонка =  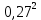 = 0,0729 = 0,0729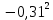 = 0,0961 = 0,0961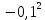 = 0,01 = 0,01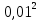 = 0,0001 = 0,0001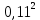 = 0,0121 = 0,0121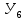 = = 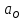 + +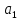 *6 = 4,18+0,04*6 = 4,42 руб. *6 = 4,18+0,04*6 = 4,42 руб.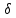 = =  = = 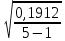 = 0,22 руб. = 0,22 руб.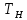 = = 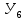 + +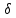 *1,184 = 4,42+0,22*1,184 = 4,68 руб. *1,184 = 4,42+0,22*1,184 = 4,68 руб.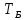 = = 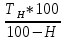 = = 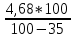 = = 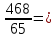 7,2 руб. со 100 руб. страховой суммы. 7,2 руб. со 100 руб. страховой суммы.Задача 6 Заемщик взял кредит в сумме 1 млн. руб. на 1 год. Проценты за кредит составляют - 35% годовых. Предел ответственности страховщика – 73%. Тарифная ставка – 3%. Определить страховую сумму, сумму непогашенного кредита (поэтапно), сумму процентов за пользование кредитом, расчетные тарифные ставки, суммы страховых платежей. По добровольному страхованию риска непогашения кредита, выданного хозяйствующему субъекту, определение страховых платежей производится с помощью специальной справки-расчета (см. табл. 2). Таблица 2 Справка-расчет страховых платежей по добровольному страхованию риска непогашения кредита, выданного хозяйствующему субъекту
Расчет: 5 колонка: 2 колонка = 1000; 1000-400 = 600; 600-300 = 300; 300-300 = 0 6 колонка = 5 колонка* 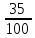 * *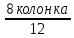 1000* 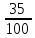 * *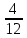 = 115,5; 600* = 115,5; 600*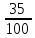 * *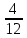 = 69,3; 300* = 69,3; 300*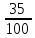 * *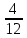 = 34,65 = 34,6510 колонка = 7 колонка* 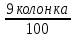 1115,5* 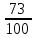 = 814,32; 669,3* = 814,32; 669,3*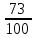 = 488,59; 334,65* = 488,59; 334,65*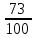 = 244,29 = 244,2912 колонка = 11 колонка* 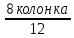 3* 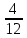 = 1 тарифный страховой прогнозируемый убыточность = 1 тарифный страховой прогнозируемый убыточность13 колонка = 10 колонка* 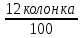 814,32* 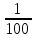 = 8,14 = 8,14488,59* 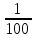 = 4,89 = 4,89244,29* 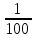 = 2,44 = 2,44Задача 7 Необходимо выбрать наименее убыточный регион. Критерием выбора является минимальная величина следующих показателей страхования: частота страховых событий, коэффициент кумуляции риска, убыточность страховой суммы, тяжесть ущерба. Данные для расчета. В регионе А число застрахованных объектов n = 6 000 единиц; страховая сумма застрахованных объектов С = 80 млн. руб.; число пострадавших объектов m = 3 000 единиц; число страховых случаев l =1 850 единиц; страховое возмещение B=11,3 млн. руб. В регионе Б соответственно n=19 000 единиц; С = 105 млн. руб.; m= 7 000 единиц; l= 5 200 единиц; В = 25 млн. руб.
Решение: 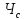 = = 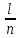 *100 *100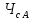 = = 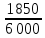 *100 = 30,83 ед.; *100 = 30,83 ед.; 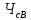 = = 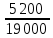 *100 = 27,37 ед. *100 = 27,37 ед.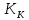 = = 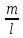 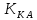 = = 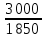 = 1,62 ед.; = 1,62 ед.; 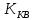 = = 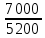 = 1,35 ед. = 1,35 ед.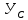 = = 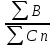 *100 *100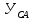 = = 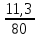 *100 = 14,13 руб.; *100 = 14,13 руб.; 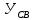 = = 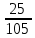 *100 = 23,81 руб. *100 = 23,81 руб.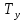 = = 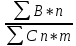 *100 *100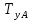 = = 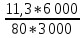 *100 = 28,25 %; *100 = 28,25 %; 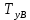 = = 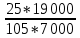 *100 = 64,63 %. *100 = 64,63 %.Вывод: Так как по всем показателям результат 50/50 , делаем вывод по показателю тяжести ущерба. Исходя из этого, регион А является наименее убыточным, чем регион В. Задача 8 Рассчитать показатели страховой статистики при страховании от огня. Данные для расчета. Застраховано рисков – 800, число пожаров – 48, число горевших строений – 85, страховая сумма 17,1 млн. руб., уплачено возмещений по всем пожарам 6,9 млн. руб., средний горевший риск 0,5 млн. руб., средний застрахованный риск 0,9 млн. руб.
Задача 9 Используя коэффициент Коньшина, выберите наиболее финансово устойчивую страховую операцию. Исходные данные для расчета. По страховой операции №1: количество договоров страхования – 15000, средняя тарифная ставка – 0,006 руб. с 1 руб. страховой суммы. По страховой операции №2: количество договоров страхования – 13000, средняя тарифная ставка – 0,0064 руб. с 1 руб. страховой суммы.
Решение: К= 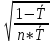 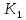 = = 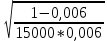 = 0,105; = 0,105; 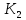 = = 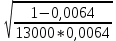 = 0,109 = 0,109Вывод: Финансовая устойчивость страховых операций выше по операции №1, так как в операции №1 коэффициент меньше, чем в операции №2. Задача 10 Используя коэффициент финансовой устойчивости страхового фонда, необходимо выбрать наиболее финансово устойчивую страховую компанию. Исходные данные для расчета. Страховая компания А имеет страховых платежей 4,1 млн. руб. Остаток средств в запасном фонде на конец тарифного периода 0,5 млн. руб., выплаты страхового возмещения 3,2 млн. руб., расходы на ведение дела 0,33 млн. руб. Страховая компания Б имеет страховых платежей 2,2 млн. руб. Остаток средств в запасном фонде на конец тарифного периода 1,4 млн. руб., выплаты страхового возмещения 1,5 млн. руб., расходы на ведение дела 0,28 млн. руб.
Решение: 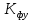 = = 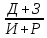 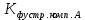 = = 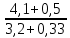 = = 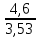 = 1,30 млн. руб.; = 1,30 млн. руб.; 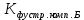 = = 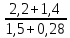 = = 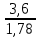 = 2,02 млн. руб. = 2,02 млн. руб.Вывод: Наиболее финансово устойчивой компанией является страховая компания Б, так как коэффициент финансовой устойчивости у страховой компании Б больше, чем у страховой компании А. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

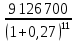
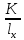
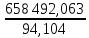
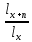
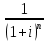
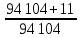
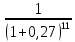 1 метод:
1 метод: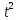
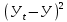 Годы
Годы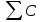
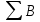
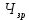
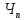
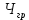
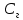
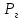
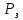
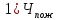
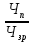
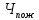
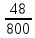
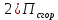
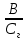
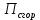
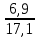
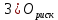
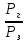
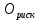
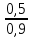
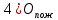
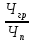
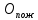
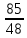
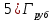
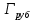 Дано:
Дано: