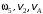Контрольная. Контрольная работа по дисциплине Теоретическая механика Вариант 38 Выполнил ст гр. Гд(ГО)з20 (группа)
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное образовательное учреждение высшего образования «Забайкальский государственный университет» (ФГБОУ ВО «ЗабГУ») Факультет Горный Кафедра Открытые горные работы КОНТРОЛЬНАЯ РАБОТА по дисциплине: «Теоретическая механика» Вариант № 38 Выполнил ст. гр. ГД(ГО)з-20 (группа) . Филинов А.С. . (фамилия, инициалы) Проверил к.п.н. доцент Мурашко С.В. (должность, ученая степень, звание, фамилия, инициалы) Чита 2023 Контрольная работа Вариант 38 (схема 3, вариант данных 8) Задания С1, К2, Д1, Д4 Задание С1 Определение реакций опор твёрдого тела На жёсткую ломаную раму (см. рис.1.4) действуют пара сил с моментом 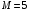 кН·м, распределённая нагрузка q и сила Р. Размеры элементов конструкции, величина, направление и точка приложения силы Р, а также закономерность распределенной нагрузки, её максимальные значения и участок действия принять согласно табл.1.1. Определить реакции в опорах, если кН·м, распределённая нагрузка q и сила Р. Размеры элементов конструкции, величина, направление и точка приложения силы Р, а также закономерность распределенной нагрузки, её максимальные значения и участок действия принять согласно табл.1.1. Определить реакции в опорах, если 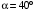 , , 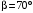 . .Исходные данные:  Рис.1.4
Решение 1. Рассмотрим равновесие рамы. Проведем координатные оси 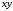 и изобразим действующие на раму силы (рис.1): заданные силу и изобразим действующие на раму силы (рис.1): заданные силу  , пару сил с моментом , пару сил с моментом 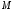 . Равномерно распределенную нагрузку . Равномерно распределенную нагрузку  заменяем равнодействующей сосредоточенной силой заменяем равнодействующей сосредоточенной силой 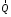 , точка приложения которой расположена на расстоянии, равном , точка приложения которой расположена на расстоянии, равном 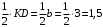 м (от точки D). м (от точки D). При этом численно 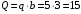 кН. кН.Изображаем реакции связей 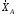 , ,  , , 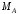 (реакцию жесткой заделки А изображаем двумя составляющими вдоль осей координат и реактивным моментом). (реакцию жесткой заделки А изображаем двумя составляющими вдоль осей координат и реактивным моментом).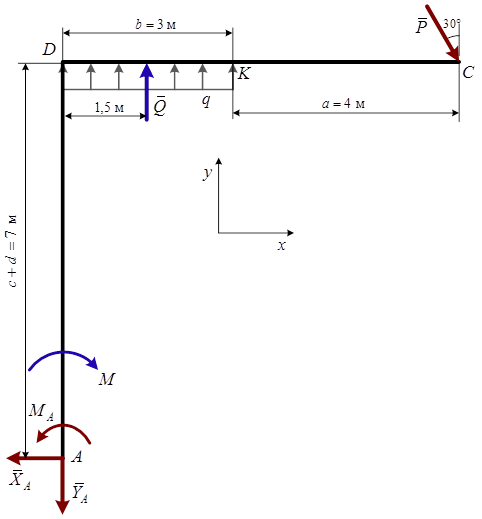 Рис.1. Расчетная схема конструкции Для полученной плоской системы сил составляем три уравнения равновесия. При вычислении момента силы  относительно точки А воспользуемся теоремой Вариньона, то есть мысленно разложим силу относительно точки А воспользуемся теоремой Вариньона, то есть мысленно разложим силу  на составляющие на составляющие 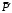 , ,  ( (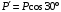 , , 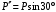 ) и учтем, что ) и учтем, что  . В результате будем иметь: . В результате будем иметь: , ,  ; (1) ; (1)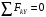 , , 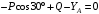 ; (2) ; (2)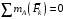 , , 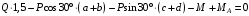 . (3) . (3)Решаем систему уравнений (1)–(3) и находим реакции. Из уравнения (1) находим 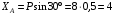 кН. кН.Из уравнения (2) получаем  кН. кН.Из уравнения (3) будем иметь   кН·м. кН·м.Для проверки правильности полученных результатов составим и решим проверочное уравнение равновесия в форме моментов всех сил относительно точки K. 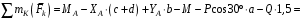 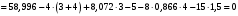 . .Следовательно, реакции определены правильно. Ответ: 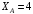 кН; кН; 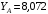 кН; кН; 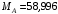 кН·м. кН·м.Задание К2 Кинематический анализ плоского механизма Механическая система в момент времени t занимает положение согласно рис.2.9. Определить кинематические параметры согласно табл. 2.2 и показать их направление на чертеже, если в момент t угловая скорость одного из элементов представлена как 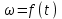 . При выборе исходных данных из табл.2.2 ω1, ω2, ω3 при их положительном значении считать вращение по часовой стрелке, при отрицательном значении – против часовой стрелки, значение ω1 принимать . При выборе исходных данных из табл.2.2 ω1, ω2, ω3 при их положительном значении считать вращение по часовой стрелке, при отрицательном значении – против часовой стрелки, значение ω1 принимать 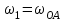 . .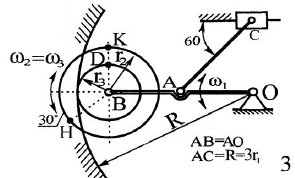
Решение 1. Определяем скорость точки Н. Механическая система состоит из четырёх тел, совершающие следующие движения: тело 1 неподвижно, к нему присоединено водило ОАВ, вращающееся вокруг оси, проходящей через точку О, колесо 2 с двумя ободами, шатун АС, совершающий плоское движение, и ползун С, который перемещается поступательно вдоль своих направляющих. Чтобы найти скорость точки Н 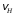 необходимо знать угловую скорость тела 2 необходимо знать угловую скорость тела 2 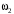 , которому принадлежит эта точка, и положение МЦС тела 2. Угловая скорость , которому принадлежит эта точка, и положение МЦС тела 2. Угловая скорость 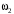 задана в условии задачи. МЦС тела 2 будет находиться в точке контакта поверхностей тела 1 и 2 – точке задана в условии задачи. МЦС тела 2 будет находиться в точке контакта поверхностей тела 1 и 2 – точке  . Тогда искомая скорость точки Н будет равна . Тогда искомая скорость точки Н будет равна , ,где 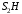 – расстояние от точки Н до МЦС – расстояние от точки Н до МЦС  . .Из треугольника 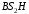 по теореме косинусов имеем по теореме косинусов имеем 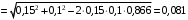 м. м.Тогда 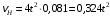 . (1) . (1)Точка  принадлежит колесу 2(3), поэтому ее скорость будет равна принадлежит колесу 2(3), поэтому ее скорость будет равна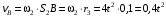 . .Точка В принадлежит также водилу ОАВ, которое вращается с угловой скоростью  вокруг оси, проходящей через точку О. Следовательно, вокруг оси, проходящей через точку О. Следовательно,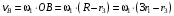 , ,откуда найдем угловую скорость водила 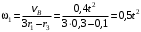 . .2. Определение угловой скорости шатуна 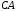 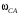 . .Для определения угловой скорости 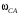 необходимо знать скорость какой-либо точки звена необходимо знать скорость какой-либо точки звена 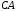 и положение его мгновенного центра скоростей и положение его мгновенного центра скоростей  . Такой точкой является точка А, которая лежит в середине водила и скорость которой равна . Такой точкой является точка А, которая лежит в середине водила и скорость которой равна . .Направлен вектор скорости 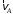 перпендикулярно отрезку ОА в сторону вращения кривошипа (рис.3). перпендикулярно отрезку ОА в сторону вращения кривошипа (рис.3).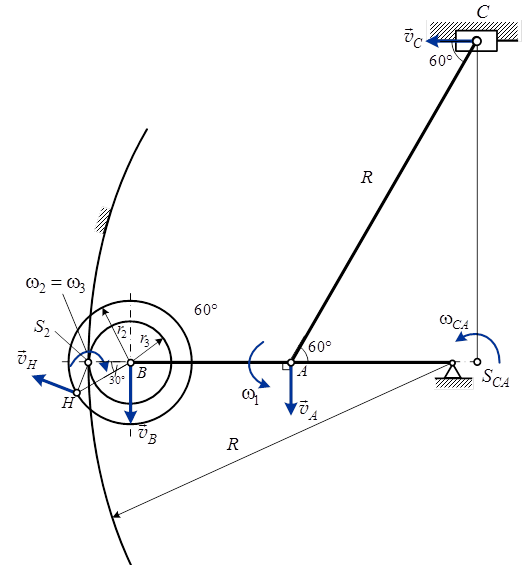 Рис.3. Расчетная схема для определения скоростей и ускорений Далее рассмотрим точку С. Эта точка принадлежит шатуну СА, угловую скорость которого надо определить. Она же принадлежит одновременно ползуну  , который движется поступательно в горизонтальном направлении. , который движется поступательно в горизонтальном направлении.Далее через точки A и С проведем прямые, перпендикулярные направлениям векторов скоростей 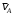 и и 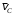 ( ( , , 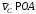 ) и на пересечении получим мгновенный центр скоростей стержня СА – точку ) и на пересечении получим мгновенный центр скоростей стержня СА – точку  . Полученный треугольник . Полученный треугольник 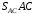 является прямоугольным, в котором отрезок является прямоугольным, в котором отрезок  равен равен м. м.Далее находим искомую угловую скорость звена СА:  . (2) . (2)3. Определяем ускорение точки  согласно векторному уравнению согласно векторному уравнению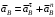 , ,где его касательная и нормальная составляющие равны 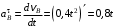 ; ; . .Тогда 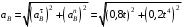 . (3) . (3)4. Угловое ускорение  определим как определим как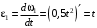 . (4) . (4)Определив кинематические зависимости между точками и телами механической системы, найдем искомые величины при заданном моменте времени 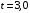 с, используя выражения (1)–(4): с, используя выражения (1)–(4): м/с; м/с;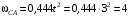 с-1; с-1;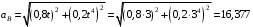 м/с2; м/с2;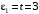 с-2. с-2.Ответ: 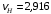 м/с; м/с; 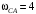 с-1; с-1; 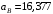 м/с2; м/с2; 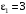 с-2 с-2Задание Д1 Интегрирование дифференциальных уравнений движения материальной точки, находящиеся под действием постоянных сил Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом, в течение τ с. Его начальная скорость 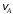 . Коэффициент трения скольжения тела по плоскости равен f. В точке В тело покидает плоскость со скоростью . Коэффициент трения скольжения тела по плоскости равен f. В точке В тело покидает плоскость со скоростью 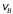 , описывает траекторию , описывает траекторию  и попадает в точку С плоскости BC или BD со скоростью и попадает в точку С плоскости BC или BD со скоростью 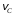 , находясь в полете Т с. , находясь в полете Т с.Исходные данные и параметры, которые требуется определить, взять из табл.3.2 и рис. 3.8. Считать  и и 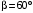 . При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать. . При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать.Исходные данные: 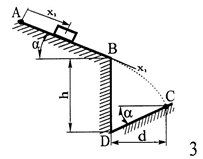 Рис.3.8 Дано:  ; ; 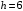 м; м; 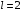 м; м;  с; с; 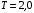 с. с.Найти: 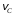 , ,  , , 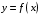 . .Решение Рассмотрим вначале движение тела от точки В к точке С (рис.1). На тело действует сила тяжести 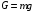 . Дифференциальные уравнения движения тела по осям координат будут: . Дифференциальные уравнения движения тела по осям координат будут: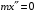 ; ; 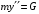 . .Интегрируем первое уравнение. Тогда получим 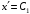 ; ;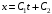 . .Постоянные интегрирования  определим, используя начальные условия задачи: при определим, используя начальные условия задачи: при 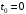 , ,  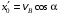 . Тогда будем иметь . Тогда будем иметь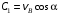 ; ; 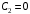 . .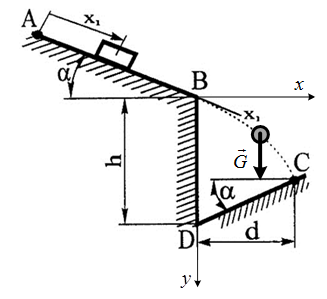 Рис.1. Расчетная схема к заданию Д1 Таким образом, уравнения движения тела в горизонтальном направлении  ; (1) ; (1)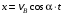 . (2) . (2)Интегрируя уравнение 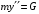 , получим , получим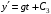 ; ;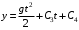 . .Начальные условия 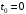 , , 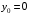 ; ; 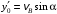 , следовательно, , следовательно, 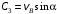 , , 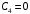 и уравнения движения тела в вертикальном направлении и уравнения движения тела в вертикальном направлении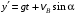 ; (3) ; (3)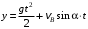 . (4) . (4)Предварительно из уравнений (2) и (4) определим скорость тела в точке В. Для этого примем 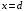 , ,  и и 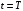 . Тогда получим . Тогда получим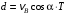 ; (5) ; (5)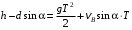 . (6) . (6)Подставляя (5) в (6), получим 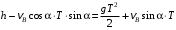 откуда находим 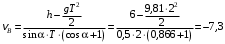 м/с. м/с.Знак минус указывает на то, что заданное в условии задачи движение тела по пути А–В–С не осуществимо. Изменим исходные данные и примем время полета теле на участке ВС равным 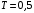 с. Тогда получим с. Тогда получим м/с. м/с.Уравнение траектории движения тела найдем, исключив параметр 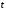 из уравнений движения. Определив из уравнений движения. Определив 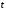 из уравнения (2) и подставив в уравнение (4), получим уравнение параболы: из уравнения (2) и подставив в уравнение (4), получим уравнение параболы: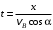 ; ;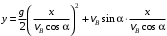 ; ;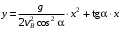 . .Подставив числовые данные, будем иметь  . (7) . (7)Уравнение (7) является искомым уравнением 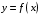 в выбранной системе координат. в выбранной системе координат.Скорость тела при падении в точке С найдем через проекции скорости на оси координат – уравнения (1) и (3):  ; ; 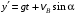 . .Для момента времени 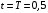 с получим с получим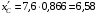 м/с: м/с: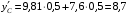 м/с. м/с.Абсолютное значение скорости тела в точке С будет равно  м/с. м/с.2. Для нахождения коэффициента трения скольжения  рассмотрим движение тела на участке АВ (рис.2). рассмотрим движение тела на участке АВ (рис.2). 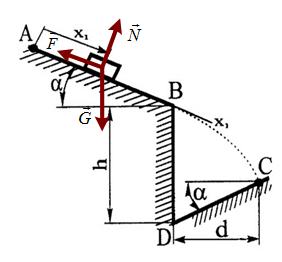 Рис.2. Расчетная схема 2 к заданию Д1 Принимая тело за материальную точку, покажем действующие на него силы: вес  , нормальную реакцию , нормальную реакцию 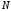 и силу трения скольжения и силу трения скольжения 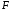 . Составим дифференциальные уравнения движения тела на участке АВ: . Составим дифференциальные уравнения движения тела на участке АВ: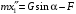 . .Сила трения 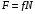 , ,где  . .Таким образом, 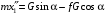 или 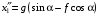 . .Интегрируя дифференциальное уравнение дважды, получим 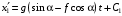 ; ;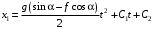 . .Для определения постоянных интегрирования воспользуемся начальными условиями задачи: 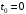 ; ; 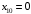 ; ; 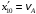 . .Составим уравнения, полученные при интегрировании, для  ; ; 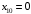 ; ; 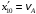 . Находим постоянные: . Находим постоянные: ; ; 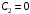 . .Таким образом, уравнения движения тела на участке АВ имеют вид 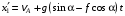 ; ;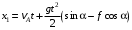 . .Для момента времени 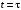 , когда тело покидает участок АВ, , когда тело покидает участок АВ, 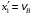 , , 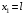 . Таким образом, получаем . Таким образом, получаем ; ;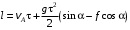 . .Из первого уравнения выражаем скорость 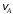 и подставляем во второе уравнение и подставляем во второе уравнение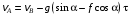 ; ;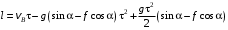 ; ;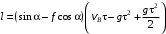 ; ;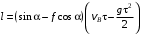 , ,откуда находим искомый коэффициент трения 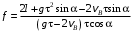 . .Выполняем вычисления 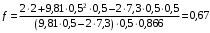 . .Ответ:  м/с; м/с; 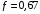 ; ;  . .Задание Д4 Применение теоремы об изменении кинетической энергии к изучению движения механической системы Механическая система (рис 3.16) состоит из грузов 1 и 2, катка 3, шкивов 4 и 5 радиусами R4=0,4м, r4=0,2 м, R5=0,5 м, r5=0,1 м соответственно. Каток считать сплошными однородным цилиндром, а массу шкивов считать распределенной по ободу. Коэффициент трения грузов о плоскость f=0,1. Тела системы соединены друг с другом нитями, участки нитей параллельны соответствующим плоскостям. Под действием силы F=f(t), зависящей от перемещения S точки ее приложения, система приходит в движение из состояния покоя. При движении на шкивы 4 и 5 действуют постоянный момент М1, М2 сил сопротивления соответственно. Определить значение искомой величины в тот момент времени, когда перемещение S станет равным S1. Искомые величины указана в столбце «Найти» таблицы 3.5. Исходные данные:  Рис. 3.16 Таблица 6
Решение 1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 2, 3, 4, 5, соединенных нитями. Изобразим действующие на систему внешние силы: активные 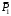 , , 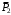 , , 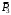 , , 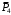 , , 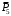 , реакции , реакции  , ,  , , 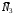 , , 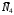 , , 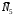 , силы трения , силы трения 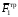 , , 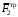 , , 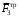 и моменты и моменты 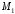 и и  (рис.3). (рис.3).Определим вначале скорость груза 2 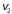 . .Для определения скорости 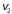 воспользуемся теоремой об изменении кинетической энергии: воспользуемся теоремой об изменении кинетической энергии:2. Определяем  . (2) . (2)Учитывая, что тела 1 и 2 движутся поступательно, тела 4 и 5 вращается вокруг неподвижной оси, а тело 3 совершает плоскопараллельное движение, получим 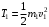 ; ;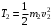 ; ;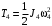 ; ;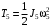 . (3) . (3)Все входящие сюда скорости необходимо выразить через искомую 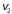 . Для этого предварительно заметим, что точка . Для этого предварительно заметим, что точка 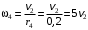 ; ;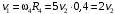 ; ;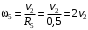 ; ;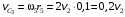 ; ;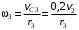 . (4) . (4)Кроме того, входящие в (3) моменты инерции имеют значения: 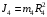 ; ; 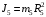 ; ; Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно 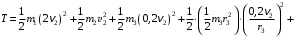 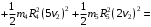 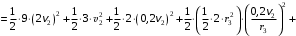 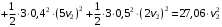 . (6) . (6) Рис.3. Расчетная схема к заданию Д4 3. Далее найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда тело 1 (к нему приложена сила F=f(t))пройдет путь 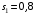 м. Введем обозначения: м. Введем обозначения: Тогда получим 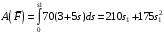 ; ;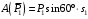 ; ; ; ;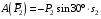 ; ;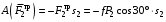 ; ;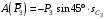 ; ;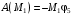 ; ;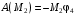 . .Работы остальных сил равны нулю, так как точки, где приложены силы 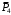 и и 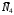 , , 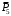 и и 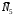 – неподвижны, силы – неподвижны, силы  , , 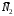 перпендикулярны направлению перемещения соответственно тел 1, 2, а силы перпендикулярны направлению перемещения соответственно тел 1, 2, а силы Величины 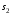 , , 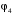 и и  необходимо выразить через заданное перемещение необходимо выразить через заданное перемещение 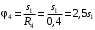 ; ;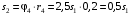 ; ;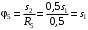 ; ;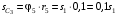 . .При найденных значениях линейных у угловых перемещений для суммы вычисленных работ получим 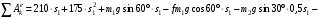  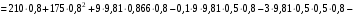  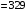 . (7) . (7)Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что 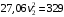 , ,откуда искомая скорость тела 2 будет равна 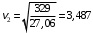 м/с. м/с.Находим остальные требуемые скорости:  рад/с; рад/с; м/с. м/с.Ответ: 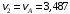 м/с; м/с;  рад/с. рад/с.Список использованной литературы 1. Учебные материалы для студентов заочной формы обучения по теоретической механике. ФГБОУ ВПО «ЗабГУ». 2. Тарг С.М. Теоретическая механика. Методические указания и контрольные задания. М.: Высшая школа, 1989. 3. Никитин Н.Н. Курс теоретической механики. М.: Высшая школа, 1990. 4. Гернет М.М. Курс теоретической механики. М.: Высшая школа, 1987. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

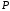 , кН
, кН , м
, м , м
, м , м
, м , м
, м
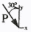
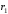 , м
, м , м
, м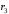 , м
, м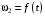 ,
,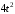
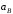 ,
,