Стрельцов 19 ИФЗ. Контрольная работа По дисциплине Теоретические основы электротехники Выполнил студент Факультета итисс стрельцов Е. Н

• Название: Контрольная работа По дисциплине Теоретические основы электротехники Выполнил студент Факультета итисс стрельцов Е. Н
• Дата: 19.02.2022
• Размер: 0.63 Mb.
• Имя файла: Стрельцов 19 ИФЗ.doc
• Тип: Контрольная работа; #367071

Министерство образования Нижегородской области

Государственное образовательное учреждение

высшего образования

Нижегородский государственный инженерно-экономический университет

(ГБОУ ВО НГИЭУ)

Факультет: ИТиСС

Кафедра: «Инфокоммуникационные технологии и системы связи»

Контрольная работа

По дисциплине: «Теоретические основы электротехники»

Выполнил студент:

Факультета ИТиСС

Стрельцов Е.Н

Проверил преподаватель:

Осокин В.Л.

г. Княгинино

2022 г.

Содержание

1.Задача №1………………………………………………………………………..3 2.Задача №2………………………………………………………………………..8 3.Задача №3……………………………………………………………………... 13 4.Задача №4……………………………………………………………………....19 5.Задача №5………………………………………………………………………25 Литература……………………………………………………………………….30

Задача 1

Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии

Для электрической цепи, изображенной на рисунке 1, определить:

1. Токи в ветвях методом преобразований (схему упрощают путем замены участков с параллельным или последовательным соединением эквивалентных элементов).

2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить баланс мощностей.

3. Составить уравнения по первому закону Кирхгофа для узлов схемы. Составить уравнение по второму закону Кирхгофа для любого замкнутого контура, включающего ЭДС Е.

Исходные данные сведены в таблицу 1.

Таблица 1 – Исходные данные

Параметры цепи	9
E, B	140
R1, Ом	8
R2, Ом	13
R3, Ом	9
R4, Ом	14
R5, Ом	10
R6, Ом	15

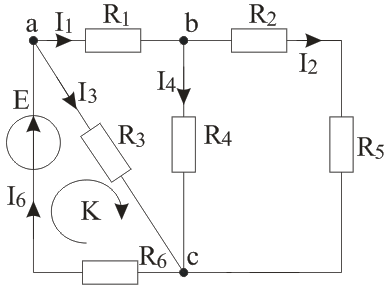Рисунок 1 – Схема цепи

Решение:

1. 
   Определить токи в ветвях методом преобразований (схему упрощают путем замены участков с параллельным или последовательным соединением эквивалентным элементов).
   

Сопротивление последовательно соединенных резисторов R₂ и R₅:

(1)

Схема примет вид, указанный на рисунке 2.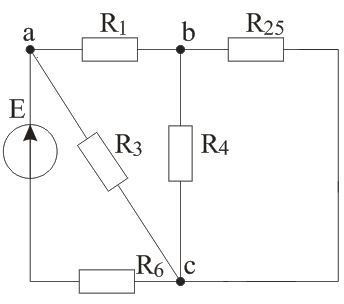



Рисунок 2 – Схема после первого упрощения

Эквивалентное сопротивление параллельно соединенных резисторов R₄ и R₂₅:

(2)

Схема примет вид, указанный на рисунке 3.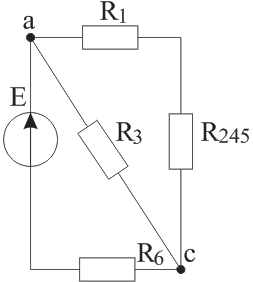



Рисунок 3 – Схема после второго упрощения

Эквивалентное сопротивление последовательно соединенных резисторов R₁ и R₂₄₅:

(3)

Схема примет вид, указанный на рисунке 4.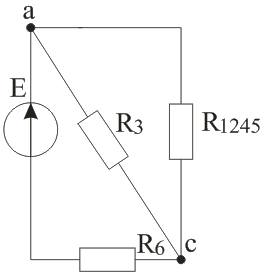



Рисунок 4 – Схема после третьего упрощения

Эквивалентное сопротивление параллельно соединенных резисторов R₃ и R₁₂₄₅:

(4)

Схема примет вид, указанный на рисунке 5.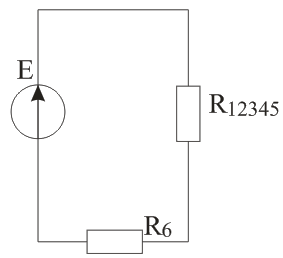



Рисунок 5 – Схема после четвертого упрощения

Эквивалентное сопротивление всей цепи:

(5)

Окончательно упрощенная схема представлена на рисунке 6.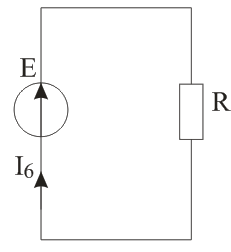



Рисунок 6 – Окончательно упрощенная схема

Ток источника и ток в резисторе R₆ по закону Ома:

(6)

Напряжение на резисторе R₃:

(7)

Ток в резисторе R₃:

(8)

Ток в резисторе R₁ по первому закону Кирхгофа:

(9)

Напряжение на резисторе R₄:

(10)

Ток в резисторе R₄:

(11)

Ток в резисторах R₂ и R₅ одинаков:

(12)

2. 
   Определить мощность, развиваемую источником энергии и мощность потребителей. Проверить баланс мощностей.
   

Мощность источника энергии:

(19)

Мощность потребителей:

(20)

Баланс мощностей:

(21)

Итак, Р_Е=Р_R=935Вт – мощность источника равна мощности потребителей, баланс мощностей соблюден, следовательно, расчет верен.

3. 
   Составить уравнения по первому закону Кирхгофа для узлов схемы. Составить уравнение по второму закону Кирхгофа для любого замкнутого контура, включающего ЭДС Е.
   

Уравнение первого закона Кирхгофа запишем для узлов а, b, c (рисунок 1):

(22)

Уравнение второго закона Кирхгофа запишем для контура К (рисунок 1):

(23)

Подставим числовые данные и проверим первый закон Кирхгофа:

(24)

Как видим, первый закон Кирхгофа соблюден.

Подставим числовые данные и проверим второй закон Кирхгофа:

(25)

Как видим, второй закон Кирхгофа соблюден.

Задача 2

Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.

Для электрической цепи, изображенной на рисунке 7, выполнить следующее:

1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений следует в интегрированном пакете MathCAD.

2. Определить токи в ветвях методом контурных токов.

3. Определить режимы работы активных элементов и составить баланс мощности.

Исходные данные сведены в таблицу 2.

Таблица 2 – Исходные данные

Параметры цепи	9
E1, B	140
E2, B	120
R1, Ом	18
R2, Ом	16
R3, Ом	12
R4, Ом	20
R5, Ом	15
R6, Ом	10

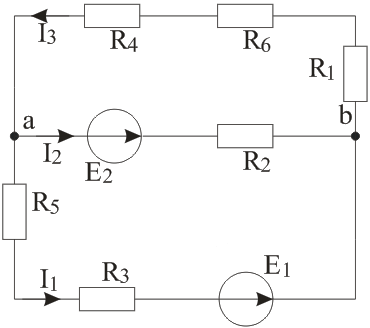Рисунок 7 – Схема цепи

Решение:

1. 
   Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений следует в интегрированном пакете MathCAD.
   

Расчетная схема с выбранными направлениями токов и контуров представлена на рисунке 8.

В схеме 3 неизвестных тока и 2 узла, следовательно, необходимо составить 2–1=1 уравнение по первому закону Кирхгофа и 3–1=2 уравнения по второму закону Кирхгофа.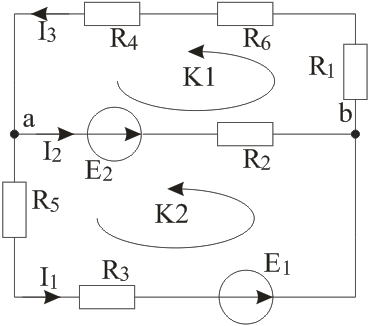



Рисунок 7 – Расчетная схема для применения законов Кирхгофа

В схеме только 2 узла (а и b), поэтому первый закон Кирхгофа выглядит одинаково для любого узла:

(26)

Второй закон Кирхгофа для контуров К1 и К2 соответственно:

(27)

Запишем систему уравнений (26) – (27) в матричной форме, пригодной для решения с помощью Mathcad:

(28)

Подставим числовые данные:

(29)

Решив систему (29) с помощью Mathcad, получим матрицу токов:

(30)

Токи: I₁= 1,28A; I₂=0,913A; I₃=2,2A.

2. 
   Определить токи в ветвях методом контурных токов.
   

Количество уравнений контурных токов:

(31)

где N_B=3 – число ветвей;

N_Y=2 – число узлов;

N_T=0 – число источников тока.

Имеем:

(32)

Выбранные контурные токи указаны на рисунке 8.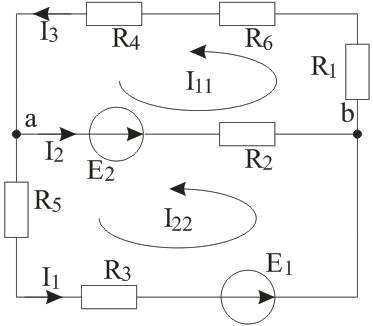



Рисунок 8 – Расчетная схема для применения контурных токов

Уравнения контурных токов:

(33)

Запишем систему в матричной форме для решения ее с помощью Mathcad:

(34)

Подставим числовые данные:

(35)

Решив матричное уравнение (35) с помощью Mathcad, получим значения контурных токов:

(36)

Зная контурные токи, найдем токи в ветвях:

(37)

3. 
   Определить режимы работы активных элементов и составить баланс мощности.
   

Ток I₁ в источнике ЭДС Е₁ направлен в направлении ЭДС этого источника, поэтому источник ЭДС Е₁ работает в режиме генератора энергии.

Ток I₂ в источнике ЭДС Е₂ направлен в направлении ЭДС этого источника, поэтому источник ЭДС Е₂ работает в режиме генератора энергии.
Рассчитываем мощность источников ЭДС:

(38)

Рассчитываем мощность приемников:

(39)

Баланс мощностей:

(40)

Итак, Р_Е=P_R=289Вт, баланс мощностей соблюден, следовательно, расчет верен.

Задача №3. Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии

Для электрической цепи, изображенной на рис. 5, выполнить следующее:

1. Записать систему уравнений для определения токов в ветвях путем непосредственного применения законов Кирхгофа. Решить эту систему уравнений с применением интегрированного пакета MathCAD.

2. Определить токи во всех ветвях методом контурных токов.

3. Выполнить сравнение результатов полученных в п.1 и в п. 2.

4. Составить баланс мощностей.

5. Построить потенциальную диаграмму для любого замкнутого контура, включающего в себя обе ЭДС.

Таблица№3

№ вар	E1, В	r1, Ом	E2, В	r2, Ом	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом	R6, Ом
39	90	2	170	1	6	7	16	21	15	23

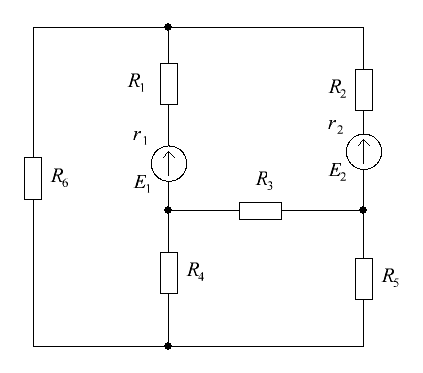Рис. 5
Решение:

1. Составим на основании законов Кирхгофа системы уравнений для расчета токов во всех ветвях схемы.

Выбираем условно-положительные направления токов в ветвях (см. рис. 6)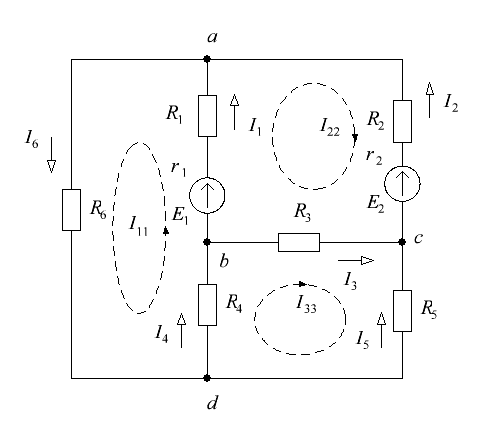



Рис. 6
Схема электрической цепи, изображенная на рис. 2, содержит 4 узла, 6 ветвей с шестью неизвестными токами и 3 независимых контура. Для определения токов в ветвях исходной цепи по законам Кирхгофа необходимо составить уравнения по первому закону, где – количество узлов в цепи; уравнения по второму закону, где – количество независимых контуров.

Составим уравнения по первому закону Кирхгофа для узлов a, b, c; по второму закону Кирхгофа для контуров I, II и III. Направление обхода контуров показано на рисунке.

Выполняем расчет в программе Mathcad: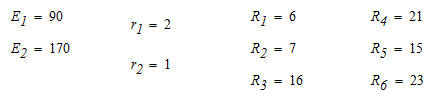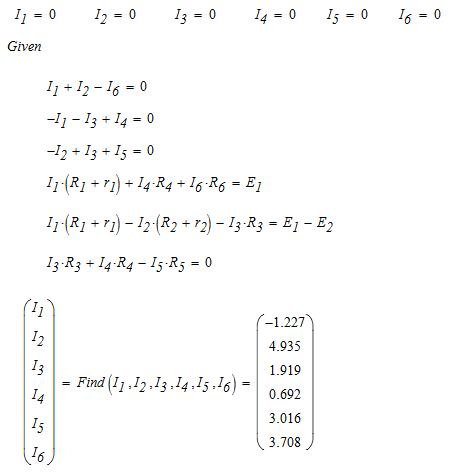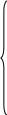




2. Определим токи во всех ветвях методом контурных токов.

Для рассматриваемой двухконтурной цепи система уравнений относительно контурных токов, совпадающих по направлению с обходом контуров, примет вид: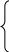

,

,

.

Подсчитаем значения коэффициентов системы:

– собственные сопротивления контуров:

Ом,

Ом,

Ом.

– общие сопротивления контуров:

Ом,

Ом,

Ом;

– контурные ЭДС:

В,

В.

В.

После подстановки численных значений коэффициентов и необходимых преобразований система уравнений примет вид: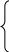

,

,

.

В результате расчета системы уравнений получим:

А, А, А.

В соответствии с принятыми положительными направлениями токов в ветвях вычисляем их значения:

А,

А,

А,

А,

А,

А.

Полученные значения токов совпадают с рассчитанными в п.1.

3. Составим баланс мощностей.

Мощность источников:

Вт.

Мощность потребителей:



Вт.

, следовательно, баланс мощностей выполняется.

4. Для контура, изображенного на рис. 7, рассчитаем и построим потенциальную диаграмму.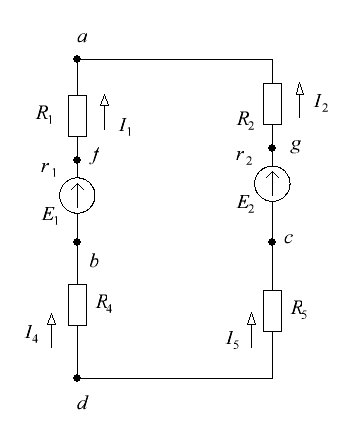



Рис. 7
Определим потенциалы точек цепи, принимая :

В,

В,

В,

В,

В,

В.

Потенциальная диаграмма изображена на рис. 8.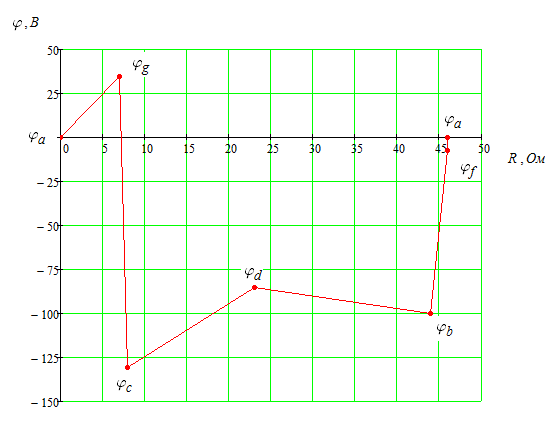



Рис. 8

Задача 4

Расчет неразветвленной линейной цепи синусоидального тока.

Напряжение на зажимах цепи, вариант которой соответствует предпоследней цифре учебного шифра студента и изображенной на рисунке 9, изменяется по закону u=U_msinωt. Амплитудное значение напряжения U_m, значения активных сопротивлений r₁ и r₂ , индуктивностей катушек L₁ и L₂ , емкостей конденсаторов С₁, и С₂ приведены в таблице 3. Частота питающего напряжения f = 50 Гц.

Необходимо:

1.Определить показания приборов, указанных на рисунке 9.

2. Определить закон изменения тока в цепи.

3. Определить закон изменения напряжения между зажимами, к которым подключен вольтметр.

4. Построить векторную диаграмму токов и напряжений.

5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс активной и реактивной мощностей.

6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в цепь для того, чтобы в ней имел место резонанс напряжений.

Таблица 3 – Исходные данные

Параметры цепи	9
Um, B	320
r1, Ом	10
r2, Ом	6
L1, Гн	0,04
L2, Гн	0,01
С1, мкФ	500
С2, мкФ	300

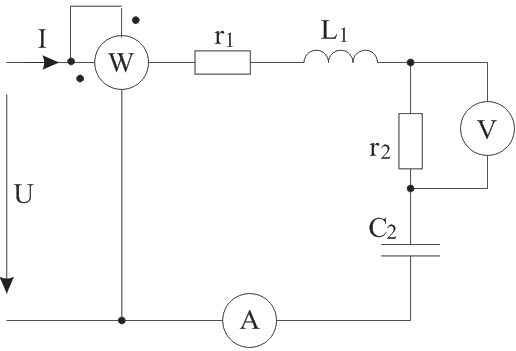Рисунок 9 – Схема цепи
Решение:

1. 
   Определить показания приборов, указанных на рисунке 9.
   

Найдем действующее значение напряжения, приложенного к цепи:

(41)

Активное сопротивление всей цепи:

(42)

Круговая частота питающего напряжения:

(43)

Реактивные сопротивления элементов цепи соответственно:

(44)

Реактивное сопротивление всей цепи:

(45)

Полное сопротивление цепи:

(46)

По закону Ома находим действующее значение тока в цепи:

(47)

По закону Ома находим напряжение на резисторе r₂:

(48)

Активная мощность цепи:

(49)

Показания амперметра А – это действующее значение тока в цепи:

(50)

Вольтметр V измеряет напряжение на резисторе r₂:

(51)

Ваттметр W измеряет активную мощность цепи:

(52)

2. 
   Определить закон изменения тока в цепи.
   

Амплитуда тока цепи:

(53)

Сдвиг фаз между током и напряжением, приложенным к цепи:

(54)

Так как сопротивление цепи носит индуктивный характер, ток I отстает по фазе от напряжения U на угол 7,1°.

Тогда закон изменения тока в цепи, учитывая, что начальная фаза питающего напряжения равна нулю:

(55)

3. 
   Определить закон изменения напряжения между зажимами, к которым подключен вольтметр.
   

Амплитуда напряжения между зажимами, к которым подключен вольтметр:

(56)

Напряжение на активном сопротивлении r₂ совпадает по фазе с током цепи, поэтому начальная фаза напряжения между зажимами, к которым подключен вольтметр, такая же, как у тока i:

(57)

Тогда закон изменения напряжения между зажимами, к которым подключен вольтметр:

(58)

4. 
   Построить векторную диаграмму токов и напряжений.
   

Для построения векторной диаграммы необходимо найти напряжение на каждом элементе схемы:

(59)

Векторную диаграмму строим, руководствуясь тем, что напряжения на активных сопротивлениях совпадают по фазе с током в цепи, на индуктивности напряжение опережает ток по фазе на 90°, на емкости – отстает по фазе от тока на 90°.

Векторная диаграмма приведена на рисунке 10, масштаб указан там же.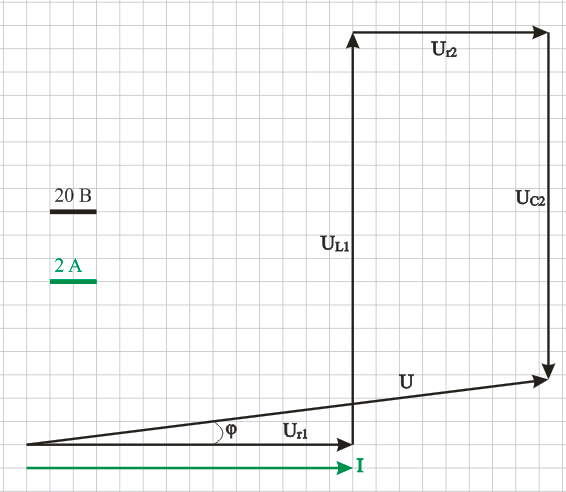



Рисунок 10 – Векторная диаграмма

5. 
   Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс активной и реактивной мощностей.
   

Полная мощность источника:

(60)

Активная мощность источника:

(61)

Реактивная мощность источника:

(62)

Активная мощность приемников:

(63)

Реактивная мощность приемников:

(64)

Полная мощность приемников:

(65)

Итак, Р=P_U=3143Вт – активная мощность приемников равна активной мощности источника, баланс активных мощностей соблюден;

Q=Q_U=393Bap – реактивная мощность приемников равна реактивной мощности источника, баланс реактивных мощностей соблюден.

Расчеты производились в Mathcad – этим объясняется высокая точность совпадения баланса мощностей.

6. 
   Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в цепь для того, чтобы в ней имел место резонанс напряжений.
   

Резонанс напряжений наступает при равенстве нулю реактивной составляющей сопротивления схемы.

Реактивное сопротивление схемы носит индуктивный характер и уже найдено:

(66)

Таким образом, для обеспечения резонанса напряжений, в цепь последовательно с остальными элементами необходимо включить конденсатор с емкостным сопротивлением:

(67)

Тогда реактивное сопротивление цепи будет равно нулю:

(68)

Емкость добавочного конденсатора:

(69)

Задача №5. Расчет разветвленной линейной цепи синусоидального тока

Напряжение на зажимах цепи, схема которой изображена на рис. 12, изменяется по закону . Амплитудное значение тока I_m, значения активных сопротивлений r₁ и r₂, индуктивностей катушекL₁ и L₂, емкостей конденсаторов С₁ и С₂ приведены в таблице №5.

Частота питающего напряжения Гц.

Необходимо:

1. Определить показания приборов, указанных на рис. 12.

2. Определить закон изменения тока в цепи.

3. Определить закон изменения напряжения между зажимами, к которым подключен вольтметр.

4. Построить векторную диаграмму токов и напряжений.

5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс активной и реактивной мощностей.

6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в цепь для того, чтобы в ней имел место резонанс токов.

Таблица №5

№ вар	Im, А	R1, Ом	R2, Ом	L1, Гн	L2, Гн	C1, мкФ	C2, мкФ
39	18	3	8	0,02	0,03	500	200

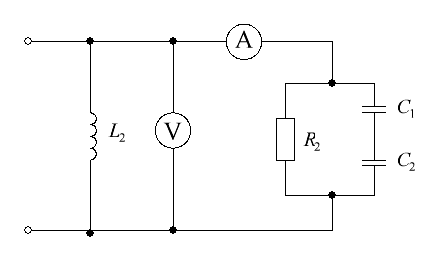Рис. 12

Решение:

1. Определим сопротивления реактивных элементов:

Ом,

Ом,

Ом.

2. Обозначим направления токов в ветвях (см. рис. 13) и определим проводимости ветвей с учетом характера элементов и входную проводимость цепи.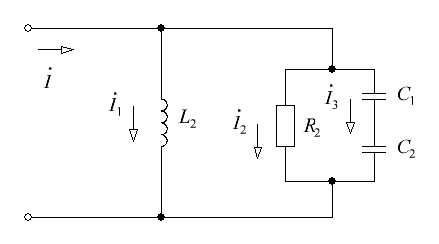



Рис. 13
См,

См,

См,

См.

3. Определим приложенное напряжение:

В,

где А.

4. Вольтметр, подключенный к цепи, покажет действующее значение приложенного напряжения:

В.

5. Определим токи в ветвях с учетом характера элементов через активные и реактивные составляющие:

А,

А,

А.

6. Определим ток, протекающий через амперметр, используя первый закон Кирхгофа, и показание амперметра:

А.

7. Запишем закон изменения напряжения между зажимами, к которым подключен вольтметр:

В.

8. Определим угол сдвига фаз между током и напряжением на входе цепи:

, тогда

, т.е. напряжение опережает ток на угол .

9. Запишем закон изменения тока на входе цепи:

В.

10. Построим векторную диаграмму токов и напряжений (см. рис. 14).

Построение векторной диаграммы начинаем с построения вектора напряжения, который направляем вдоль действительной полуоси. Далее строим векторы токов, руководствуясь следующим: токи в резисторах совпадают по фазе с напряжением, ток в конденсаторе опережает напряжение на 90 градусов, ток в катушке отстает от напряжения на 90 градусов. В результате построения геометрическая сумма векторов токов в параллельных ветвях равна вектору тока на входе цепи.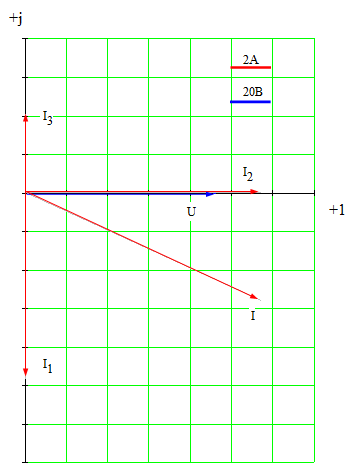



Рис. 14
11. Определим активную, реактивную и полную мощности, потребляемые цепью.

Активная мощность, потребляемая цепью:

Вт.

Реактивная мощность, потребляемая цепью:



вар.

Полная мощность, потребляемая цепью:

ВАр.

12. Определим активную, реактивную и полную мощности источника.

Активная мощность источника:

Вт.

Реактивная мощность источника:

вар.

Полная мощность источника:

ВАр.

13. Таким образом, , , , следовательно, баланс мощностей соблюдается.

14. Определим характер (индуктивность, емкость) и параметры элемента, который должен быть включен в цепь для того, чтобы в ней имел место резонанс токов.

Условием резонанса токов в параллельном контуре является равенство нулю реактивной проводимости цепи. Реактивная проводимость исходной цепи:

См.

Таким образом, для возникновения резонанса токов необходимо подключить конденсатор с реактивной проводимостью: См.

Определим емкость конденсатора:

Ф мкФ.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. 
   Атабеков Г.И. Линейные электрические цепи. – М.: Энергия, 1978. – 592 с.
   
2. 
   Бессонов Л.А. Теоретические основы электротехники: Электрические цепи: Учебник. – 10-е изд. –М.: Гардарики, 2002. – 638 с.
   
3. 
   Буртаев Е.В. «Теоретические основы электротехники» М.: Энергоатомиздат, 1984.
   
4. 
   Данилов И.А., Иванов П.М. Общая электротехника с основами электроники. – М., 1983.
   
5. 
   Евдокимов Ф.Е. «Теоретические основы электротехники». – М.: Высшая школа, 2001.
   
6. 
   Зайчик М. Ю. «Сборник задач и упражнений по теоретической электротехнике»: Учеб. Пособие для техникумов. – 6-е изд. Перераб. и доп. – М.: Энергоатомиздат. 1988.
   
7. 
   Попов В.С. «Теоретическая электротехника»: Для учащихся техникумов.- М.: Энергоатомиздат, 1990.
   
8. 
   Теоретические основы электротехники: Методические указания и контрольные задания для студентов тех. спец. вузов/ Л.А. Бессонов, И.Г. Демидова, М.Е. Заруди и др. – 3-е изд., испр. – М.: Высшая школа, 2003. – 159 с.